连续分布：

1. 经验分布（empirical distribution）：基于观察，样本有限。对应的是连续分布（continuous distribution），更为常见。
2. 指数分布（exponential distribution）：观察一系列事件之间的间隔时间（interarrival time）。若事件在每个时间点发生的概率相同，那么间隔时间的分布就近似于指数分布。\(\begin{align} CDF(x) = 1 - e^{-\lambda x} \end{align}\)。指数分布的均值：1/λ，中位数是log(2)/λ。
3. 判断分布是否符合指数分布：画出取对数后的互补累积分布函数（Complementary CDF，CCDF）：1 - CDF(x)， \(\begin{align} 1-CDF(x) = e^{-\lambda x} \end{align}\)，取对数, \(\begin{align} logy = -\lambda x \end{align}\)，在y取对数之后，整体是一条直线（斜率为-λ）。
4. 帕累托分布：描述财富分布情况。CDF: \(\begin{align} CDF(x) = 1 - {\frac{x}{x_m}}^{-\alpha} \end{align}\)，其中xm是最小值。比如城镇人口分布。
5. 判断分布是否符合帕累托分布：对两条数轴都取对数后，其CCDF应该基本上是一条直线。\(\begin{align} logy ≈ −\alpha(logx−logx_m) \end{align}\)。
6. 威布尔分布是一个广义上的指数分布，源自故障分析。\(\begin{align} CDF(x) = 1−e^{−(x/λ)k} \end{align}\)。
7. 正太分布（高斯分布）：正态分布的CDF还没有一种准确的表达，最常用的一种形式是以误差函数（error function）：

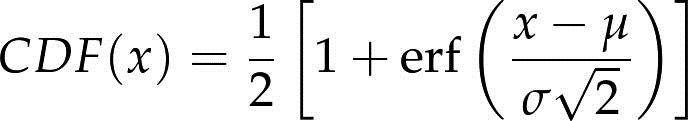
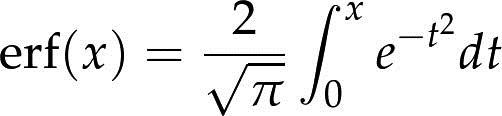
参数μ和σ决定了分布的均值和标准差。其CDF是S形的曲线。

1. 正太分布不能像其他的分布一样，通过转换，判断是否属于正太分布。可用正态概率图（normal probability plot）的方法，它是基于秩变换（rankit）的，所谓秩变换就是对n个服从正态分布的值排序，第k个值分布的均值就称为第k个秩变换。
2. 对数正太分布：一组数值做对数变换后服从正态分布。人的体重服从对数正太分布。

术语：

• 连续分布（continuous distribution） 由连续函数描述的分布。
• 语料库（corpus） 特定语言中用做样本的正文文本。
• 经验分布（empirical distribution） 样本中值的分布。
• 误差函数（error function） 一种特殊的数学函数，因源自误差度量研究而得名。
• 一次频词（hapaxlegomenon） 表示语料库中只出现一次的词。这个单词在本书中迄今出现了两次。
• 间隔时间（interarrival time） 两个事件的时间间隔。
• 模型（model） 一种有效的简化。对于很多复杂的经验分布，连续分布是不错的模型。
• 正态概率图（normal probability plot） 一种统计图形，用于表示样本中排序后的值与其服从正态分布时的期望值之间的关系。
• 秩变换 （rankit） 元素的期望值，该元素位于服从正态分布的已排序列表中。