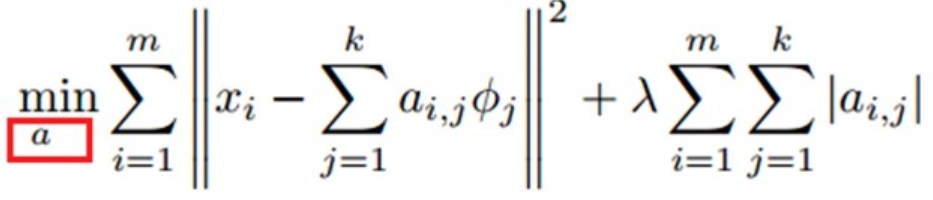目录

• 目录
• 概述
• 代价函数
• 训练求解过程
• 稀疏表示
• 压缩感知
• 参考

概述

稀疏编码（Sparse Coding）：又叫字典学习（Dictionary Learning）：属于一种无监督学习方法，寻求一组超完备的基，更高效的线性表示数据集。

• 字典学习：偏重于学得字典的过程
• 稀疏表示：侧重于对样本进行稀疏表达的过程

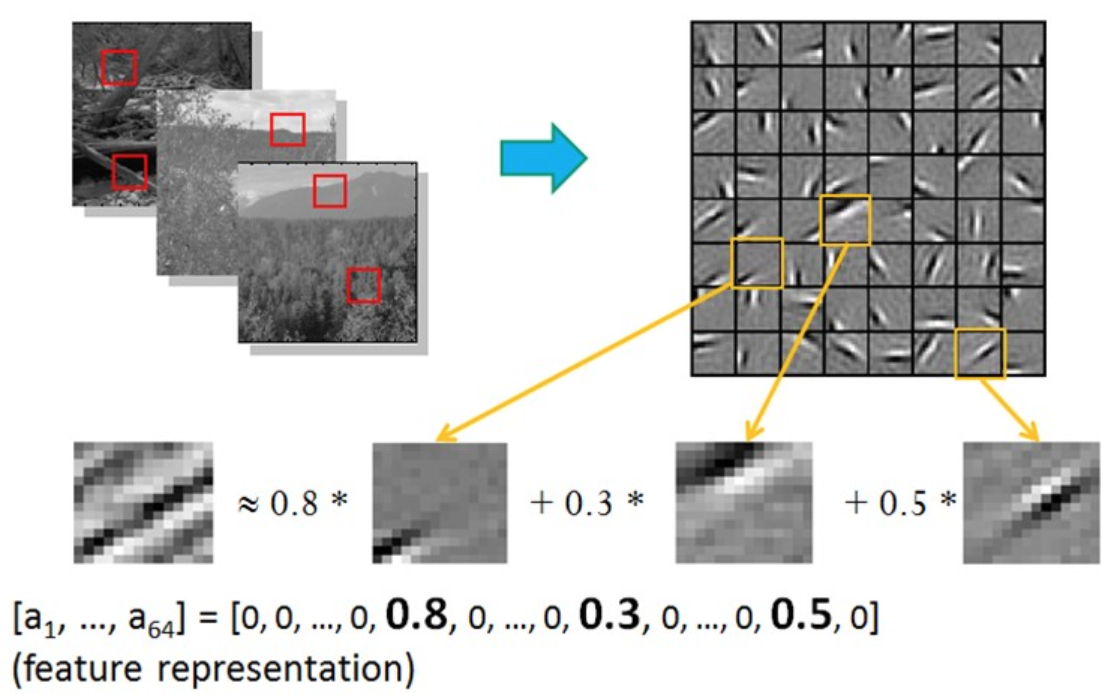
在实际的应用中，稀疏表示的场景很多。比如对于图片，可以学习一组基向量，然后使用这些基向量的线性组合去表示图片。比如下图中，学习了64个基向量，然后用这些基向量去表示一个图片，在表示时其实只有3个是有值的，其他的基向量贡献都为0：

代价函数

• PCA：找一组特征向量，尽可能的表征原始数据，这里的基向量数目小于或等于原始数据的维度。
• PCA vs 稀疏编码：但是在稀疏编码中，是寻找超完备向量，所以其基向量的数目远大于输入向量的维度。
• 代价函数：\(\begin{align} \text{minimize}_{a^{(j)}_i,\mathbf{\phi}_{i}} \sum_{j=1}^{m} \left|\left| \mathbf{x}^{(j)} - \sum_{i=1}^k a^{(j)}_i \mathbf{\phi}_{i}\right|\right|^{2} + \lambda \sum_{i=1}^{k}S(a^{(j)}_i) \end{align}\)
  • m：输入向量的数目
  • X：输入向量
  • \(\phi\)：基向量
  • \(a_i\phi_i\)：向量x的稀疏表示
  • 【第1项】重构项（reconstruction term），迫使稀疏编码算法为输入向量提供一个高拟合度的线性表达式
  • 【第2项】稀疏惩罚项（sparsity penalty term），使输入向量的表达式变得“稀疏”，也就是系数向量a变得稀疏
  • \(\lambda\)：控制这两项式子的相对重要性

训练求解过程

• 基于上面的目标函数进行迭代，求解最小损失时的\(a\)和\(\phi\)。因为有两个参数，所以类似于EM求解。
• 固定\(\phi_k\)，然后调整\(a_k\)，使得上式，即目标函数最小（即解LASSO问题）。【带L1正则化的线性回归问题】
• 固定住\(a_k\)，调整\(\phi_k\)，使得上式，即目标函数最小（即解凸QP问题）。
• 不断迭代，直至收敛。这样就可以得到一组可以良好表示这一系列x的基(\(\phi\))，也就是字典。

稀疏表示

• 表示（coding）：给定一个新的图片x，由上面得到的字典，通过解一个LASSO问题得到稀疏向量a。这个稀疏向量就是这个输入向量x的一个稀疏表达了。
  • 虽然根据样本训练学习得到了一组基向量，但是对于表示新样本的时候，仍然需要优化该样本的系数\(a\)，所以其计算速度很慢。
• 为什么需要稀疏表示：
  • 特征的自动选择：无关的特征其权重都为0
  • 可解释性：只有少数不为0的权重说明此基向量是有作用的
  • 例子：对学习任务有好处。SVM之所以在文本数据上有好的性能，就是由于文本数据在使用字频表示后具有高度的稀疏性，使得大多数问题变得线性可分。

压缩感知

• 现实：根据部分信息来恢复全部信息，数据通讯中将模拟信号转换为数字信号
• 奈奎斯特采样定理：采样频率达到模拟信号最高频率的两倍，则采样后的数字信号就保留了模拟信号的全部信息。数字信号 =》重构 =》原模拟信号

• 接收方基于收到的信号，如何精确重构原信号？压缩感知compressed sensing

• 长度为m的离散信号x
• 采样长度为n的信号：\(y=\Phi x\)
• 如果已知离散信号x和测量矩阵\(\Phi\)，容易得到y值

• 反过来，不易求解。因为这个是欠定方程，无法轻易求出数值解。

• 引入假设：存在线性变换\(y=\Phi x=\Phi \Psi s=As, A=\Phi \Psi, x=\Psi s\)

• 如果能根据y恢复出s，则可通过\(x=\Psi s\)恢复出x的信号

• 只是引入了变换，不解决任何问题？

• 如果s具有稀疏性，那么能很好的解决。稀疏性使得未知因素减少。\(\Psi s\)中的\(\Psi\)称为稀疏基，A的作用类似于字典，能将信号转换为稀疏表示。

• 两个阶段：
  • 感知测量：如何对原始信号进行处理以获得稀疏样本表示。傅里叶变换、小波变换、字典学习、稀疏编码
  • 重构恢复：如何基于稀疏性从少量观测中恢复原信号，这是压缩感知的精髓。
• 压缩感知：
  • 限定等距性：

参考

• 机器学习周志华第11章
• 机器学习——字典学习/稀疏编码学习笔记@知乎
• 稀疏编码Sparse coding
• UFLDL笔记 - Sparse Coding（稀疏编码）
• Sparse Coding @UFLDL