归一化

定义：将数据缩放到特定的区间中，以使得数值之间具有可比较性。

目标：

• 把数变为[0, 1]之间的数值
• 有量纲表达式变为无量纲表达式

为什么需要归一化：

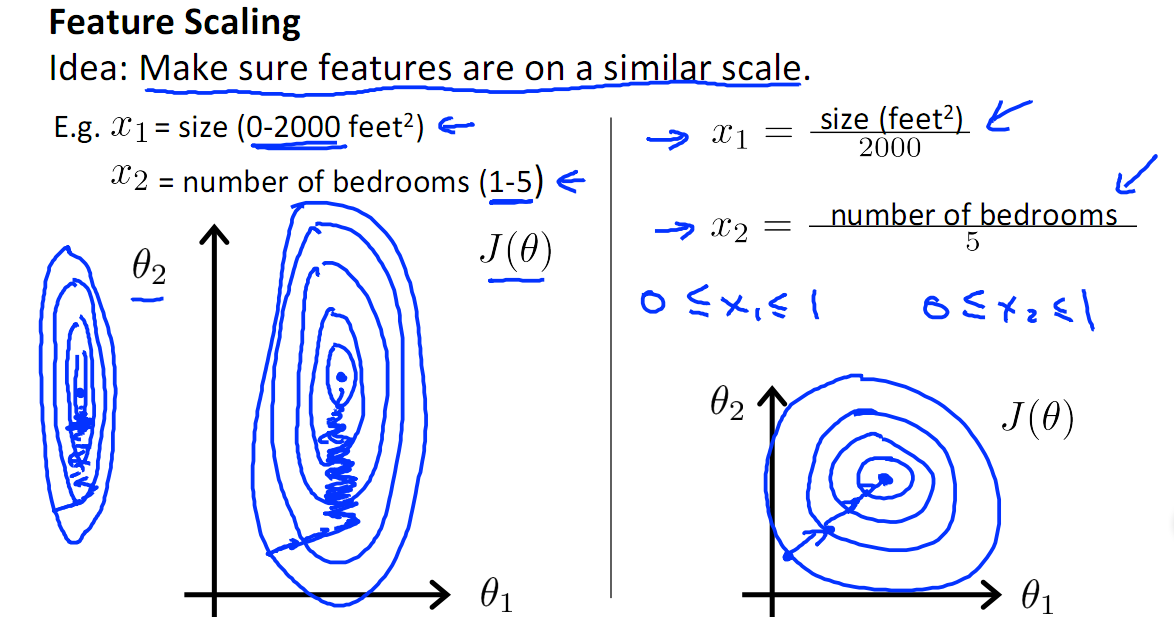
• 提升模型的收敛速度。在梯度下降时，如果不同的特征的值范围差异很大，那么达到全局最小所需的步数就会很多。
• 提升模型的精度。比如在计算相似性（距离等）时，不同数值范围的特征对距离值所产生的影响是不一样的（小的特征值可能不怎么影响），当进行归一化之后，能够使得不同的特征做出的贡献相同。
• 防止梯度爆炸。在神经网络中，梯度爆炸就是由于初始化权值过大，前面层会比后面层变化的更快，就会导致权值越来越大，梯度爆炸的现象就发生了。

哪些模型需要归一化：

• SVM：在特征缩放后，最优解与原来的不等价，所以如果不做缩放，模型参数会被较大或者较小的参数所主导。
• 逻辑回归：在特征缩放后，不会改变最优解，但是如果目标函数过于不均一，收敛会很慢，所以需要归一化。
• 神经网络、SGD：模型效果会强烈的依赖于归一化

哪些模型不需要归一化：

• 特征值在【0，1】之间的不再需要，否则会破坏其原始的稀疏性
• 决策树：效果不受归一化影响
• ICA：不需要归一化
• 最小二乘法OLS：不需要

方法

1. min-max normalization (Rescaling)

公式：\(X_{norm} = \frac{X - X_{min}}{X_{max}-X_{min}}\)

结果：将原始数据经过线性变换，把数值缩放到[0,1]之间，不会改变数据的分布。

2. Mean normalization

公式：\(X_{norm} = \frac{X - X_{mean}}{X_{max}-X_{min}}\)

结果：将原始数据经过线性变换，把数值缩放到[-1,1]之间

3. Standardization (标准化)，z-score标准化，zero-mean normalization

公式：\(X_{norm} = \frac{X - X_{mean}}{\sigma}\)，其中\(\sigma\)是标准差。

结果：转换后的数值，其平均值为0，方差为1，即服从标准正太分布，这个转换不会改变数据的分布。

4. Scaling to unit length

公式：\(X_{norm} = \frac{X}{\|X\|}\)，其中\(\|X\|\)是这个数据向量的欧式长度（Euclidean length）。

结果：转换后的数值在[0,1]之间。

5. log函数转换

公式：\(X_{norm} = \frac{log{X}}{log{X_{max}}}\)

结果：转换后的数值在[0,1]之间。

6. atan函数转换

公式：\(X_{norm} = atan{X}*\frac{2}{\pi}\)

结果：如果X都大于0，则区间映射到[0,1]，小于0的数据映射到[-1,0]之间。

7. quantile normalization

原理：

• 1）记录每个样本（列）中的每个数据的rank（原始rank）；
• 2）每个样本，从小到达排序，计算排序后每个rank的平均值（排序后rank平均值）；
• 3）根据原始rank从排序后rank平均值提取对应的值，取代原来的值，即为归一化之后的值。

结果：使得不同的数据集具有相同的分布，容易比较。（这个方法在microarray数据中使用得很多，原先叫quantile standardization，后来才叫做quantile normalization。wiki给出了一个例子，说的是在不同的样本中，如果将基因的表达量归一化到同一水平。）。下面是不同样本中前后表达量分布的例子：

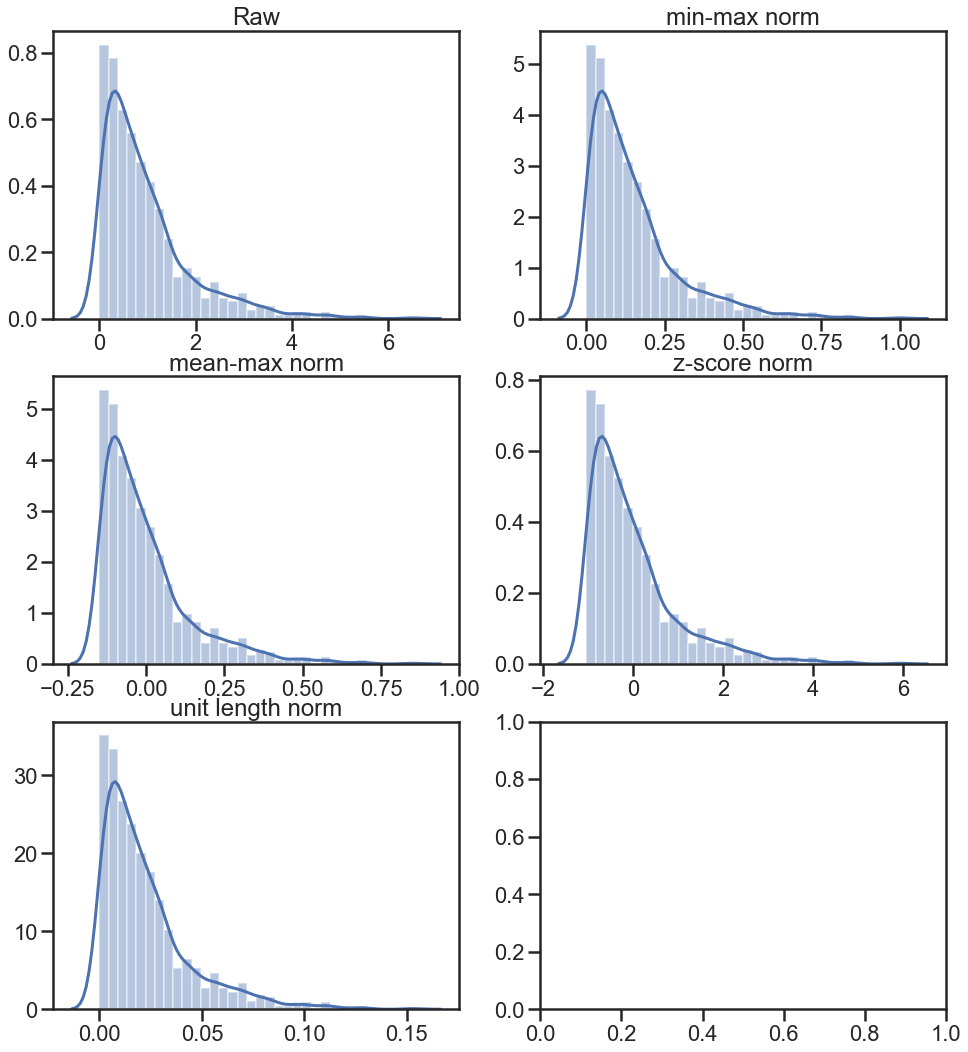
例子比较

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('ticks')

np.random.random(42)
X = np.random.exponential(size=1000)
X_norm_min_max = (X - X.min()) / (X.max() - X.min())
X_norm_mean_max = (X - X.mean()) / (X.max() - X.min())
X_norm_zscore = (X - X.mean()) / X.std()
X_norm_unit = X / np.linalg.norm(X)

fig, ax = plt.subplots(3, 2, figsize=(16,18), sharex=False, sharey=False)
sns.distplot(X, ax=ax[0,0])
ax[0,0].set_title('Raw')
sns.distplot(X_norm_min_max, ax=ax[0,1])
ax[0,1].set_title('min-max norm')
sns.distplot(X_norm_mean_max, ax=ax[1,0])
ax[1,0].set_title('mean-max norm')
sns.distplot(X_norm_zscore, ax=ax[1,1])
ax[1,1].set_title('z-score norm')
sns.distplot(X_norm_unit, ax=ax[2,0])
ax[2,0].set_title('unit length norm')

参考

• Feature_scaling @ wiki
• 数据标准化/归一化normalization
• 标准化和归一化什么区别？
• About Feature Scaling and Normalization
• Preprocessing data@sklearn
• Quantile_normalization @ wiki