[CS229] 04: Linear Regression with Multiple Variables

2018-10-25

04: Linear Regression with Multiple Variables

多特征使得fitting函数变得更复杂，多元线性回归。
多元线性回归的损失函数：
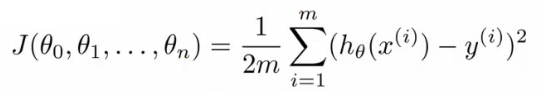
多变量的梯度递减：
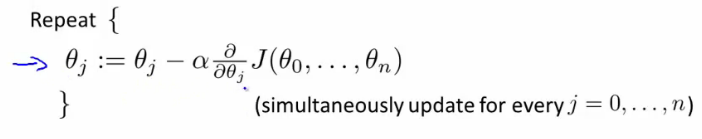
- 规则1：feature scaling。对于不同的feature范围，通过特征缩减到可比较的范围，通常[-1, 1]之间。
- 归一化：1）除以各自特征最大值；2）mean normalization(如下)：
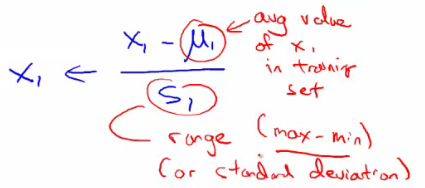
- 规则2：learning rate。选取合适的学习速率，太小则收敛太慢，太大则损失函数不一定会随着迭代次数减小（甚至不收敛）。
- 损失函数曲线：直观判断训练多久时模型会达到收敛
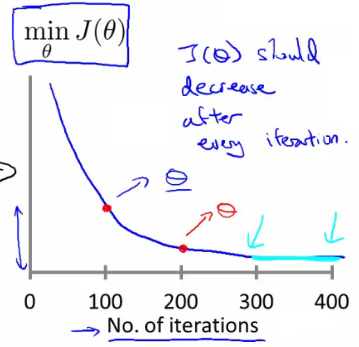
特征和多项式回归：对于非线性问题，也可以尝试用多项式的线性回归，基于已有feature构建额外的特征，比如房间size的三次方或者开根号等，但是要注意与模型是否符合。比如size的三次方作为一个特征，随着size增大到一定值后，其模型输出值是减小的，这显然不符合size越大房价越高。
Normal equation：根据损失函数，求解最小损失岁对应的theta向量的，类似于求导，但是这里采用的是矩阵运算的方式。
- 求解方程式如下：
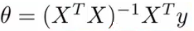
- 这里就直接根据训练集和label值矩阵求解出最小损失对对应的各个参数（权重）。
什么时候用梯度递减，什么时候用normal equation去求解最小损失函数处对应的theta向量？