06: Logistic Regression

1. 逻辑回归：分类，比如email是不是垃圾邮件，肿瘤是不是恶性的。预测y值（label），=1（positive class），=0（negative class）。
2. 分类 vs 逻辑回归（逻辑回归转换为分类）：
   • 分类：值为0或1（是离散的，且只能取这两个值）。
   • 逻辑回归：预测值在[0,1之间]。
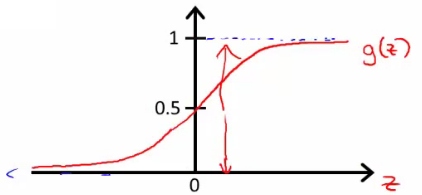
   • 阈值法：用逻辑回归模型，预测值>=0.5，则y=1，预测值<0.5，则y=0.
3. 逻辑回归函数（假设，hypothesis）：
   • 公式：\(\begin{align}h_\theta(x) = \frac{1}{1+\exp(-\theta^\top x)}\end{align}\)
   • 分布：
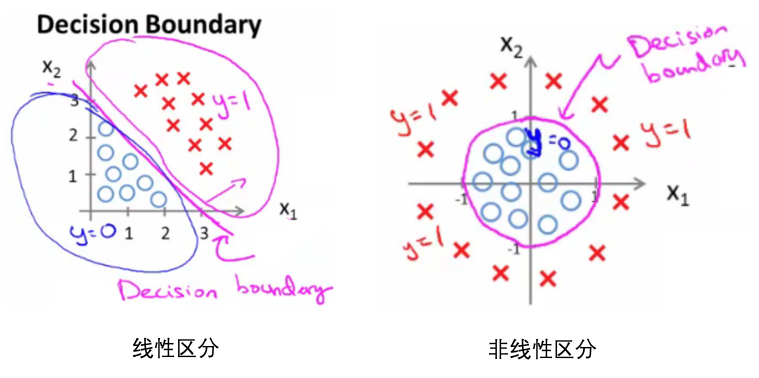
4. 决策边界（decision boundary）：区分概率值（0.5）对应的theta值=0，所以函数=0所对应的线。
   • 线性区分的边界 vs 非线性区分的边界：
5. 损失函数:
   • 问题：
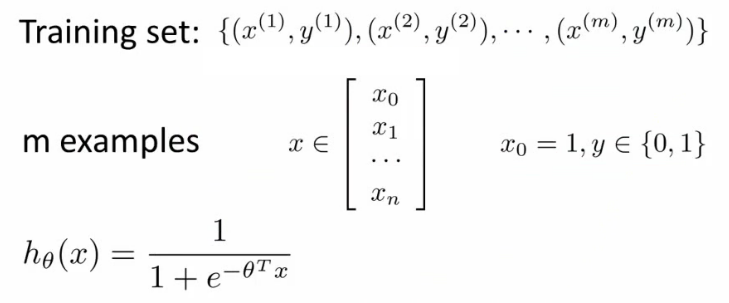
   • 如果延续线性函数的损失函数，则可写成如下，但是当把逻辑函数代入时，这个损失函数是一个非凸优化（non-convex，有很多局部最优，难以找到全局最优）的函数。
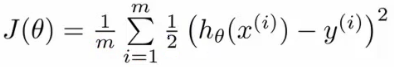
   • 因此，需要使用一个凸函数作为逻辑函数的损失函数：
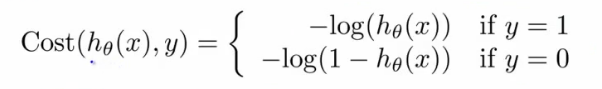
   • 把所有训练样本的误差合在一起：\(\begin{align}J(\theta) = -\left[ \sum_{i=1}^m y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) \right]\end{align}\)
6. 多类别分类：
   • 【one-vs-all】固定一个类别的数据作为正样本，其他所有类别的数据作为负样本，训练模型，预测得到属于某一类别的概率，然后挑选概率最大的即为预测的最终类别。
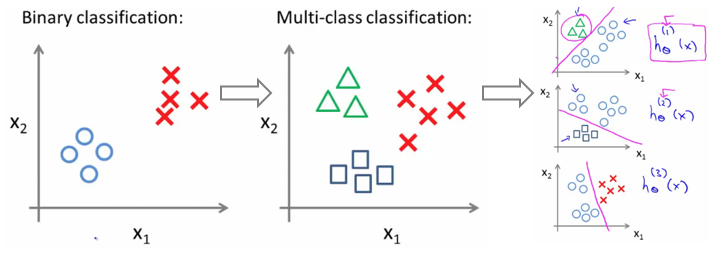
7. 多类别分类：softmax regression多元回归：
   • 参考Softmax Regression @ UFLDL Tutorial和Softmax Regression简介
   • 同义词: Multinomial Logistic, Maximum Entropy Classifier, or just Multi-class Logistic Regression
   • 这里提供了一个关于二元和多元逻辑回归的比较（包括其提到的例子可以看一下）：
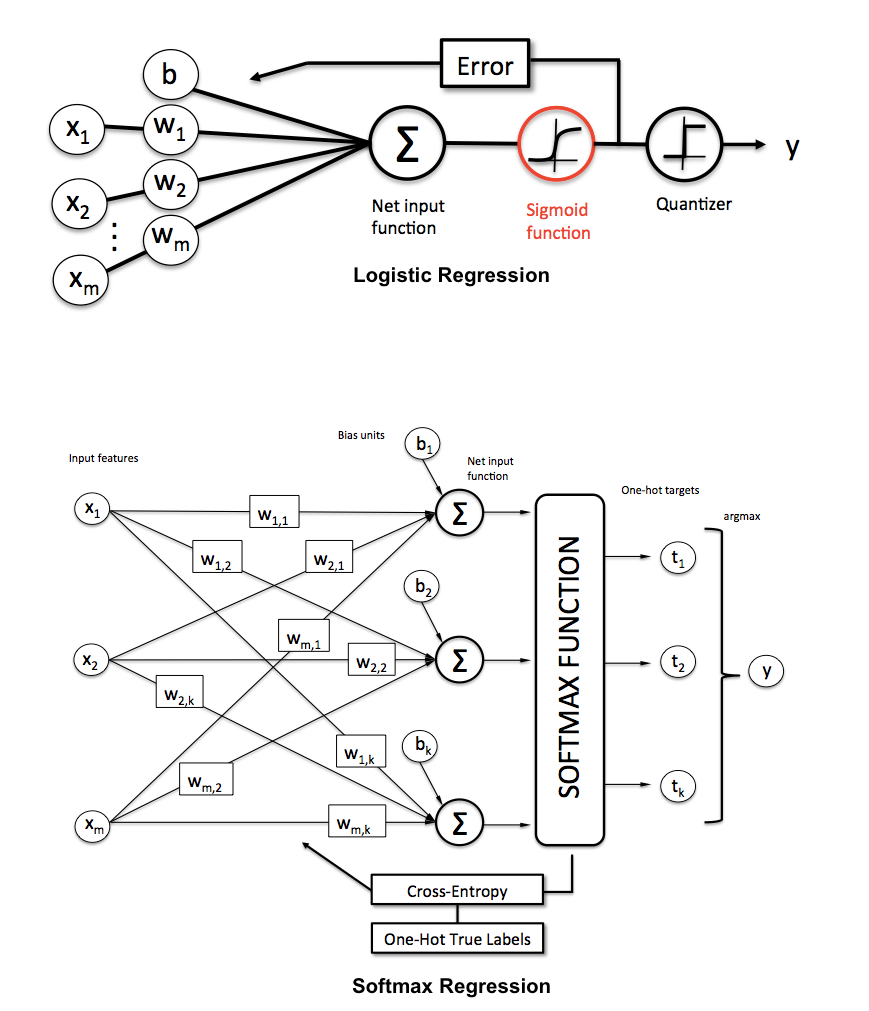
   • 因为是多类别，所以（模型）输出是每个类别的概率（对于某个样本和参数\(\theta\)，输出属于每个类别的概率）：\(\begin{align} h_\theta(x) = \begin{bmatrix} P(y = 1 | x; \theta) \\ P(y = 2 | x; \theta) \\ \vdots \\ P(y = K | x; \theta) \end{bmatrix} = \frac{1}{ \sum_{j=1}^{K}{\exp(\theta^{(j)\top} x) }} \begin{bmatrix} \exp(\theta^{(1)\top} x ) \\ \exp(\theta^{(2)\top} x ) \\ \vdots \\ \exp(\theta^{(K)\top} x ) \\ \end{bmatrix} \end{align}\)
   • 损失函数：和逻辑回归类似，只是这里是对于K个类别的加和：\(\begin{align} J(\theta) &= - \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\ &= - \left[ \sum_{i=1}^{m} \sum_{k=0}^{1} 1\left\{y^{(i)} = k\right\} \log P(y^{(i)} = k | x^{(i)} ; \theta) \right] \end{align} \\\) 这里1{.}叫做指示函数（indicator function），如果括号内容为真，则值为1，为假则值为0.
   • 类别概率：\(\begin{align}P(y^{(i)} = k \| x^{(i)} ; \theta) = \frac{\exp(\theta^{(k)\top} x^{(i)})}{\sum_{j=1}^K \exp(\theta^{(j)\top} x^{(i)}) }\end{align}\)，某个样本所有类别的概率和为1.
   • 这里的参数优化使用梯度下降法，梯度更新如下：\(\begin{align} \nabla_{\theta^{(k)}} J(\theta) = - \sum_{i=1}^{m}{ \left[ x^{(i)} \left( 1\{ y^{(i)} = k\} - P(y^{(i)} = k | x^{(i)}; \theta) \right) \right] } \end{align}\)