14: Dimensionality Reduction

1. 降维：非监督学习算法，用更简化的表示方法表征收集的数据。
2. 为啥降维 -》压缩：
   • 高维的数据用低维表征
   • 加速算法，节省存储空间
   • 例子：1）二维数据点用一维表示，x1和x2只是两个不同的单位（冗余）；2）三维数据点用二维表示，所有的点在一个平面上，此平面用二维即可定义：
   • 实际中可以做到：1000维 =》100维
3. 为啥降维 -》可视化：
   • 高维数据难以可视化
   • 降维可以将数据以人可以理解的方式展现出来
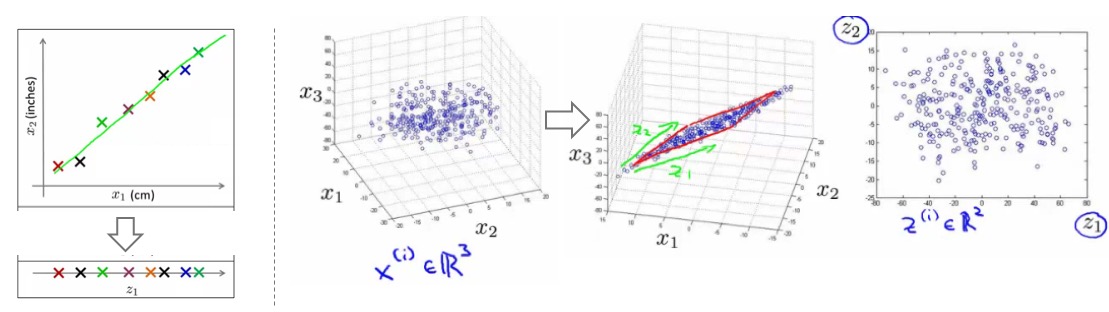
   • 比如一个表格，使用了50多个特征描述不同的国家，从这里我们能得到什么信息？
   • 通常很难理解具体的降维之后的特征所表示的意思
4. 主成分分析（PCA）：
   • 例子：2D数据降至1D，所以需要找一个一维的向量，使得所有点在这个向量的投射误差最小：
   • 投映误差（projection error）：点到向量的垂直距离（orthogonal distance），下图中的蓝色线条
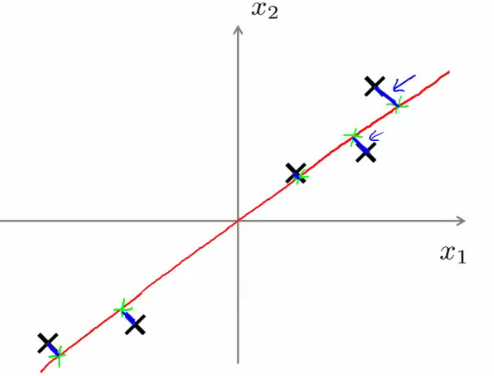
   • 在做PCA之前，一定要对数据进行预处理：平均值归一化（mean normalization）和特征缩放（feature scaling）
   • 广泛定义：
   • nD -> kD，在将数据从n维降至k维时，需要找k个向量，使得所有数据投射到这些向量时，投映误差最小。找的向量需要能最大程度的保留原来的信息，冗余的信息可以只保留部分信息，所以需要找的向量应该是波动最大（variance最大）的方向，这样也能保证投射误差最小。所以选取的k个方向，也是差异最大的k个方向。3D -> 2D：找两个向量。
   • 特征向量：数据变化的方向向量。一个k维的数据，就有k个变化的方向，且不同的方向变化大小是不一样的。
5. PCA vs 线性回归：
   • PCA和线性回归很像，但PCA不是线性回归，其差别很大
   • 线性回归：拟合直线，使得y方向的差值（vertical distance，预测的误差）最小，因为线性回归是有y值的；
   • PCA：没有y值，只有特征值（且这些特征值都是同等对待的）。所以是找向量，误差的计算用的是垂直距离（orthogonal distance）。
6. PCA算法：
   • 【预处理：均值归一化】：对于每个特征，进行均值归一化，x -> x-mean(x)。每个特征的均值归一化到0.
   • 【预处理：特征缩放】：当特征的区间差异很大时，需要进行缩放使得数值在可比较的区间里。1）Biggest - smallest；2）Standard deviation（标准差缩放更常见）
   • 计算2个向量：1）新的平面向量u；2）新的特征向量z。
   • 比如2D -> 1D，要计算向量u和新的特征向量：
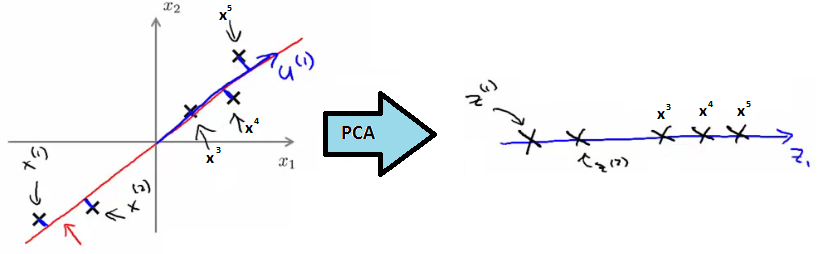
7. 算法描述（这里有计算的步骤描述，可参考）：
   • 1）数据预处理：中心化，归一化。（对于图像、音频、文本等数据，通常不用做variance normalization归一化，比如特征乘以一个数，PCA计算的特征向量是一样的。）
   • 2）根据样本计算协方差矩阵
   • 3）利用特征值/奇异值分解，求特征值和特征向量
   • 4）用特征向量构造投影矩阵
   • 5）利用投影矩阵和样本数据，计算降维的数据
8. 如何选取k：
   • 通常会定义一个比值=平均投影误差/数据本身总方差：
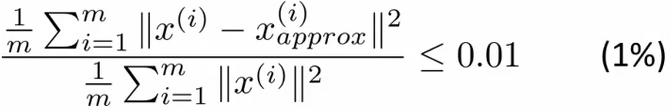
   • 这个数值越小越好，越小说明丢失的信息越少，保留的信息越多。
   • 实际操作：从k=1开始尝试，看哪个能满足上面的比值<=0.01，最小的能够满足这个比例的k值是我们想要的：
   • 通过投影矩阵还原原始数据，我们只能用一个近似的原则。因为保留的k维是原始数据差异最大的，其他的维度差异近似为0，所以可以通过补充0的方式，来（近似）还原原始的数据：\(\begin{align} \hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}\)
9. PCA可加速监督式学习算法：
   • 比如对于具有超高维特征的数据，可先用PCA进行降维，使用降维后的数据和原始的标签进行模型的训练，再去对于新的数据进行预测。
   • 新数据：怎么预测？特征数目或者叫维度不一样！！！在上面的PCA中计算了参数投影矩阵。
10. PCA应用：
    • 压缩：减少存储，加速算法。保留多少的variance来确定k值。
    • 可视化：通常降至2-3维
    • 错误使用PCA避免过拟合：以为具有更少的特征就能避免过拟合，实则不然。应该使用正则化防止过拟合。
    • 至少95%-99%的信息是需要保留的。
    • 在使用PCA之前，先尝试不使用时能否达到预期的效果。
11. 白化（whitening）：目的是降低特征之间的相关性，特征的方差归一化
    • 训练图片，相邻的像素是高度冗余的（特征具有强相关性）
    • 通常学习算法希望的特征是：1）不相关的；2）具有相同的variance（彼此方差接近）。
12. PCA-whitening：
    • 是基于PCA的，包括两个步骤
    • 1）使用PCA进行降维，消除特征之间的相关性：\(\textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}\)
    • 2）方差归一化：\(\begin{align} x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \end{align}\)
    • 这样就得到了白化的PCA，依然选取前k个作为主成分。
13. ZCA-Whitening：
    • 另外的一种白化方式，同样能够实现减少相关特征，方差归一化的目的。
    • UFLDL笔记 - PCA and Whitening 一文较为详细的描述了PCA白化和ZCA变化的区别，可以参考一下。
    • PCA白化是将原始数据投影到主成分轴上（消除特征相关性），然后对特征轴上的数据进行归一化（方差全缩放为1）。这些操作是在主成分空间完成的，为了使得白化的数据尽可能接近原始数据，所以可以把白化的数据转换回原始数据，这就是ZCA白化所做的事情。
    • ZCA白化相当于将经过PCA白化后的数据重新变换回原来的空间。