16: Recommender Systems
- 推荐系统:尝试鉴定重要而相关的特征
- 重要的机器学习应用,在工业界其很大的作用
- 其思想很重要,说明了通过模型学习能知道哪些特征的重要性
- 例子:预测对电影的评分
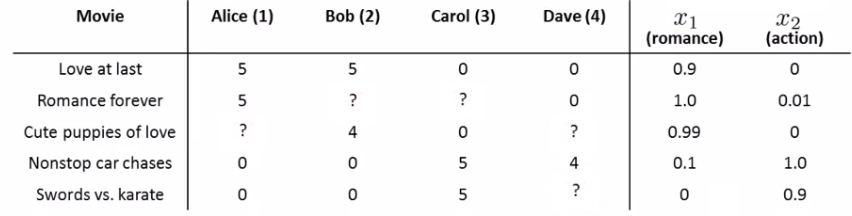
- 不同用户(用户数目:\(n_u\))对不同电影(电影数目\(\begin{align} n_m \end{align}\))的评价(\(\begin{align} y^{ij} \end{align}\)),评价与否:\(r(i,j)\)评价即为1.
- 问题描述:对于给定的\(r(i,j)\)和\(\begin{align} y^{ij} \end{align}\),预测表格中的缺失值(用户对电影的评价值)。
- 不同用户(用户数目:\(n_u\))对不同电影(电影数目\(\begin{align} n_m \end{align}\))的评价(\(\begin{align} y^{ij} \end{align}\)),评价与否:\(r(i,j)\)评价即为1.
- 基于(电影)内容的推荐(content-based approach):
- 如何学习参数向量(\(\theta^j\)):
- 协同过滤(collaborative filtering):
- 特性:自行学习什么样的特征是需要学习的
- 基于内容的假设:电影的特征标签是已知的
- 这里的协同过滤:对于电影的任何特征标签是不知道的
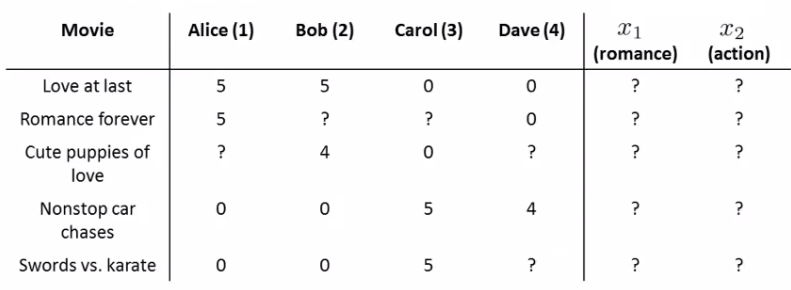
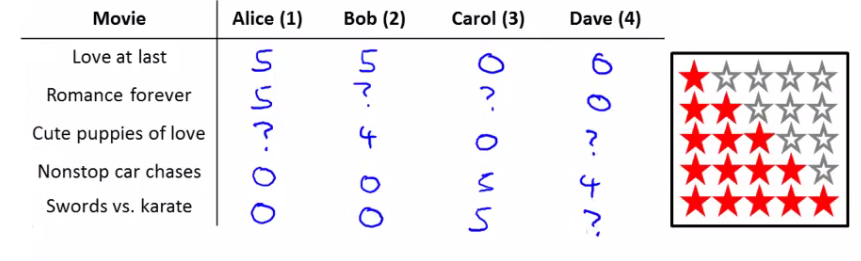
- 协同过滤的假设:调查了用户,获得了用户的喜好 。比如几位用户的喜好特征向量([爱情片,动作片,其他])如下:
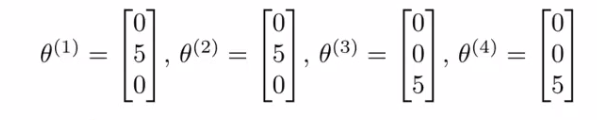
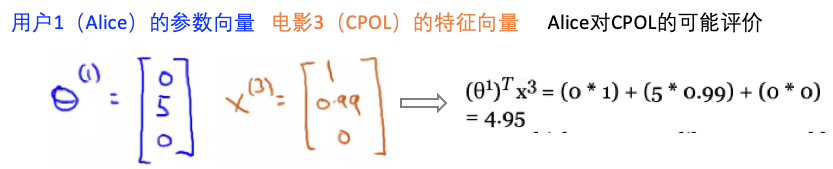
- 【直观】从这里可知,用户1、2喜好爱情片,同时从表中看到用户1、2也喜欢第一个电影(评价很高5颗星),所以推测第一个电影”Love at Last“是一个爱情片。
- 【目标】找到电影1的特征向量\(x^1\),使得\((\theta^1)^T x^1=5\), \((\theta^2)^T x^1=5\), \((\theta^3)^T x^1=0\), \((\theta^4)^T x^1=0\).
- 同理,可以求得其他电影对应的特征向量
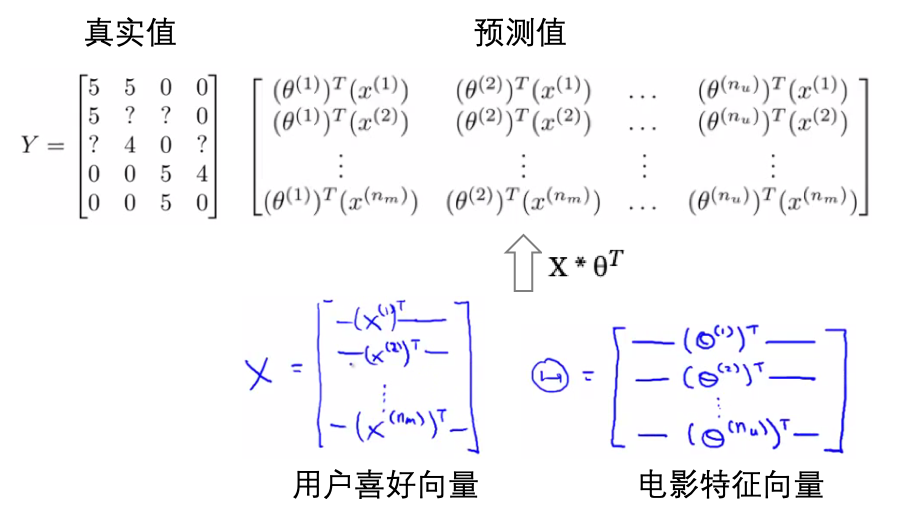
- 协同过滤公式化:
- 给定用户的喜好(参数)向量,求解每个电影对应的特征向量,最小化下面的损失函数(这里的损失函数和上面的基于内容的是一样的,都是为了最小化预测偏差,只是这里我们知道的是用户的参数偏好向量,要求得电影的特征向量):
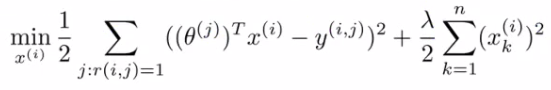
- 给定用户的喜好(参数)向量,求解每个电影对应的特征向量,最小化下面的损失函数(这里的损失函数和上面的基于内容的是一样的,都是为了最小化预测偏差,只是这里我们知道的是用户的参数偏好向量,要求得电影的特征向量):
- 结合起来:
- 基于内容:已知电影的特征向量,学习用户的喜好
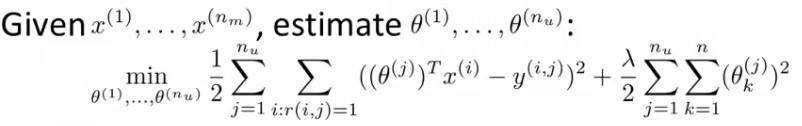
- 协同过滤:已知用户的喜好,学习电影的特征向量
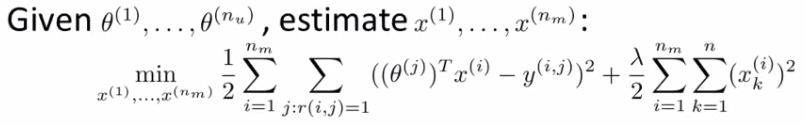
- 实际操作:1)随机初始化用户的喜好向量\(\theta\),2)使用协同过滤的方式学习电影的特征向量 \(X\),3)使用基于内容的方式提高\(\theta\),4)然后再提高\(X\),如此反复。
- 为啥叫协同过滤:用户参与进来,一起帮助学习算法更好的学习特征
- 基于内容:已知电影的特征向量,学习用户的喜好
- 协同过滤的一步化:
- 上面的实际操作是\(\theta\)和\(X\)分别交替学习优化的,有没有一步化的方式更高效的可以同时学习的方式?
- 如下,同时优化\(\theta\)和\(X\):
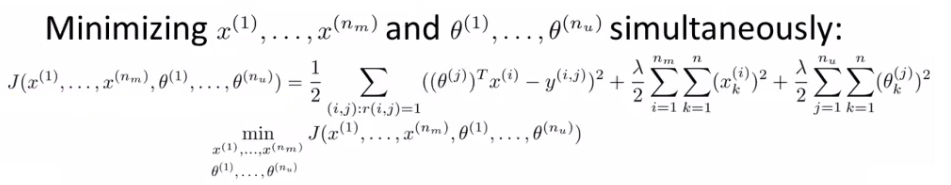
- 协同过滤的一步化的算法结构:
- 1)用较小的值随机初始化用户的喜好向量\(\theta\)和电影的特征向量\(X\)(类似于神经网络)
- 2)使用梯度下降法优化上面的损失函数(同时优化\(\theta\)和\(X\))
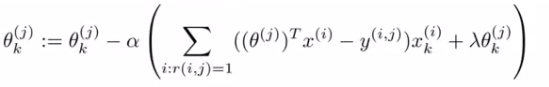
- 3)当达到最小损失时,就求得了用户的喜好向量和电影的特征向量。
- 4)对于某个用户对某个某个电影的评价,就可以通过公式求得:评价=\({(\theta^j)}^T X^i\)
- 以向量的形式求解偏好向量和特征向量:
- 如何推荐电影:
- 通过上面的协同过滤算法,我们可以得到用户的偏好向量和电影的特征向量,但是还没有实现向用户推荐电影,如何推荐?
- 计算电影的相似性:现在每个电影的特征是知道的,对于某用户评价高的电影,计算其他电影与这个电影的相似性,相似性高的就推荐。
- 两个电影的特征向量:\(x^i\), \(x^j\), 最小化:\(x^i-x^j\),即两个电影之间的距离
- 均值归一化(为什么需要):

- 这里用户5Eve没有做任何的评价
- 假如n=2,我们要学习用户5Eve的喜好向量\(\theta5\)。下面是其损失函数,这里没有做任何评价,所以r(i,j)=1的是没有的,第一项可以忽略。优化最后的正则项,这里假设的是两个电影,所以损失是:\(\lambda/2[{\theta^5_1}^2 + {\theta^5_2}^2]\),要使得这个最小,那么\(\theta5=[0,0]\)

- 【问题】这样一来,对于任何电影,所有的预测值都是0(不喜欢任何电影)。
- 均值归一化:
- 首先计算每个电影的平均评价,然后对于原始的评价进行均值归一化
- 预测评价=\({(\theta^j)}^T X^ + u_i\)
- 同样的求得\(\theta5=[0,0]\),所以对任何电影,其评价得分(=0+\(u_i\))就是该电影的平均评价得分(这个是基于其他人对这个电影的评价)。
If you link this blog, please refer to this page, thanks!
Post link:https://tsinghua-gongjing.github.io/posts/CS229-16-Recommender-Systems.html
Previous:
Outliner Detection
Next:
Stanford deep learning
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me