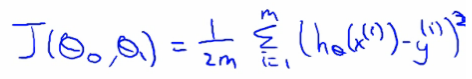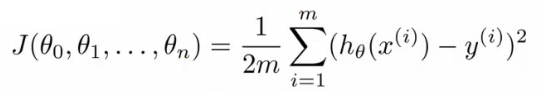课程信息
机器学习入门,Coursera的课程内容和CS229的内容相似,但是后者的难度更大,有更多对于公式的推导,可以先看Coursera再补充看CS229的。
- Coursera video: https://www.coursera.org/learn/machine-learning
- Coursera video slides and quiz on Github (fork from atinesh-s): https://github.com/Tsinghua-gongjing/Coursera-Machine-Learning-Stanford
-
Webpage notes: http://www.holehouse.org/mlclass/
- Stanford course material: http://cs229.stanford.edu/syllabus.html
-
Stanford video: https://see.stanford.edu/course/cs229
- CS229 cheatsheet:English & Chinese & @Stanford
课程笔记
- 注意:
很多介绍的内容都很详细,这里只记录一些自己觉得容易忘记或者难以理解的点。
01 and 02: Introduction, Regression Analysis and Gradient Descent
- definition: a computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E . — Tom Mitchell (1998)
- supervised learning:
- supervised learning: “right answers” given
- regression: predict continuous valued output (e.g., house price)
- classification: predict discrete valued output (e.g., cancer type)
- unsupervised learning:
- unlabelled data, using various clustering methods to structure it
- examples: google news, gene expressions, organise computer clusters, social network analysis, astronomical data analysis
- cocktail party problem: overlapped voice, how to separate?
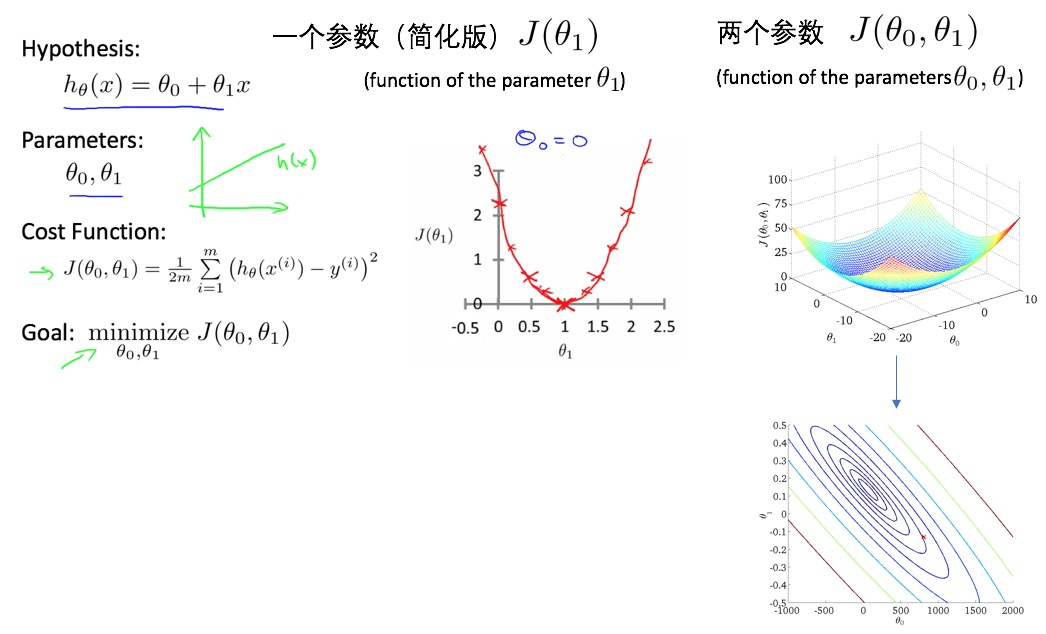
- linear regression one variable (univariate):
- parameter estimation: gradient decent algorithm
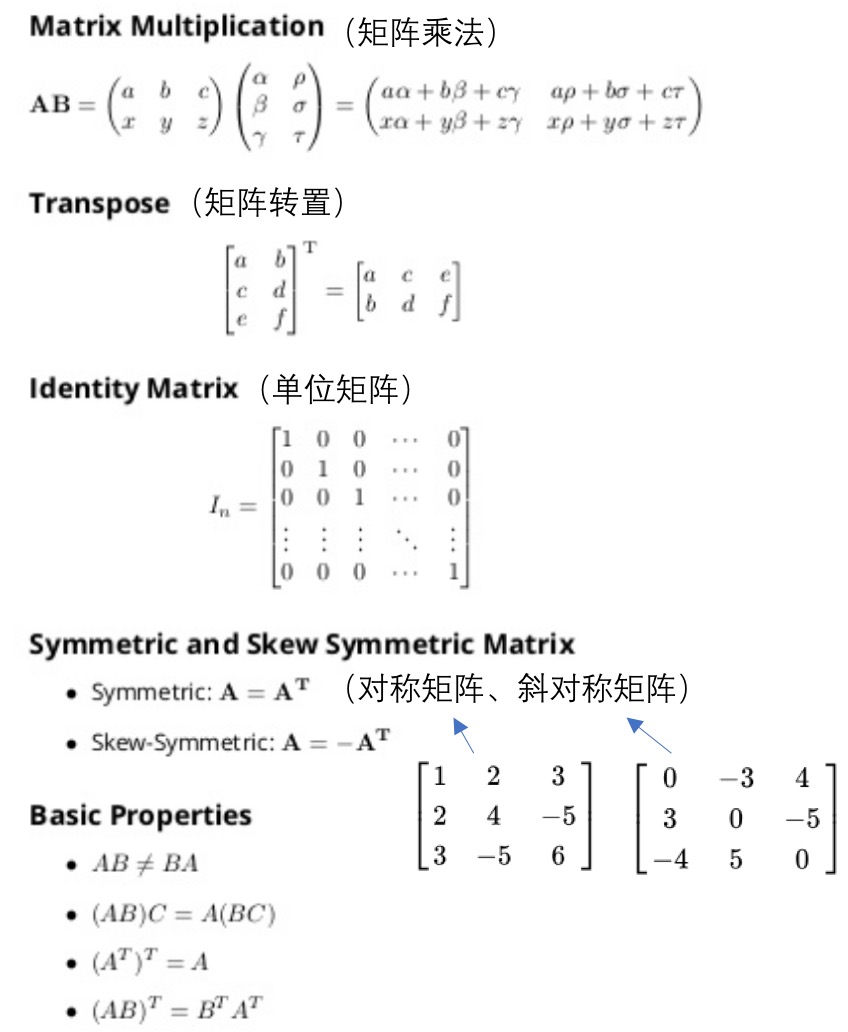
03: Linear Algebra - review
- 概念:
- matrix: rectangular array of numbers: rows x columns
- element: i -> ith row, j -> jth column
- vector: a nx1 matrix
- 操作:
04: Linear Regression with Multiple Variables
- 多特征使得fitting函数变得更复杂,多元线性回归。
- 多元线性回归的损失函数:
- 多变量的梯度递减:
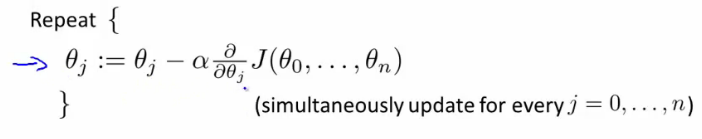
- 规则1:feature scaling。对于不同的feature范围,通过特征缩减到可比较的范围,通常[-1, 1]之间。
- 归一化:1)除以各自特征最大值;2)mean normalization(如下):
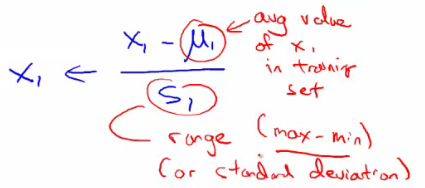
- 规则2:learning rate。选取合适的学习速率,太小则收敛太慢,太大则损失函数不一定会随着迭代次数减小(甚至不收敛)。
- 损失函数曲线:直观判断训练多久时模型会达到收敛
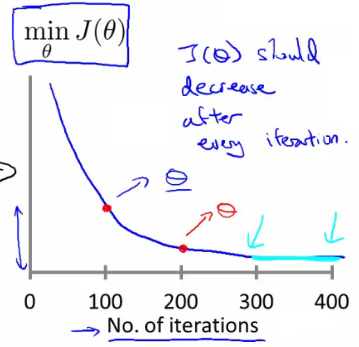
- 特征和多项式回归:对于非线性问题,也可以尝试用多项式的线性回归,基于已有feature构建额外的特征,比如房间size的三次方或者开根号等,但是要注意与模型是否符合。比如size的三次方作为一个特征,随着size增大到一定值后,其模型输出值是减小的,这显然不符合size越大房价越高。
- Normal equation:根据损失函数,求解最小损失岁对应的theta向量的,类似于求导,但是这里采用的是矩阵运算的方式。
- 求解方程式如下:
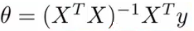
- 这里就直接根据训练集和label值矩阵求解出最小损失对对应的各个参数(权重)。
- 什么时候用梯度递减,什么时候用normal equation去求解最小损失函数处对应的theta向量?
05: Octave[incomplete]
06: Logistic Regression
- 逻辑回归:分类,比如email是不是垃圾邮件,肿瘤是不是恶性的。预测y值(label),=1(positive class),=0(negative class)。
- 分类 vs 逻辑回归(逻辑回归转换为分类):
- 分类:值为0或1(是离散的,且只能取这两个值)。
- 逻辑回归:预测值在[0,1之间]。
- 阈值法:用逻辑回归模型,预测值>=0.5,则y=1,预测值<0.5,则y=0.
- 逻辑回归函数(假设,hypothesis):
- 公式:
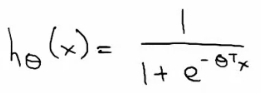
- 分布:
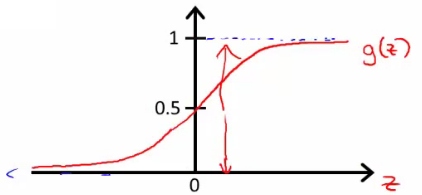
- 公式:
- 决策边界(decision boundary):区分概率值(0.5)对应的theta值=0,所以函数=0所对应的线。
- 线性区分的边界:
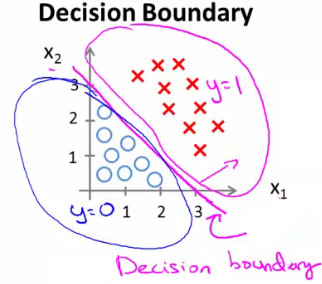
- 非线性区分的边界:
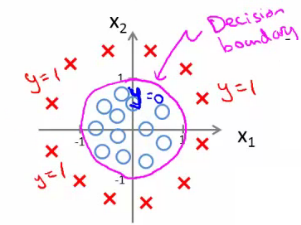
- 线性区分的边界:
- 损失函数:
- 问题:
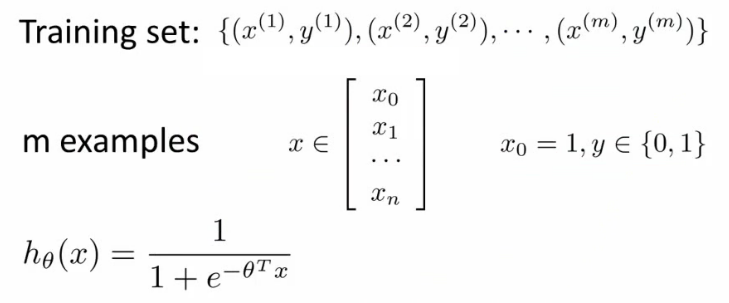
- 如果延续线性函数的损失函数,则可写成如下,但是当把逻辑函数代入时,这个损失函数是一个非凸优化(non-convex,有很多局部最优,难以找到全局最优)的函数。
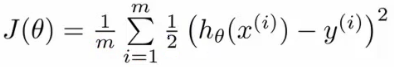
- 因此,需要使用一个凸函数作为逻辑函数的损失函数:
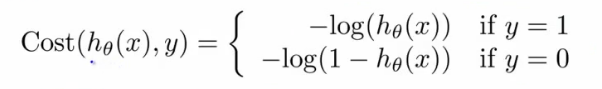
07: Regularization
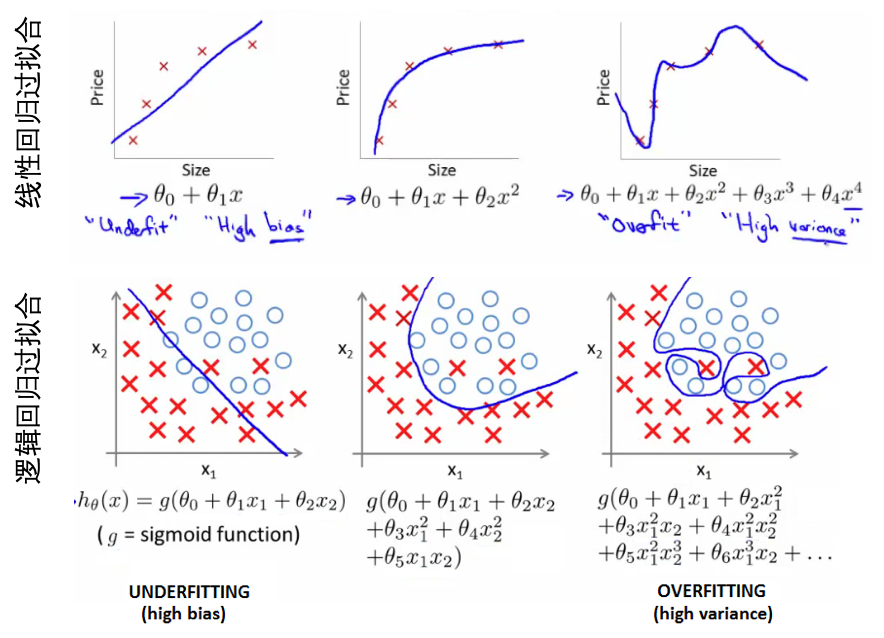
- 过拟合的问题:
- 如何解决过拟合:
- 如何鉴定是否过拟合?泛化能力很差,对新样本的预测效果很糟糕。
- 低维时可以画出来,看拟合的好坏?高维时不能很好的展示。
- 特征太多,数据太少容易过拟合。
- 方案【1】减少特征数目。1)手动挑选特征;2)算法模型挑选;3)挑选特征会带来信息丢失
- 方案【2】正则化。1)保留所有特征,但是减小权重函数的量级;2)当有很多特征时,每一个特征对于预测都贡献一点点。
- 正则化:
- 参数值较小时模型越简单
- 简单的模型更不容易过拟合
- 加入正则项,减小每个参数的值
- 加入正则项后的损失函数:
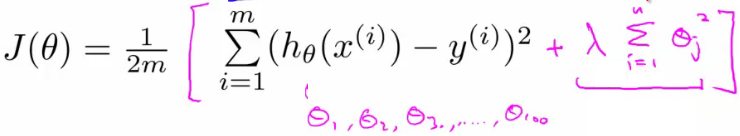
- λ正则化参数:平衡模型对于训练数据的拟合程度,和所有参数趋于小(模型趋向于简单)
08: Neural Networks - Representation
- 非线性问题:线性不可分,增加各种特征使得可分。比如根据图片检测汽车(计算机视觉)。当特征空间很大时,逻辑回归不再适用,而神经网络则是一个更好的非线性模型。
- 神经网络:想要模拟大脑(不同的皮层区具有不同的功能,如味觉、听觉、触觉等),上世纪80-90年代很流行,90年达后期开始没落,现在又很流行,解决很多实际的问题。
- 神经网络:
- cell body, input wires (dendrities, 树突), output wire (axon,轴突)
- 逻辑单元:最简单的神经元。一个输入层,一个激活函数,一个输出层。
- 神经网络:激活函数,权重矩阵:
- 输入层,输出层,隐藏层
- ai(j) - activation of unit i in layer j
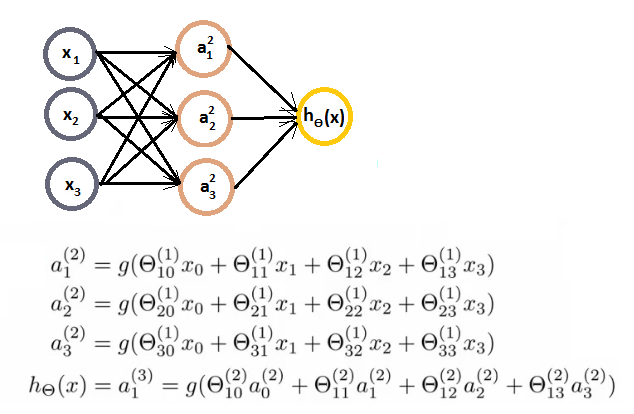
- 前向传播:向量化实现,使用向量表示每一层次的输出。
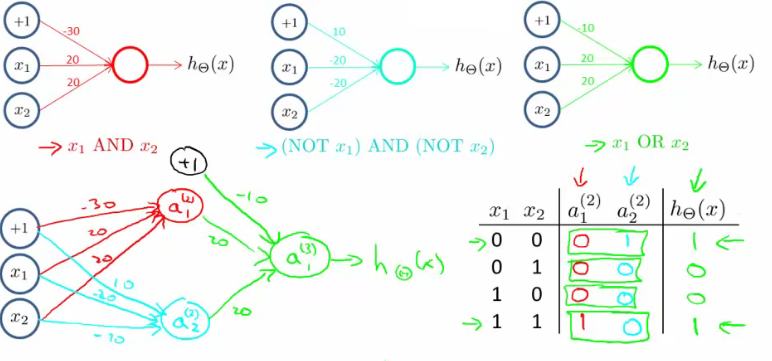
- 使用神经网络实现逻辑符号(逻辑与、逻辑或,逻辑和):
- 实现的是逻辑,而非线性问题,所以神经网络能很好的用于非线性问题上。
- 下面的是实现 XNOR (NOT XOR):
- 多分类问题:one-vs-all
09: Neural Networks - Learning
- 神经网络分类问题:
- 二分类:输出为0或1
- 多分类:比如有k个类别,则输出一个向量(长度为k,独热编码表示)
- 损失函数:类比逻辑回归的损失函数
- 逻辑回归的损失函数(对数损失+权重参数的正则项):
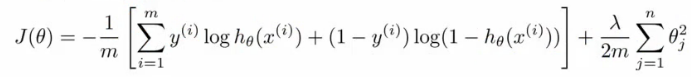
- 神经网络的损失函数:
- 注意1:输出有k个节点,所以需要对所有的节点进行计算
- 注意2:第一部分,所有节点的平均逻辑对数损失
- 注意3:第二部分,正则和(又称为weight decay),只不过是所有参数的
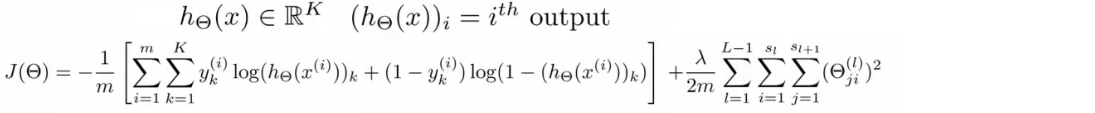
- 前向传播(forward propagation):
- 训练样本、结果已知
- 每一层的权重可以用theta向量表示,这也是需要确定优化的参数
- 每一层的激活函数已知
- 就可以根据以上的数据和参数一层一层的计算每个节点的值,并与已知的值进行比较,构建损失函数
- 反向传播(back propagation):
- 每一层的每个节点都会计算出一个值,但是这个值与真实值是有差异的,因此可以计算每个节点的错误。
- 但是每个节点的真实值我们是不知道的,只知道最后的y值(输出值),因此需要从最后的输出值开始计算。
- 这个文章: 一文弄懂神经网络中的反向传播法——BackPropagation通过一个简单的3层网络的计算,演示了反向传播的过程,可以参考一下:
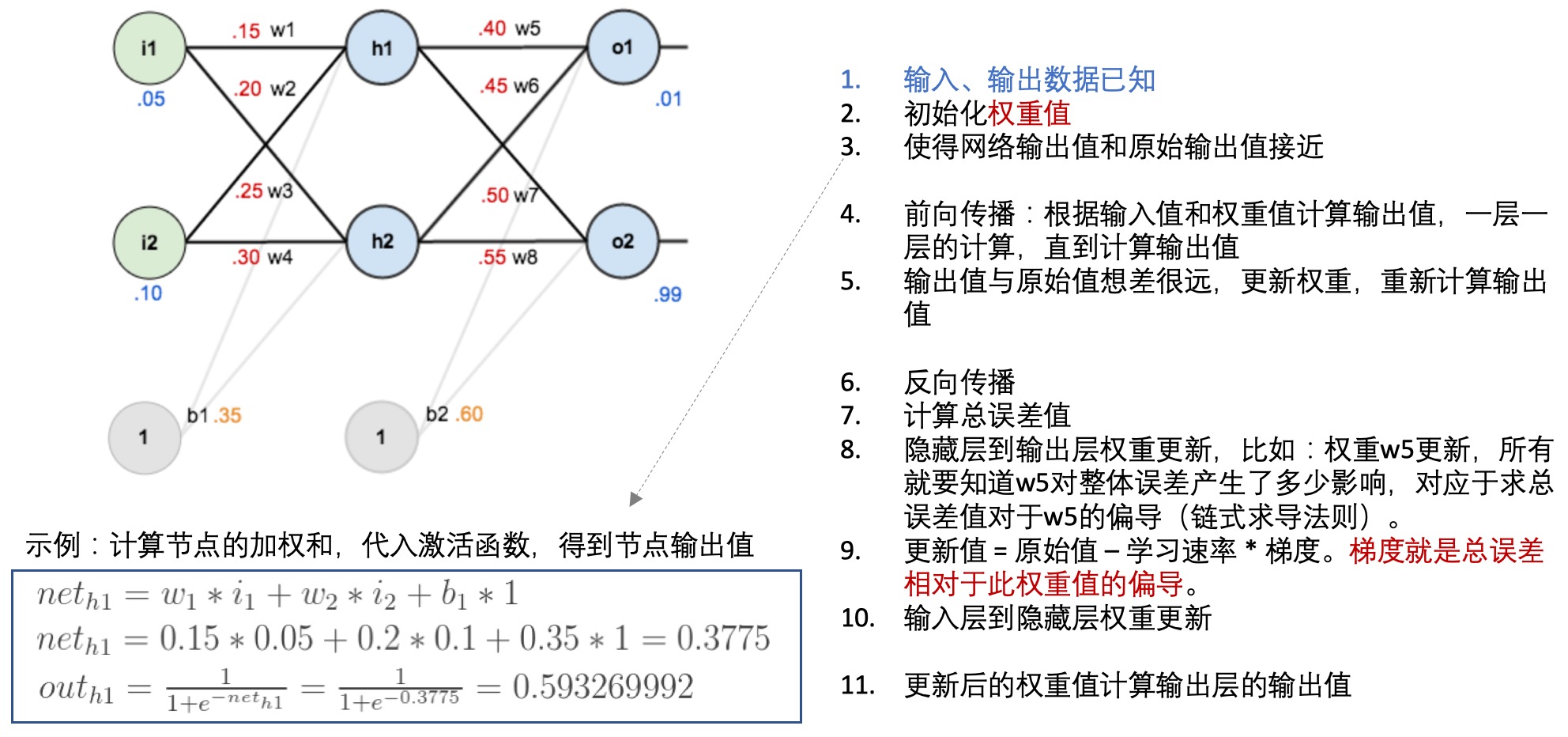
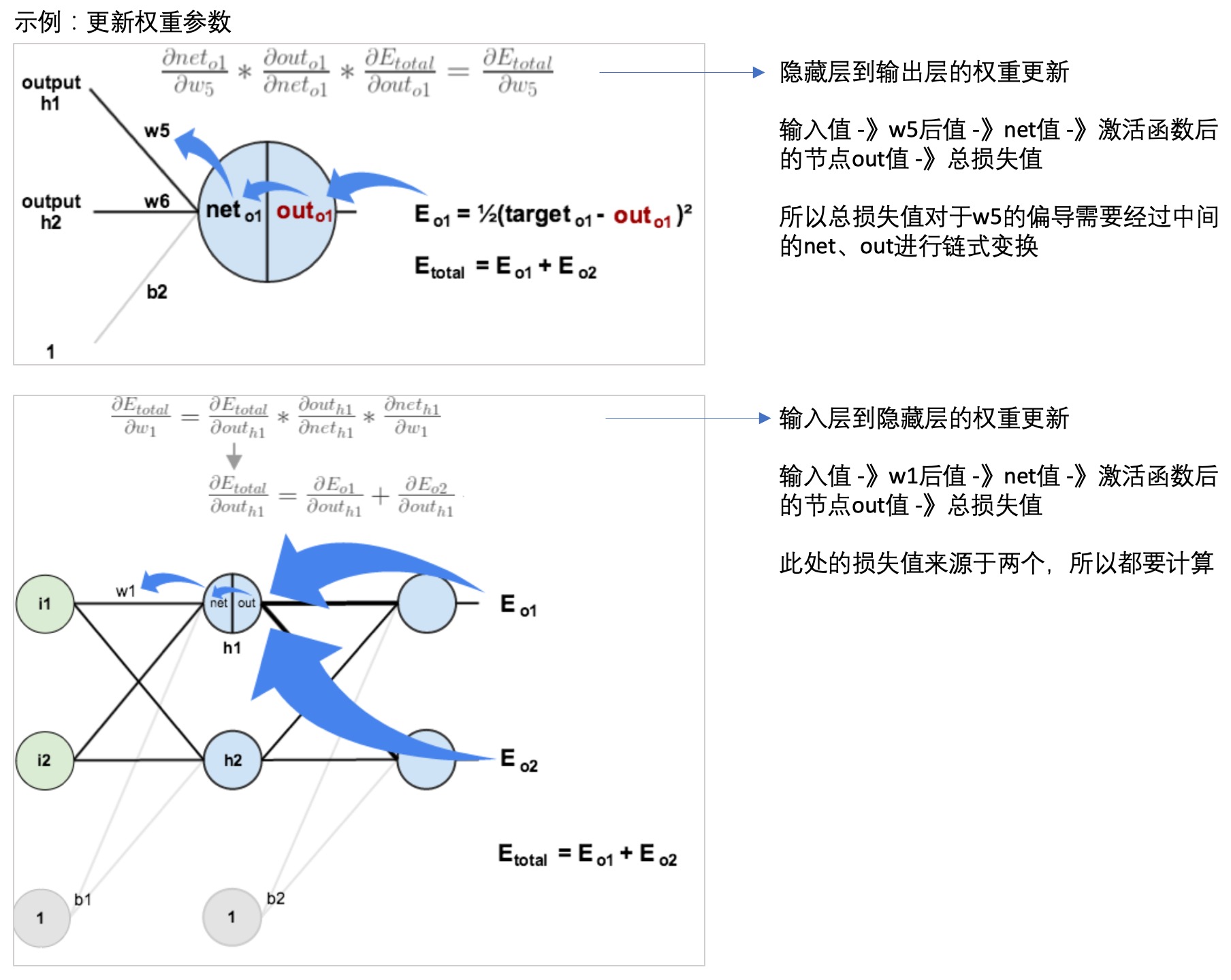
- 神经网络学习:
10: Advice for applying machine learning techniques
- 算法debug:
- 更多的训练样本 =》fix high variance(underfit)
- 减少特征数量 =》fix high variance
- 获得额外的特征 =》fix high bias(overfit)
- 增加高维(组合)特征 =》fix high bias
- 增大 lambda =》fix high bias
- 减小 lambda =》fix high variance
- 机器学习诊断:
- 算法在什么样问题是work的或者不work的
- 需要耗时构建
- 指导提高模型的性能
- 模型评估:
- 训练集效果好(错误低),但是不能很好的在新数据集上。可能存在过拟合,低维(二维)可以直接画,但是对于多维数据不合适。
- 分训练集和测试集,训练集构造模型,在测试集上预测,评估模型效果。
- 模型选择:
- 对于不同的模型,构建训练集+验证集+测试集,前两者用于构建模型,测试集计算错误评估效果
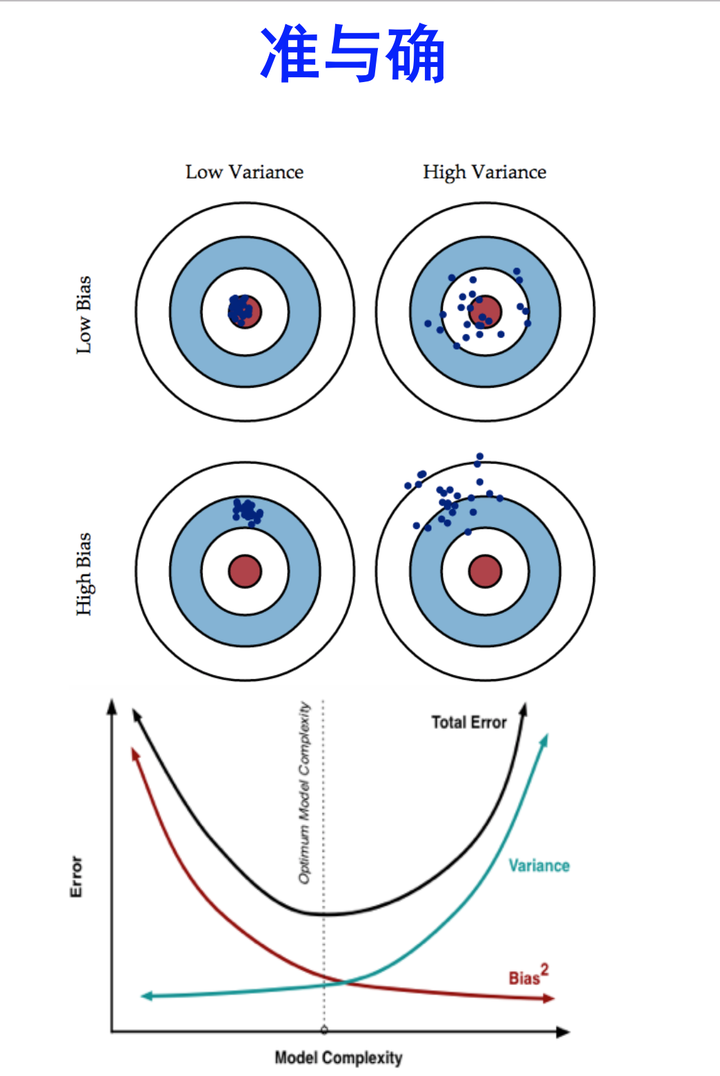
- 模型高偏差(bias)还是高差异(variance):
- high bias:underfit,比如在训练集和验证集上错误都很高,且两者很接近。
- high variance:overfit,比如在训练集上错误很低,但是在验证集上错误很高。
- 正则化与bias、variance:
- 正则化参数:lambda(平衡模型的性能和复杂度)
- 小的lambda,模型很复杂,可能会overfit,high variance
- 大的lambda,效果不很好,可能是underfit,high bias
- 选择不同的lambda值,起到正则化的效果,控制模型的复杂度。用训练集、验证集和测试集的错误值,选取合适的lambda值。
- 学习曲线(learning curve):
- 根据学习曲线判断如何提高模型的效果
- 学习曲线: 样本数量 vs 模型在训练集和验证集上的错误(error)
- 如果是模型high bias(underfit),训练集的误差随样本量增大逐渐增大到平稳,验证集的误差随样本量增大逐渐减小到平稳。【用更多的训练数据不会提升效果】
- 如果模型是high variance(overfit),【用更多的训练数据会提升效果】
- 神经网络和过拟合:
- 小网络:少的参数,容易欠拟合
- 大网络:多的参数,容易过拟合(模型太复杂,不易推广到新的数据)
- 大网络的过拟合可解决方式:正则化
- 知乎:Bias(偏差),Error(误差),和Variance(方差):
11: Machine Learning System Design
- 垃圾邮件检测:
- 监督学习:单词作为特征
- 收集数据,email头信息提取特征,正文信息提取特征,错误拼写检测
- 误差分析:
- 实现简单模型,测试在验证数据集上的效果
- 画学习曲线,看数据量、增添特征能否提升模型性能
- 误差分析:focus那些预测错误的样本,看是否有什么明显的趋势或者共同特征?
- 分析需要在验证数据集上,不是测试集上
- skewd class的误差分析:
- precision: # true positive / # predicted positive = # true positive / (# true positive + # false positive)
- recall: # true positive / # actual positive = # true positive / (# true positive + # false negative)
- F1 score = 2 * (Precision * Recall) / (Precision + Recall)
- 在验证数据集上,计算F1 score,并使其最大化,对应于模型效果最佳
- large data rationale: 可以构建有更多参数的模型
12: Support Vector Machines
13: Clustering
14: Dimensionality Reduction
15: Anomaly Detection
- 异常检测:主要用于非监督学习问题。根据很多样本及其特征,鉴定可能异常的样本,比如产品出厂前进行质量控制测试(QA)。
- 对于给定的正常数据集,想知道一个新的数据是不是异常的,即这个测试数据不属于该组数据的几率,比如在某个范围内概率很大(正常样本),范围之外的几率很小(异常样本),这种属于密度估计。
- 高斯分布:常见的一个分布,刻画特征的情况:
- 两个参数:期望和方差
- 利用高斯分布进行异常检测:
- 对于给定数据集,对每一个特征计算高斯分布的期望和方差(知道了每个特征的密度分布函数)
- 对新数据集,基于所有特征的密度分布,计算属于此数据集的概率
- 当计算的P小于ε时,为异常。(这个ε怎么定?)
- 开发和评估:
- 异常检测系统,先从带标记的数据选取部分构建训练集,获得概率分布模型;然后用剩下的正样本和异常数据构建交叉检验集和测试集。
- 测试集:估计每个特征的平均值和方差,构建概率计算函数
- 检验集:使用不同的ε作为阈值,看模型的效果。主要用来确定模型的效果,具体就是ε值大小。
- 测试集:用选定的ε阈值,针对测试集,计算异常检验系统的F1值等。
- 注意1:数据。训练集只有正常样本(label为0),但是为了评估系统性能,需要异常样本(label为1)。所以需要一批label的样本。
- 注意2:评估。正负样本严重不均衡,不能使用简单的错误率来评估(skewed class),需要用precision、recal、F-measure等度量。
- 异常检测 vs 监督学习:
- 数据量:前者负样本(异常的)很多
- 数据分布:异常检测的负样本(正常样本)分布很均匀,认为服从高斯分布,但是正样本是各种各样的(不正常的各有各的奇葩之处)
- 模型训练:鉴于异常样本的数量少,且不均匀,所以不能用于算法学习。所以异常样本:不参与训练,没有参与高斯模型拟合,只是在验证集和测试集中进行模型的评估。
- 特征选择(转换):
- 特征不服从高斯分布,异常检测算法也可以工作
- 最好转换为高斯分布:比如对数函数变换 =》x=log(x+c)
- 比如在某一维度时,某个样本对应的概率处于正常和异常的附近,很可能判断错误,可以通过查看其在其他维度(特征)的信息,以确定其是否异常。
- 误差分析:
- 问题:异常的数据有较高的P(x)值,被认为是正常的
- 只看被错误检测为正常的异常样本,看是否需要增加其他的特征,以检测这部分异常
- 多元高斯分布:
- 一般高斯计算P(x): 分别计算每个特征对应的几率然后将其累乘起来
- 多元高斯计算P(x): 构建特征的协方差矩阵,用所有的特征一起来计算
- 问题:一般高斯的判定边界比较大,有时候会把样本中的异常分布判定为正常样本
- 协方差举证对高斯分布的影响:
- 一般高斯 vs 多元高斯:
- 应用多元高斯构建异常检测系统:
- 原始模型 vs 多元高斯模型:
- 以上参考这里的学习笔记
16: Recommender Systems
17: Large Scale Machine Learning
18: Application Example - Photo OCR
19: Course Summary
If you link this blog, please refer to this page, thanks!
Post link:https://tsinghua-gongjing.github.io/posts/CS229-notes.html
Previous:
sklearn: 模型评估与选择
Next:
Xgboost
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me