Home > MachineLearning > Main text

K均值聚类算法

Tag: python, machine learning
2018-09-02

目录

聚类的含义和类型

聚类（clustering）：将相似的对象归到同一个簇中，将不相似对象归到不同簇，有点像全自动分类，是一种无监督的学习。sklearn提供了一个常见聚类算法的比较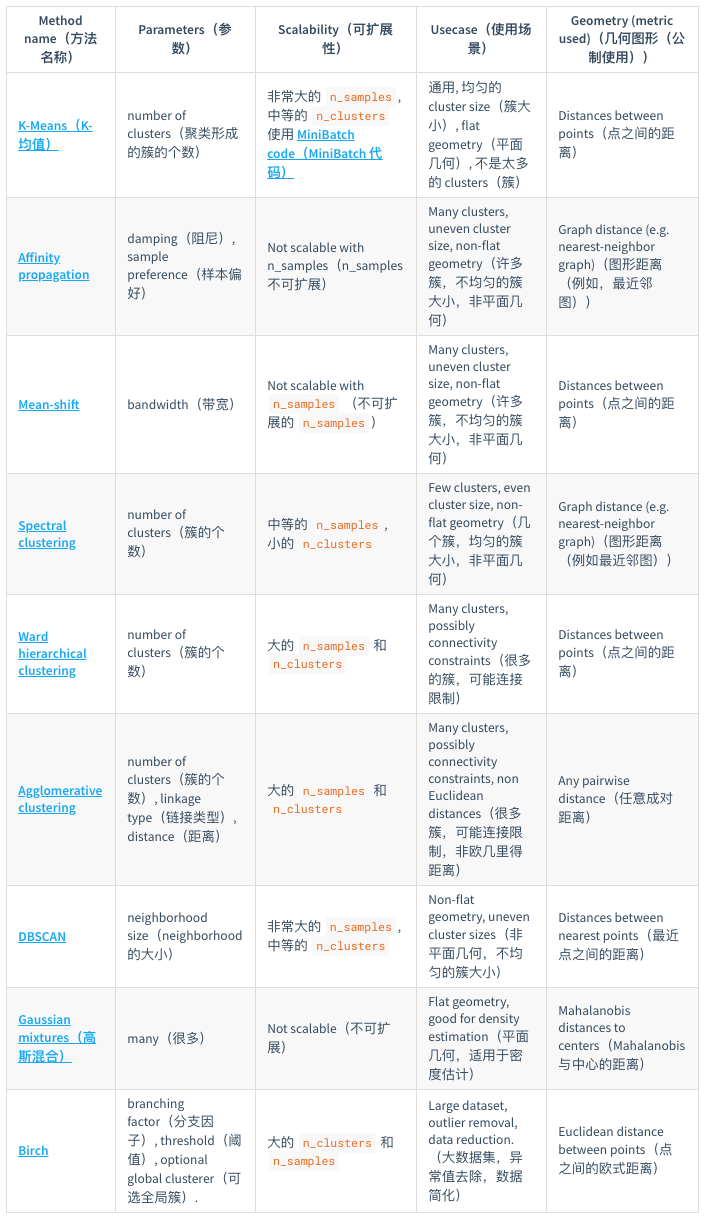：sklearn_clustering_comparison.png

k-均值聚类

  1. K-均值聚类（K-means clustering）：发现k个不同的簇，且每个簇的中心采用簇中所含值的均值计算而成（因此成为K-均值）。
  2. 簇识别（cluster identification）：给出聚类结果的含义。
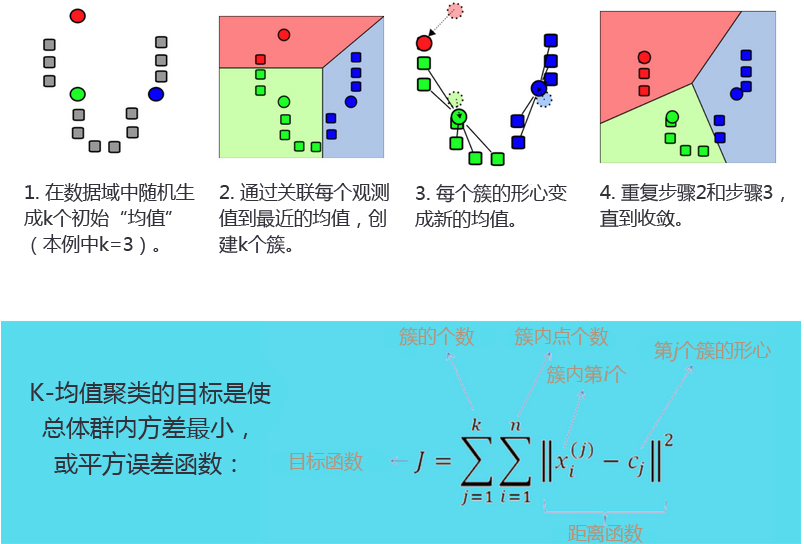
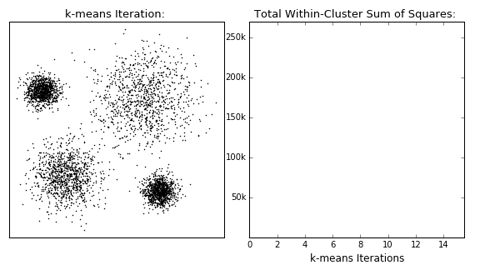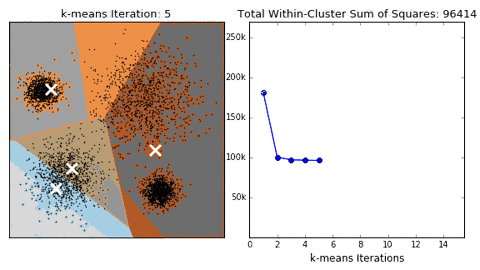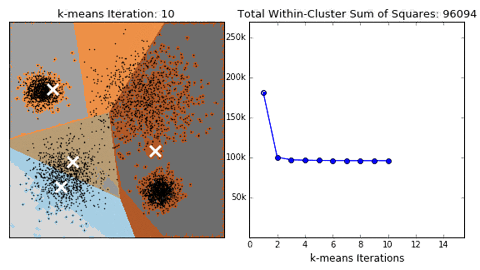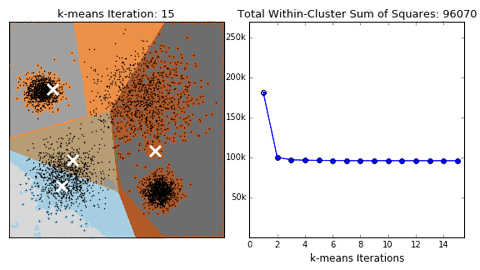
  3. K-均值聚类过程：
    • 过程如下：1）随机初始化簇中心；2）所有点分配到最近的簇中心；3）更新簇中心；重复2）和3）直到收敛。
    • 优化目标：可采用误差平方和，误差可用不同的距离比如欧式距离等。kmeas_steps_loss_function.png
    • 下面是一个动态的演示：最初设定分为4个类，经过簇中心初始化，不断的迭代，直到收敛。左边是点的分类的变化，右边是每次迭代的目标函数值的变化，当模型收敛时，损失值基本不变。

K-均值聚类的后处理

  • 可能提高分类性能
  • k的选择是否正确？误差和可用于评估聚类质量
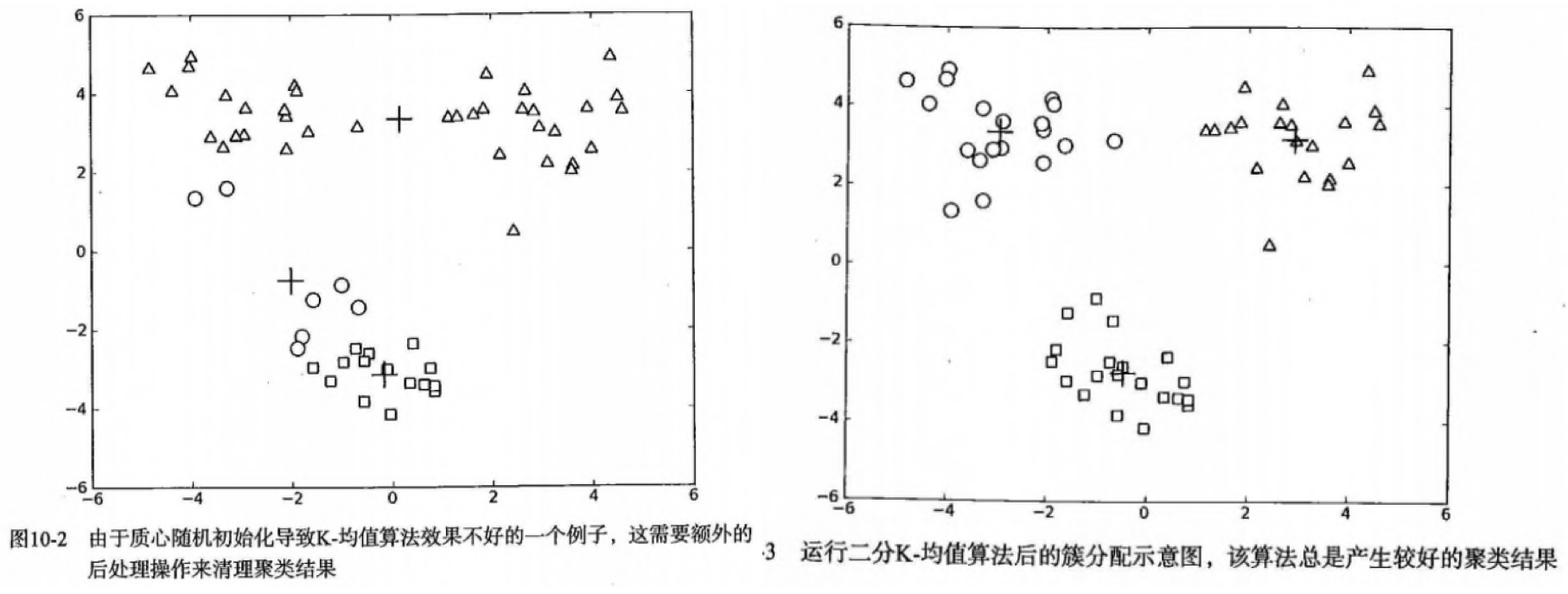
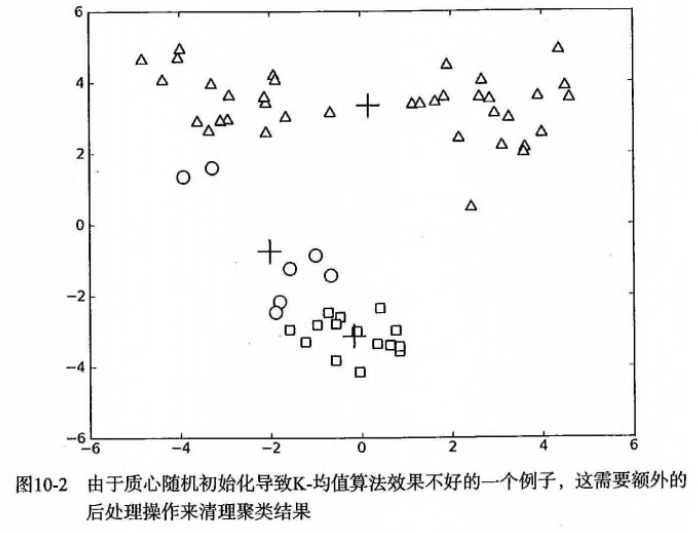
  • 问题：聚类结果可能不准确，收敛于局部最优，而非全局最优。下面是一个例子：kmeans_random_centroid.png
  • 方案1：多尝试不同的随机初始化中心，看结果是否一致。【初始化的随机性会对结果产生影响】
  • 方案2（二维）：人为合并簇，比如上图中下面的两个簇（圆圈+方块）
  • 方案2（高维）：1）合并最近的质心，2）合并两个使得SSE增幅最小的质心。

二分K-均值聚类

  • 二分K-均值（bisecting K-means）：克服K-均值算法收敛于局部最小的问题
  • 过程：1）将所有点看成一个簇，2）当簇数目小于指定数k时，对每个簇：计算总误差，进行k-均值聚类（k=2），计算将该簇一分为二后的总误差，3）选择使得误差最小的那个簇进行划分操作。
  • 上面第（3）步是选择使得误差最小的那个簇进行划分操作。，也可以是所对误差平方和最大的簇（似乎更容易理解）进行再一次的划分，因为误差平方和越大，表示该簇聚类越不好，越有可能是多个簇被当成一个簇了，所以我们首先需要对这个簇进行划分。
  • 属于层次聚类的一种，是分裂的想法：先是所有的都属于一类，再慢慢的分为更细的不同的类别。
  • 效果：运行多次后会收敛到全局最小，比如在上面的数据集中效果更好。kmeans_vs_bisectkmeans.png

Python源码版本

K-均值聚类：

def distEclud(vecA, vecB):
	""" 计算两数据点之间的距离，这里是欧式距离
	"""
    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)

def randCent(dataSet, k):
	""" 随机初始化选取k个中心，注意这些点不是原来有的数据点
	"""
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))#create centroid mat
    for j in range(n):#create random cluster centers, within bounds of each dimension
        minJ = min(dataSet[:,j]) 
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
    return centroids
    
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))#create mat to assign data points 
                                      #to a centroid, also holds SE of each point
    centroids = createCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):#for each data point assign it to the closest centroid
            minDist = inf; minIndex = -1
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2
        print centroids
        for cent in range(k):#recalculate centroids
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster
            centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean 
    return centroids, clusterAssment

二分 K-均值聚类：

def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))
    centroid0 = mean(dataSet, axis=0).tolist()[0]
    centList =[centroid0] #create a list with one centroid
    for j in range(m):#calc initial Error
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
    while (len(centList) < k):
        lowestSSE = inf
        for i in range(len(centList)):
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
            sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
            print "sseSplit, and notSplit: ",sseSplit,sseNotSplit
            if (sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        print 'the bestCentToSplit is: ',bestCentToSplit
        print 'the len of bestClustAss is: ', len(bestClustAss)
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids 
        centList.append(bestNewCents[1,:].tolist()[0])
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE
    return mat(centList), clusterAssment

sklearn版本

对二维数据点进行聚类：

from sklearn.cluster import KMeans
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],
              [10, 2], [10, 4], [10, 0]])
kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
kmeans.labels_
# array([1, 1, 1, 0, 0, 0], dtype=int32)

kmeans.predict([[0, 0], [12, 3]])
# array([1, 0], dtype=int32)

kmeans.cluster_centers_
# array([[10.,  2.],
#       [ 1.,  2.]])

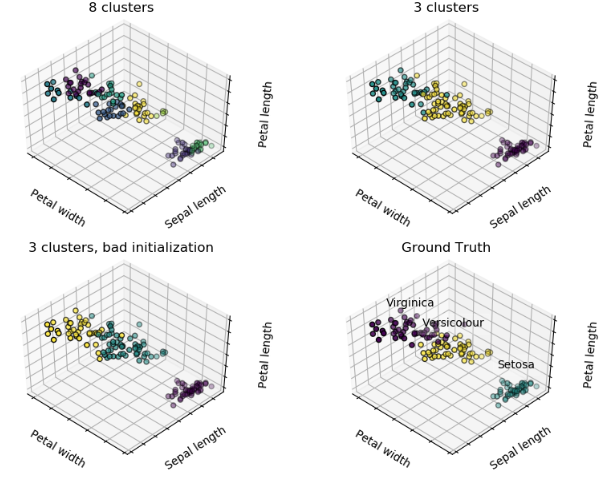
对iris数据集进行聚类并与真实的进行可视化比较：

# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt
# Though the following import is not directly being used, it is required
# for 3D projection to work
from mpl_toolkits.mplot3d import Axes3D

from sklearn.cluster import KMeans
from sklearn import datasets

np.random.seed(5)

iris = datasets.load_iris()
X = iris.data
y = iris.target

estimators = [('k_means_iris_8', KMeans(n_clusters=8)),
              ('k_means_iris_3', KMeans(n_clusters=3)),
              ('k_means_iris_bad_init', KMeans(n_clusters=3, n_init=1,
                                               init='random'))]

fignum = 1
titles = ['8 clusters', '3 clusters', '3 clusters, bad initialization']
for name, est in estimators:
    fig = plt.figure(fignum, figsize=(4, 3))
    ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
    est.fit(X)
    labels = est.labels_

    ax.scatter(X[:, 3], X[:, 0], X[:, 2],
               c=labels.astype(np.float), edgecolor='k')

    ax.w_xaxis.set_ticklabels([])
    ax.w_yaxis.set_ticklabels([])
    ax.w_zaxis.set_ticklabels([])
    ax.set_xlabel('Petal width')
    ax.set_ylabel('Sepal length')
    ax.set_zlabel('Petal length')
    ax.set_title(titles[fignum - 1])
    ax.dist = 12
    fignum = fignum + 1

# Plot the ground truth
fig = plt.figure(fignum, figsize=(4, 3))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)

for name, label in [('Setosa', 0),
                    ('Versicolour', 1),
                    ('Virginica', 2)]:
    ax.text3D(X[y == label, 3].mean(),
              X[y == label, 0].mean(),
              X[y == label, 2].mean() + 2, name,
              horizontalalignment='center',
              bbox=dict(alpha=.2, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y, edgecolor='k')

ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title('Ground Truth')
ax.dist = 12

fig.show()

kmeans_demo_iris.png

选择合适的K，可参考这里：

from sklearn.cluster import KMeans
from sklearn import metrics
from nested_dict import nested_dict

silhouette_score_dict = nested_dict(1, int)
for k in range(3, 15):
    kmeans_model = KMeans(n_clusters=k, random_state=0).fit(df_select_01)
    silhouette_score = metrics.silhouette_score(df_select_01, kmeans_model.labels_,metric='euclidean')
    print(k, silhouette_score)
    silhouette_score_dict[k] = silhouette_score

参考


If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/K-means.html
Previous: 树回归算法

    Category

    Latest articles

    Links