概率：

1. 被赋予概率的“事情”称为事件（event）。如果E表示一个事件，那么P(E)就表示该事件发生的概率。检测E发生情况的过程就叫做试验（trial）。
2. 频率论（frequentism）：用频率来定义概率。如果没有一系列相同的试验，那就不存在概率。
3. 贝叶斯认识论（bayesianism）：将概率定义为事件发生的可信度，适用范围更广，但是更主观。
4. 概率法则：1）P(AB)=P(A)P(B)，A/B需要相互独立；2）条件概率P(A\∣B)=P(A|B)P(A∣B)，A/B不相互独立时；3）由前面归纳一个公式：P(AB)=P(A)P(B∣A)，不论A/B独立与否都适用。
5. 蒙提霍尔问题：假设你正在参加一个游戏节目，你被要求在三扇门中选择一扇：其中一扇后面有一辆车；其余两扇后面则是山羊。你选择了一道门，假设是一号门，然后知道门后面有什么的主持人，开启了另一扇后面有山羊的门，假设是三号门。他然后问你：“你想选择二号门吗？”转换你的选择对你来说是一种优势吗？ 答案是：转换选择能够提升获胜概率。
6. 二项分布：n是试验总次数，p是成功的概率，k是成功的次数。

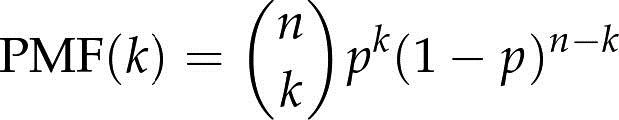
1. 连胜：不存在连胜或者连败。
2. 聚类错觉（clustering illusion）：指看上去好像有某种特点的聚类实际上是随机的。可通过蒙特卡洛模拟，看随机情况产生类似聚类的概率。
3. 贝叶斯定理（Bayes’s theorem）描述的是两个事件的条件概率之间的关系。条件概率通常写成P(A|B)，表示的是在事件B已发生的情况下事件A发生的概率。P(H\∣E)=P(H)P(E\∣H)/P(E):在看到E之后H的概率P(H|E)，等于看到该证据前H的概率P(H)，乘以假设H为真的情况下看到该证据的概率P(E|H)与在任何情况下看到该证据的概率P(E)的比值P(E|H)/P(E)。

术语：

• 贝叶斯认识论（Bayesianism） 一种对概率更泛化的解释，用概率表示可信的程度。
• 变异系数（coefficient of variation） 度量数据分散程度的统计量，按集中趋势归一化，用于比较不同均值的分布。
• 事件（event） 按一定概率发生的事情。
• 失败（failure） 事件没有发生的试验。
• 频率论（frequentism） 对概率的一种严格解读，认为概率只能用于一系列完全相同的试验。
• 独立（independent） 若两个事件之间相互没有影响，就称这两个事件是独立的。
• 证据的似然值（likelihood of the evidence） 贝叶斯定理中的一个概念，表示假设成立的情况下看到该证据的概率。
• 蒙特卡罗模拟（Monte Carlo simulation） 通过模拟随机过程计算概率的方法（详见http://wikipedia.org/wiki/Monte_Carlo_method）。
• 归一化常量（normalizing constant） 贝叶斯定理中的分母，用于将计算结果归一化为概率。
• 后验（posterior） 贝叶斯更新后计算出的概率。
• 先验（prior） 贝叶斯更新前计算出的概率。
• 成功（success） 事件发生了的试验。
• 试验（trial） 对一系列事件是否可能发生的尝试。
• 更新（update）** 用数据修改概率的过程。