目录

• 目录
• 聚类任务
• 聚类结果的性能度量
  • 度量：外部指标
  • 度量：内部指标
• 距离计算
• 原型聚类
  • k-均值聚类
  • 学习向量量化聚类
  • 高斯混合聚类
• 密度聚类
  • DBSCAN
• 层次聚类
  • AGNES
• 参考

---

聚类任务

1. 无监督学习任务
   • 聚类（clustering）
   • 密度估计（density estimation）
   • 异常检测（anomaly detection）
2. 聚类
   • 将数据集中的样本划分为若干个不想交的子集，每个子集称为一个簇（cluster）
   • 可做为单独过程：寻找数据内在的分布结构
   • 其他学习任务的前驱过程
   • sklearn提供的常见聚类算法：

---

聚类结果的性能度量

1. 性能度量：有效性指标（validity index），类似于监督学习中的性能度量
2. 什么样的类好？
   • 直观：物以类聚
   • 归纳：簇内(intra-cluster)相似度高而簇间(inter-cluster)相似度低
3. 度量分类：
   • 外部指标：external index，将聚类结果与某个参考模型进行比较
   • 内部指标：internal index，直接考察聚类结果而不利用任何参考模型
   • F值
   • 互信息：mutual information
   • 平均廓宽：average silhouette width

---

度量：外部指标

定义：

• 数据集：\(D={x_1,x_2,...,x_n}\)
• 聚类结果的簇划分：\(C={C_1,C_2,...,C_n}\)
• 参考模型的簇划分：\(C^*={C^*_1,C^*_2,...,C^*_n}\)
• \(C\)的簇标记向量
• \(C^*\)的簇标记向量

---

度量：内部指标

---

距离计算

• 距离度量：样本之间的距离
• 基本性质：
  • 非负性：\(dist(x_i,x_j) \geq 0\)
  • 同一性：\(dist(x_i,x_j)=0,当且仅当x_i=x_j\)
  • 对称性：\(dist(x_i,x_j)=dist(x_j,x_i)\)
  • 直递性：\(dist(x_i,x_j) \leq dist(x_i,x_k)dist(x_k,x_j)\)
• 不同的度量：
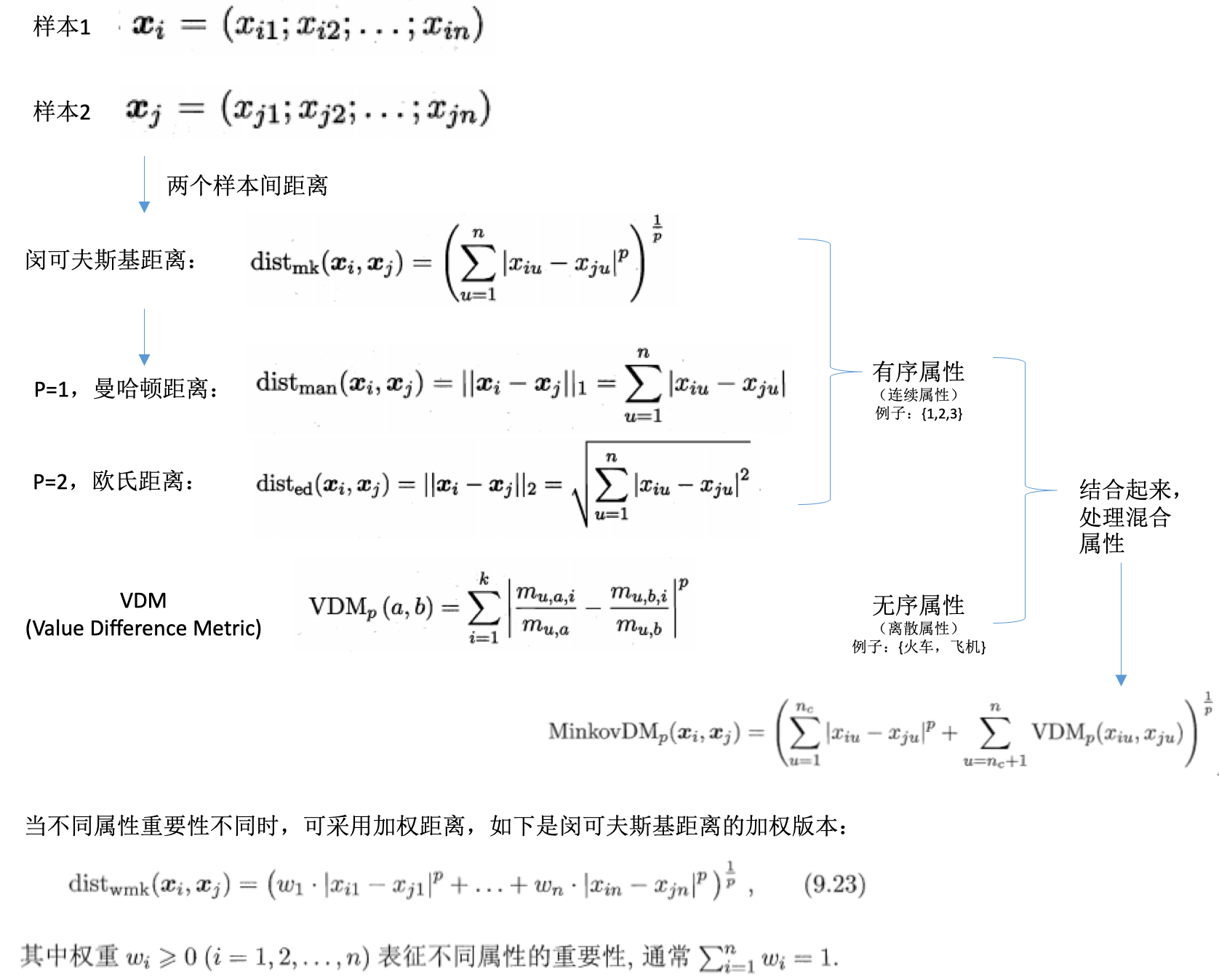
• 还有其他的距离计算方式，比如：
  • 內积距离
  • 余弦距离

---

原型聚类

• 原型聚类：基于原型的聚类（prototype-based clustering）
• 原型：样本空间中具有代表性的点
• 基础：假设聚类结构能通过一组原型刻画

---

k-均值聚类

详细请参见另一篇博文K均值聚类算法，其算法流程如下：

---

学习向量量化聚类

• 学习向量量化：Learning Vector Quantization, LVQ
• 类似于k均值，寻找一组原型向量
• 但是是假设数据样本带有类别标记，学习的过程中会使用这些标记以辅助聚类

---

高斯混合聚类

• k均值、LVQ：使用原型向量
• 高斯混合：mixture of gaussian，采用概率模型来表达聚类原型，而非向量

---

密度聚类

• 密度聚类：density-based clustering
• 基础：假设聚类结构能通过样本分布的紧密程度确定
• 样本密度 -》样本的可连接性，基于可连接样本扩展聚类簇，得到最终聚类结果
• 聚类方法：
  • DBSCAN
  • OPTICS
  • DIANA：自顶向下

DBSCAN

• density-based spatial clustering of applications with noise
• 基于邻域参数刻画样本分布的紧密程度
• 概念：

• 算法流程如下：

---

层次聚类

• 层次聚类：hierarchical clustering
• 在不同层次对数据集进行划分，从而形成树形的聚类结构
• 聚合策略：自低向上
• 分拆策略：自顶向下

AGNES

• AGNES：AGglomerative NESting

• 自底向上的聚合策略

• 每个样本看成一个簇
• 找出距离最近的两个簇进行合并

• 不断重复，直到达到预设的聚类簇的个数

• 关键：如何计算簇之间的距离。上面介绍的是计算样本之间的距离。
• 簇间距离计算：
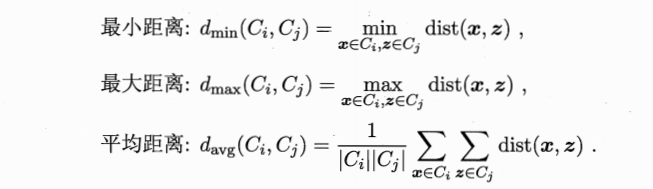
• 可选择不同的距离计算方式
  • 最小距离：两个簇的最近样本决定，单链接（single-linkage）
  • 最大距离：两个簇的最远样本决定，全链接（complete-linkage）。所以我们通常使用的是全链接，是最大的距离？
  • 平均距离：两个簇的所有样本决定，均链接（average-linkage）
• 算法流程：

---

参考

• 机器学习周志华第9章

If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/clustering.html

Previous: Think Stats: probability