• 动态规划算法的启示
• 最长公共子串
• 最长公共子序列
• 代码实现
• DP其他应用
• 参考

动态规划算法的启示

• 能在给定约束条件下找到最优解。背包问题：在背包容量下。
• 问题可分解为彼此独立且离散的子问题时
• 提出DP方案：
  • 每种DP解决方案都涉及网格
  • 单元格中的值通常就是要优化的值
  • 每一个单元格都是一个子问题，因此应该考虑如何将问题分成子问题

最长公共子串

• 给定串中任意个连续的字符组成的子序列称为该串的子串，longest common substring
• 问题：一个字典查询网站，用户输入hish，但是有两个类似的词fish、vista，判断用户应该是输入的哪一个？
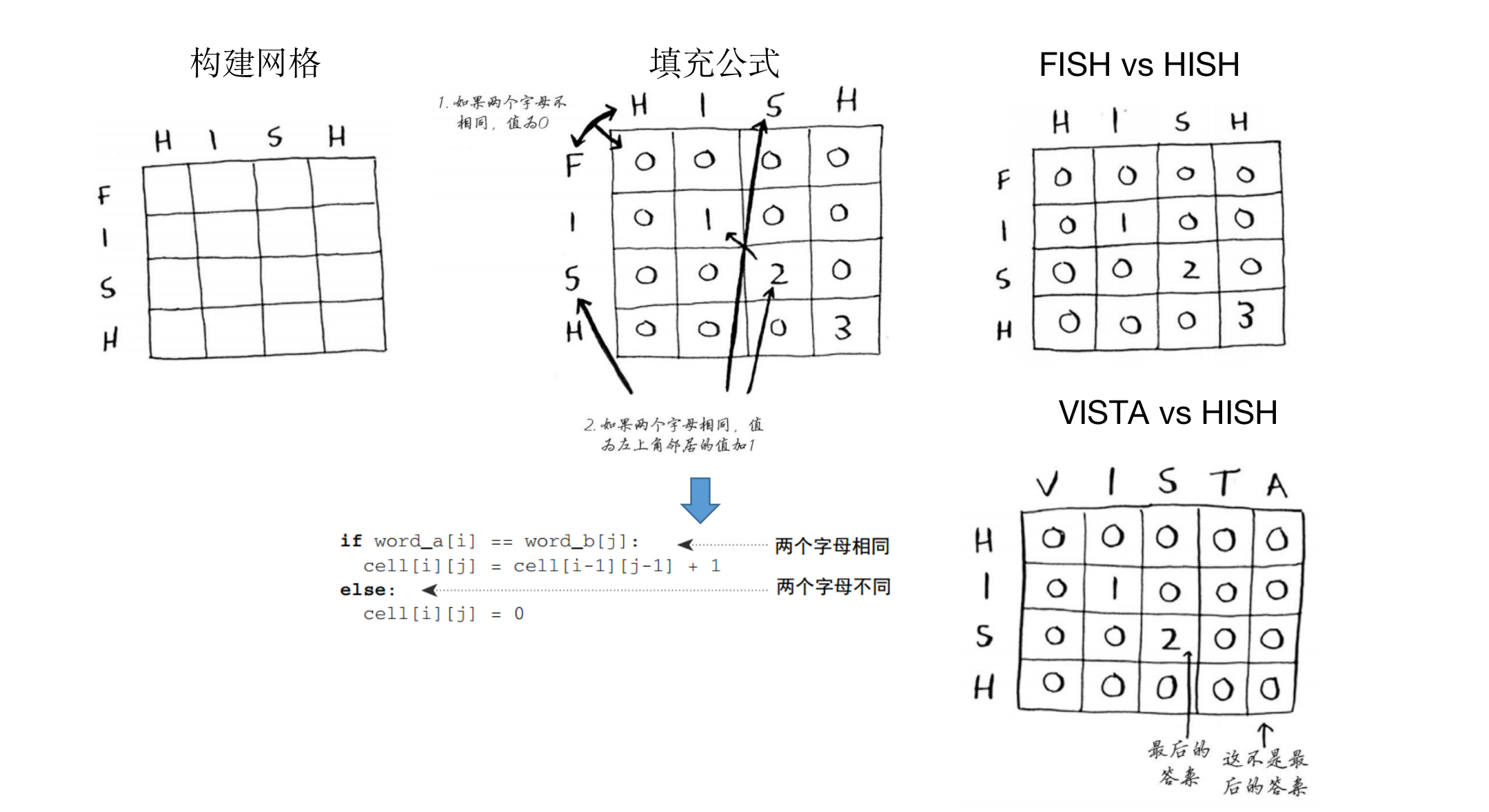
• 绘制网格：
  • 单元格中的值是什么？
  • 如何将这个问题划分为子问题？
  • 网格的坐标轴是什么？
• 填充表格：
  • 填充值的公式是什么？
  • 没有固定的公式，需要自行摸索。比如上面的背包问题公式，并不是通用的。
• 答案：
  • 背包：最后的单元格值是的
  • 最长公共子串：网格中的最大数字，可能不是位于最后的单元格中

最长公共子序列

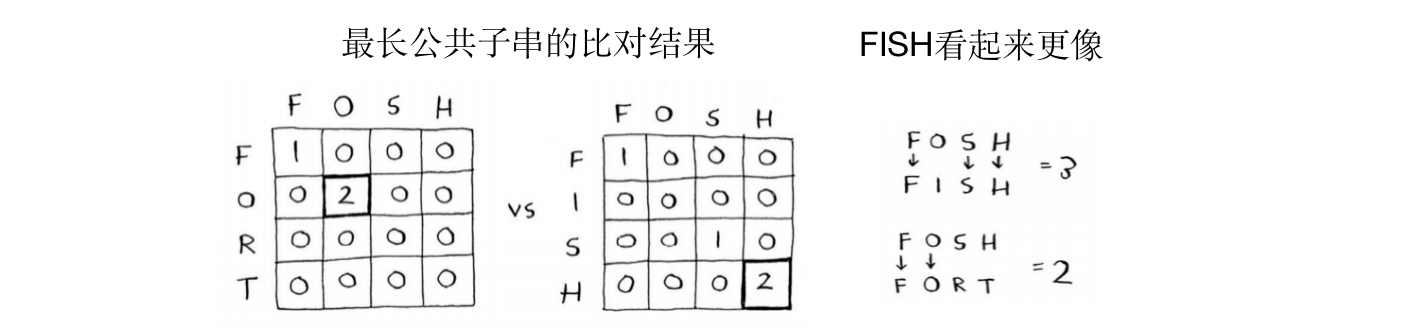
• 问题：用户输入的是fosh，那么其是想输入fish还是fort呢？
• 最长公共子串：
  • 结果相同，都为2
  • 但是明显FISH是更接近的，因为有3个字符是相同的
• 最长公共子序列：
  • 两个单词中都有的序列包含的字母数，longest common sequence
  • appears in the same relative order, but not necessarily contiguous，将给定序列中零个或多个元素去掉之后得到的结果
  • “abc”, “abg”, “bdf”, “aeg”, ‘”acefg”, 等等都是“abcdefg”的子序列
  • 复杂度：长度为n的字符串，其子序列共有2^n种
  • 所以比如F是FOSH、FISH都包括的，即使和后面的SH不相连，也应该计算在内
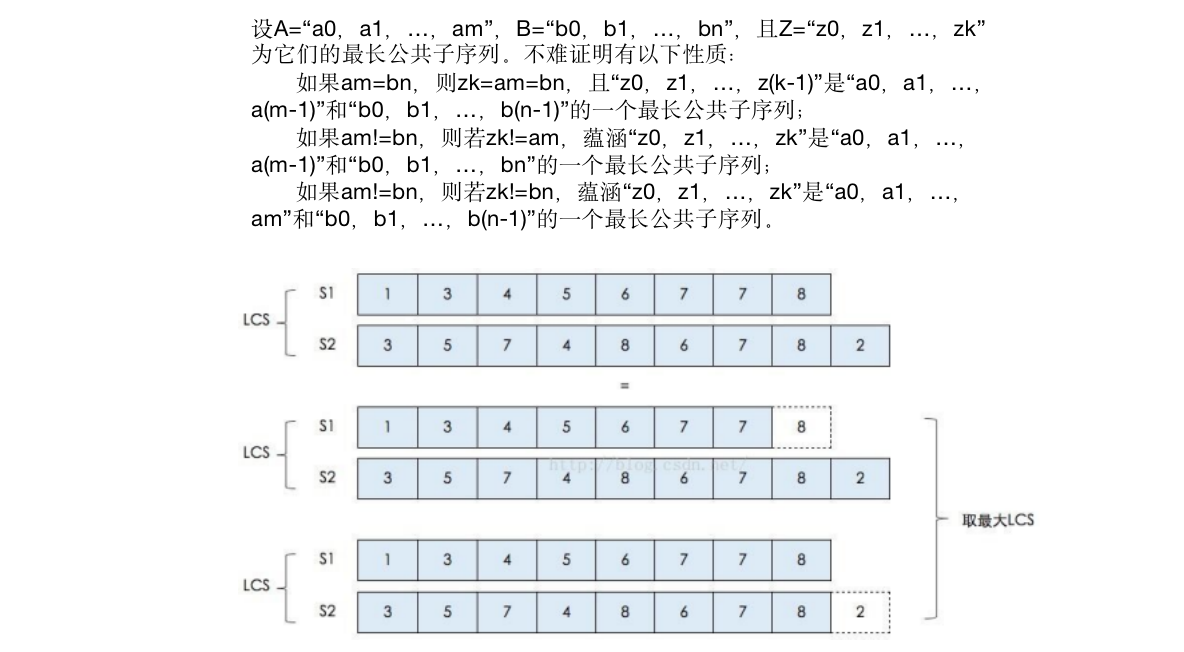
  • 计算公式推导：
  • 网格流程：
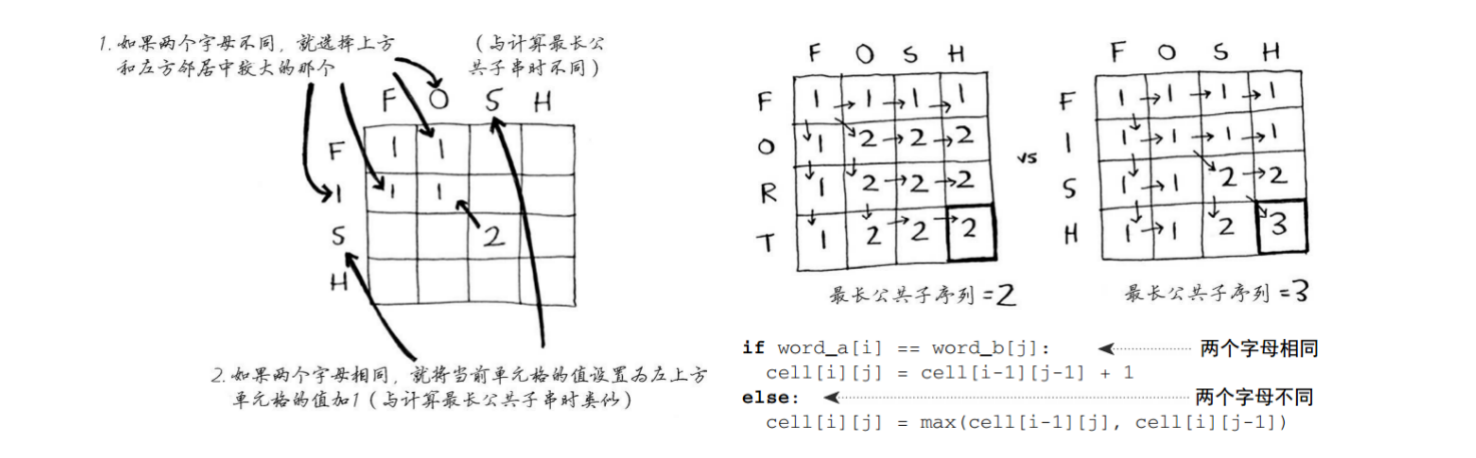
• 下面是一个数字字符串的比对流程：
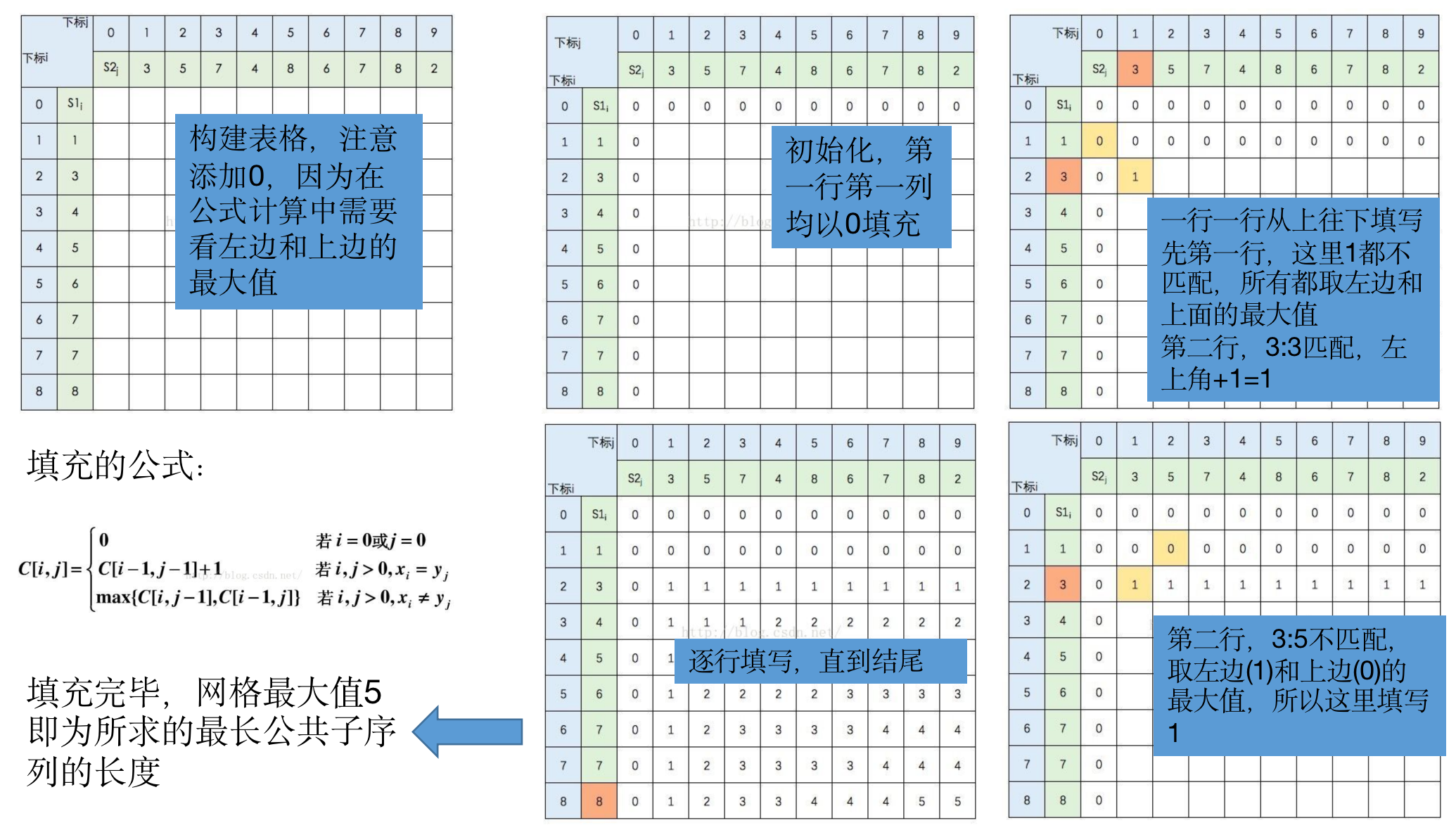
• 回溯：
  • 从最后一个格子开始
  • 如果格子对应的x值和y值相等，则可知这个值是左上角值+1的得来的
  • 如果格子对应的x值和y值不相等，则可知这个值是从上边或者左边的最大值来的
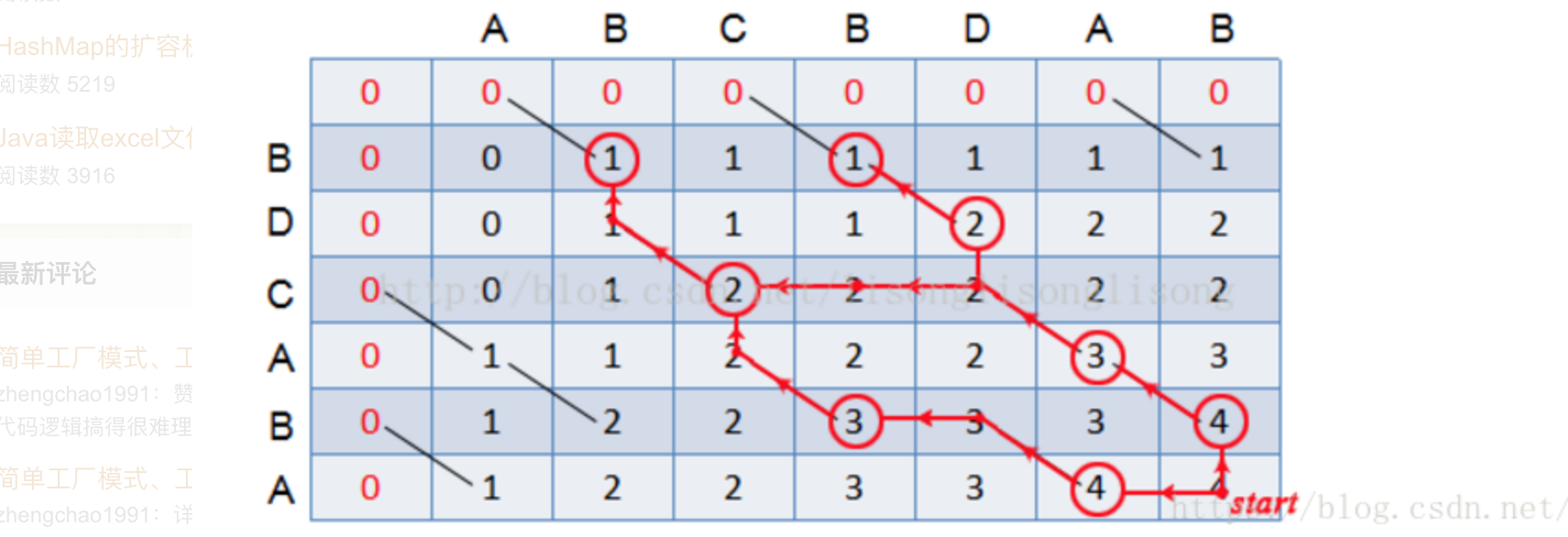
    • 如果上边和左边值是相等的，则选择其中一个。当选择了一个方向之后，后面如果碰到相等的情况，也使用相同的方向回溯。

代码实现

递归实现：

# A Naive recursive Python implementation of LCS problem 

# X: string1, Y: string2
# m: len(X), n: len(Y)

def lcs(X, Y, m, n): 

	if m == 0 or n == 0: 
		return 0; 
	elif X[m-1] == Y[n-1]: 
		return 1 + lcs(X, Y, m-1, n-1); 
	else: 
		return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)); 


# Driver program to test the above function 
X = "AGGTAB"
Y = "GXTXAYB"
print "Length of LCS is ", lcs(X, Y, len(X), len(Y)) 

# Length of LCS is  4

Dynamic programming 实现：

# Dynamic Programming implementation of LCS problem 

def lcs(X, Y): 
	# find the length of the strings 
	m = len(X) 
	n = len(Y) 

	# declaring the array for storing the dp values 
	L = [[None]*(n + 1) for i in xrange(m + 1)] 

	"""Following steps build L[m + 1][n + 1] in bottom up fashion 
	Note: L[i][j] contains length of LCS of X[0..i-1] 
	and Y[0..j-1]"""
	for i in range(m + 1): 
		for j in range(n + 1): 
			if i == 0 or j == 0 : 
				L[i][j] = 0
			elif X[i-1] == Y[j-1]: 
				L[i][j] = L[i-1][j-1]+1
			else: 
				L[i][j] = max(L[i-1][j], L[i][j-1]) 

	# L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] 
	return L[m][n] 
# end of function lcs 


# Driver program to test the above function 
X = "AGGTAB"
Y = "GXTXAYB"
print "Length of LCS is ", lcs(X, Y) 

# This code is contributed by Nikhil Kumar Singh(nickzuck_007) 

# Length of LCS is  4

DP其他应用

• DNA序列之间的相似性，从而确定物种相似性
• git diff命令找两个文件的差异
• 编辑距离：两个字符串的相似程度，拼写检查，用户上传的资料是否为盗版
• word的断字功能，判断在什么地方断字以保证行长一致

参考

• 图解算法第九章
• Python Program for Longest Common Subsequence
• 动态规划 最长公共子序列 过程图解