Home > MachineLearning > Main text

Google machine learning

Tag: python, machine learning, google
2018-03-06

最近，google在其开发网站上，公开了用于内部人员进行机器学习培训的材料，可以快速帮助了解机器学习及其框架TensorFlow。量子位提供了一个相关材料的连接（别翻墙了，谷歌机器学习速成课25讲视频全集在此）。近期会学习这个系列的材料，做一点后续的笔记。

课程概览

机器学习概念

简介

框架处理

  1. 介绍了基本框架（监督式机器学习）和及一些术语
  2. 基本术语：
    • 标签：要预测的真实事物（y）
    • 特征：描述数据的输入变量（xi）。特征尽量是可量化的，比如鞋码、点击次数等，美观程度等不可量化，不适合作为特征。
    • 样本：数据的特定实例
    • 有标签样本：训练模型；无标签样本：对新数据做预测
  3. 模型：将样本映射到预测标签
    • 回归模型：预测连续值
    • 分类模型：预测离散值

深入了解机器学习

  1. 介绍了线性回归，房屋面积预测销售价格的例子，引出如何评价线性回归的好坏。
  2. 模型训练：通过有标签样本来学习（确定）所有权重和偏差的理想值
  3. 监督式学习（经验风险最小化）：检查多个样本并尝试找出可最大限度地减少损失的模型
  4. 损失：
    • L2loss（平方误差/平方损失）：预测值和标签值之差的平方
    • 均方误差 (MSE) ：每个样本的平均平方损失，平方损失之和/样本数量

降低损失

  1. 训练模型需要reducing loss，迭代方法很常用。
  2. 迭代：根据输入和模型的随机初始值计算损失值，然后更新模型参数值，不断循环，使得损失值达到最小（试错过程）。当损失不再变化或者变化极其缓慢，可以说模型区域收敛。
  3. 梯度下降：上述迭代过程存在更新模型参数的步骤，使用此方法快速寻找达到最小损失的参数（不可能把所有的参数都尝试一遍）。
  4. 梯度：损失曲线在对应参数处的梯度（偏导数：有大小和方向），负梯度是对应梯度下降的。
  5. 如何选取下一个点？
    • 下降梯度值 x 学习速率（步长）
  6. 如果知道损失函数梯度较小，可以使用较大的学习速率，以较快的达到最小损失。
  7. 优化学习速率，理解通过调节不同的速率，使得学习效率能够收敛达到最高。在降低损失的方向选取小步长（因为想要精准的达到最低损失）。小步长：梯度步长。这种优化策略：梯度下降法。
  8. 权重初始化：凸形问题，可任意点开始，因为只有一个最低点；非凸形：有多个最低点，很大程度决定于起始值。
  9. 批量：单次迭代中计算梯度的样本总数。一般是总的样本，但是海量数据过于庞大。
  10. 随机梯度下降（SGD）：一次抽取一个样本
  11. 小批量梯度下降：每批10-1000个样本，使得估算均值接近整体，且计算时间可接受
  12. 关于理解梯度下降，机器之心翻译了一篇浅显易懂！「高中数学」读懂梯度下降的数学原理，来源于towarddatascience：
    • 梯度下降的公式：
    • 成本函数 vs 损失函数：损失函数是单个训练样本的误差，成本函数则是损失函数在整个训练集上的平均。
    • 任何机器学习算法的目标都是最小化成本函数。（实际值与预测值之间的误差越低，算法越好）
    • 求导幂规则：
    • 求导链式规则：

使用TF的基本步骤

  1. TF(TensorFlow) API(建议从高级API开始使用):
    • 面向对象的高级API：estimator
    • 库：tf.layers, tf.losses, tf.metrics
    • 可封装C++内核的指令：TensorFlow python/C++
    • 多平台：CPU/GPU/TPU
  2. TF线性回归：
# tf.estimator API

import tensorflow as tf

# set up a classifier
classifier = tf.estimator.LinearClassifier()

# Train the model on some example data.
# what does steps mean here?
classifier.train(input_fn=train_input_fn, steps=2000)

# Use it to predict.
predictions = classifier.predict(input_fn=predict_input_fn)
  1. 常用参数：
    • steps：训练迭代的总次数。一步计算一批样本产生的损失，然后使用该值修改模型权重
    • batch size：单步的样本数量，如SGD批次大小为1.
  2. 通过notebook介绍使用TF实现线性回归模型预测房屋价格

泛化

  1. 泛化（Generalization）：构建的模型拟合新数据的能力。希望是泛化能力强。
  2. 泛化能力弱的一个例子：过拟合。比如用复杂的非线性模型区分垃圾邮件，由于过拟合，对于新的邮件容易错误的标记为正常的或者垃圾邮件。
  3. 如何提高泛化能力？对数据样本进行抽样进行训练，同时用测试样本进行模型的测试（使用测试集方法，评估模型是否出色）。
  4. “奥卡姆剃刀”：模型应尽可能简单
  5. 这个做法基于3点：1）从分布中随机抽取独立同分布的样本；2）分布是平稳的（不会随时间变化）；3）始终从同一分布中抽取样本（包括训练集、验证集和测试集）
  6. 例子：比如购物行为在节假日和夏季不同（不平稳性），不同品种的小狗一样可爱（不是相同的分布）
  7. 如果某个模型不能很好地泛化到新数据，可能是过拟合了。如果已经通过测试集数据的方式进行模型训练了？还是过拟合的问题吗？

训练集和测试集

  1. 测试集：评估根据训练集开发的模型的数据集
  2. 陷阱：损失很低（效果很好，准确率100%） =》 检测是否不小心对测试数据进行了训练。
  3. 测试集条件：1）足够大（具有统计意义）；2）能代表整个数据集（特征与训练集相同）。
  4. 任务1：当测试损失值和训练损失值基本稳定时，其大小不存在明显差异（0.003，0.03，0.06，0.042，0.003）；任务2：学习速率3 -》1，损失差值边大；
  5. 任务1：当学习速率=3时，测试损失明显高于训练损失；任务2：如果降低学习速率，测试损失会减小，以接近于训练损失；任务3：降低训练样本比例，大幅减少训练样本个数。

验证

  1. 测试集的评估结果用于指导和调整模型参数（比如学习速率和特征），是否存在问题？多次重复会拟合特定的测试集，因为这里我们只对数据集进行了一次划分。
  2. 引入验证集：
    • 训练集+测试集：训练集训练 -》测试集评估 -》根据测试集效果调整 -》选择在测试集上的最佳模型。
    • 训练集+验证集+测试集：训练集训练 -》验证集评估 -》根据验证集效果调整 -》选择在验证集上的最佳模型 -》使用测试集确定效果。如果测试集效果和验证集效果不相当，则说明可能对于验证集进行了过拟合。有效防止过拟合是因为暴露给测试集的信息更少。

表示法

表示：Representation

  1. 选择最优代表性的数据特征集合
  2. 特征工程：从原始数据提取特征，占据75%的时间。
  3. 原始数据-》特征向量：
    • 映射数值：实值 =》数值(直接复制)，
    • 映射分类值：字符串 =》独热编码（比如编码ATCG四个碱基的，其中一个为1，其他均为0）转化为特征向量。
    • 原本可以顺序数字映射，比如不同地名映射为1，2，3。。。，但是这个涉及到权重问题，所以创建二元向量如[0,1,0,0,…]。独热编码：只有一个值为1；多热编码：多个值为1。
    • 稀疏表示法：假如有100万个街道，直接创建100万个元素的二元向量？低效！可采用稀疏表示法：仅存储非零值。
  4. 好特征：
    • 1）具有非零值且出现多次（否则应该被过滤掉）；
    • 2）具有明确清晰的定义，比如年龄不应该以秒来计算；
    • 3）不应使用“神奇”的值，比如某房屋没有出售可定义为-1；
    • 4）特征的定义不随时间变化（比如数据是从上游传来的，则可能发生变化），保证数据的平稳性；
    • 5）不包含离群值，可监测去除，也可采用分箱技术划分区间再进行独热编码；
  5. 了解数据：
    • 1）可视化；
    • 2）调试：重复样本、缺失值、离群值、与信息中心一致？训练数据与验证数据相似？
    • 3）监控：特征分位数、样本数量是否随着时间而变化？

  6. 检查数据：1）遗漏值；2）重复样本；3）不良标签；4）不良特征值。

  7. 数据清理：
    • 1）缩放特征值（标准化）：将浮点特征值从自然范围（例如 100 到900）转换为标准范围（例如 0 到 1 或 -1 到 +1）。好处：梯度下降法更快速地收敛；避免“NaN 陷阱”；3）为每个特征确定合适的权重。常规：Z-score线性缩放
    • 2）处理极端离群值：取对数；限定最大最小特征值（winsorazation）。
    • 3）分箱：比如房屋的纬度是浮点值，这个值与房屋出售价格没有线性关系。可以对纬度进行分区（分箱，用独热编码表示为多元二维向量），就可以把纬度的权重体现出来了。
  8. 特征集合编程练习：挑选特征，使得用极少的特征搭建简单的模型，效果和使用多个特征相当。
    • 良好特征集：相关矩阵（比如Pearson coefficient），探索以挑选独立的特征。不同的特征、不同的参数，是的损失不同。
    • 纬度：这种特征不直接，不能和其他feature或者结果直接相关，可进行转换。比如：1）latitude =》|latitude - 38|，38是洛杉矶的纬度，就转换为距离洛杉矶多远的地方；2）之前提过的分箱策略进行独热编码。

特征组合

  1. 特征组合（Feature Crosses）：两个或多个特征相乘。
  2. 合成特征（特征交叉）：[A x B]形式的，也可更加复杂[A x B x C x D x E]，注意这种得到的组合可能很稀疏，尤其是原来的特征是经过独热编码的时候。
  3. 例子：房价预测（维度 x 房间数目），井字游戏预测（位置1 x 位置2 x 位置3）
  4. 组合独热特征也很常见，比如结合小狗的行为（叫、依偎等的独热编码）和时间段（几点到几点的独热编码）来预测对于主人的满意程度。
  5. 为什么特征组合：
    • 虽然线性学习模型可扩展到大数据集，但是有些场景很受限制（预测效果不好）
    • 特征组合+大数据集 =》学习复杂模型（比如非线性模型）的有效策略
    • 神经网络也可以学习复杂模型
  6. Playground练习，很直观的展示了，在使用线性特征时，添加不同类型的合成特征时，模型的效果（区分能力）。某些情况下，使用线性特征时，不断更改参数（学习速率，不同特征的权重），仍然不能达到很好的效果，损失依旧不能到达更低的阈值。

正则化：简单行

简化正则化（Regularization for simplicity）：

  1. 当特征组合作为特征使用在模型中时，其相当于常规特征的权重，会影响最终模型的效果。
  2. 对于某些数据（比如：线性数据+噪声点），如果使用太复杂的模型（比如过多的特征组合），模型可能会与噪声拟合过度，整体性能偏低。
  3. 正则化（regularization）：降低模型的复杂度以减少过拟合。复杂度如何定量评估？之前减少过拟合是引入了验证集和测试集。
  4. 泛化曲线：表征模型泛化能力的曲线，横轴是训练迭代的次数，纵轴是损失值，可以同时画出训练集和测试集的损失。如果模型出现过拟合，可以看到训练集的损失越来越小趋于稳定，测试集的损失减小后回再增大，且远大于训练集的损失。
  5. 确保机器学习效果的要素： 1）获取正确的样本（也就是分训练集、验证集和测试集），降低训练损失； 2）正则化：不依赖于样本
  6. 正则化策略：
    • 早停法：在训练数据的效果实际收敛前停止训练。（实际操作较困难）
    • 添加惩罚项：比较常用
  7. 模型训练的目标：经验风险最小化 =》 minimize: Loss(Data|Model)
  8. 引入惩罚项，结构风险最小化 =》 minimize（Loss(Data|Model) + complexity(Model)）。减小训练误差，同时保证模型不过于复杂。
  9. 如何定义模型复杂度：首选较小的权重；偏离会产生成本
  10. 定义模型复杂度的方法：
    • 模型中所有特征的权重的函数
    • 模型中具有非零权重的特征总数的函数
  11. L2正则化（岭回归）：
    • 模型的复杂度 = 权重的平方和
    • 减少非常大的权重
    • 对于线性模型首选较平缓的斜率
    • 权重应该是以0位中心的正态分布

  12. 经过L2正则化后的损失函数： 正则化后的损失函数，包含两项：1）原始损失函数；2）惩罚项（惩罚模型的复杂度的）。其中惩罚项含有一个系数lambda，此系数可以控制（平衡）损失和惩罚的相对比例。如果有大量的数据，且训练数据和测试数据看起来比较接近，则模型很好，不需要惩罚，可设置lambda为0；如果过拟合，可以设置一定的正值，以增大整体的损失。 L2_regularization.png

  13. 执行正则化对模型的影响：
    • 使权重值接近于0，但并非为0
    • 使权重的平均值接近于0，且呈正太分布

逻辑回归

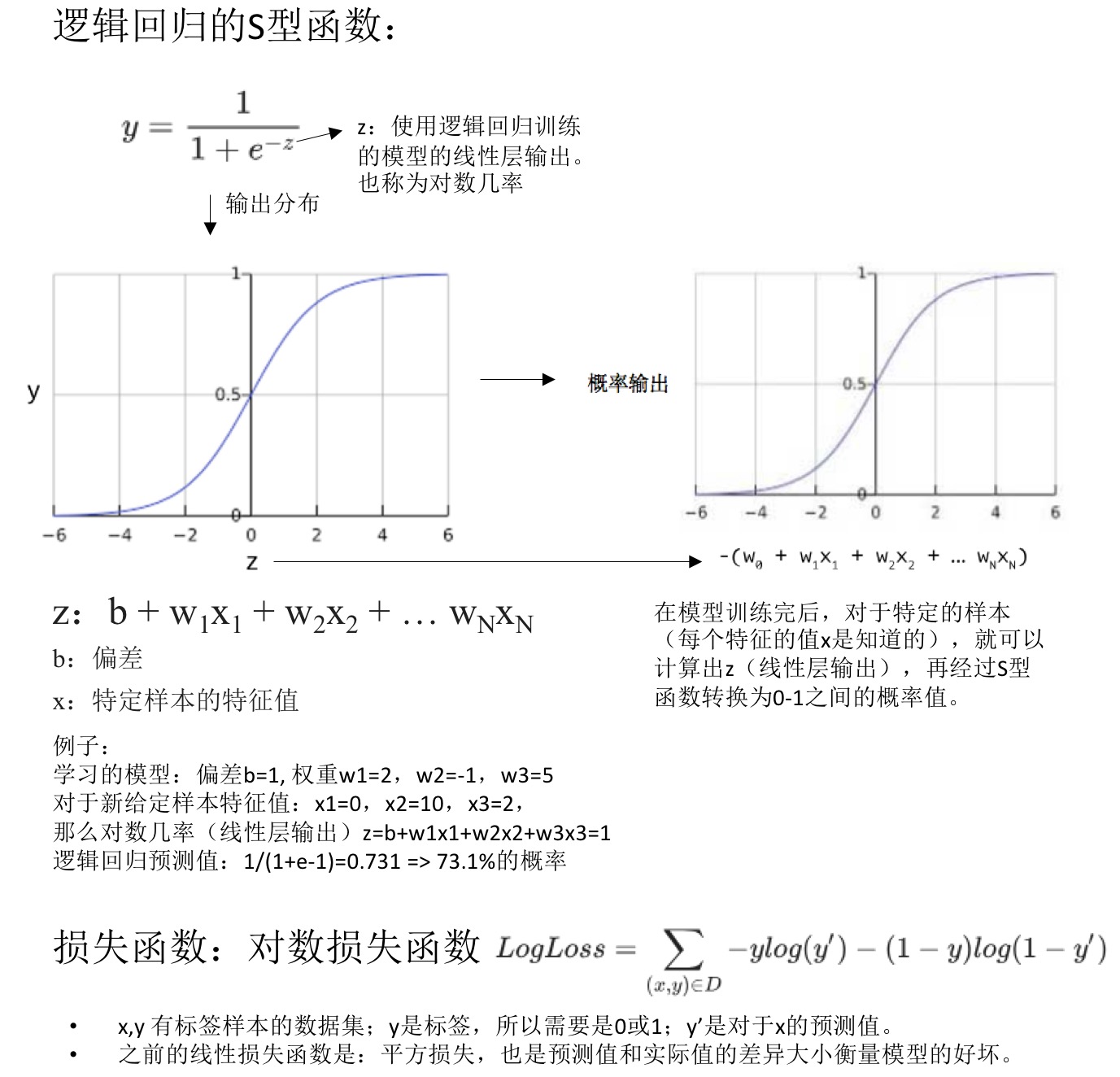
  1. 逻辑回归（logistic regression）：输出是0-1之间的概率值，不包含0和1。因为很多问题需要将概率值作为输出，而逻辑回归是一种极其高效的概率计算机制。
  2. 举例：检测垃圾邮件。模型输出为0.932，表示该电子邮件是垃圾邮件的概率为93.2%。更准确的说法：在无限训练样本下，这组样本中93.2%的是垃圾邮件，其余的6.8%不是垃圾邮件。
  3. 逻辑回归：将概率值限定在一定范围内。在某些极端的例子中，我们预测获得的结果可能是不合实际的（outliner）。
  4. 逻辑回归预测：S型函数，0-1之间的有界值。在0附近值变化很大，存在渐近线。

  5. 之前的平方损失不使用，引入对数损失函数。 logistics_regression.jpeg

  6. 正则化的重要性：
    • 记住渐近线
    • 促使损失在高维空间内达到0
  7. 逻辑回归正则化的策略：
    • L2正则化（L2权重衰减），用于降低超大权重
    • 早停法，用于限制训练步数或者学习速率
  8. 逻辑回归特点：
    • 训练速度快，预测时间短
    • 短模型、宽度模型占用大量RAM

分类

  1. 逻辑回归输出概率值，如何做分类问题？取分类阈值，高于此阈值的算作一类，低于此阈值的算作另一类（二元分类）。
  2. 评估分类模型：
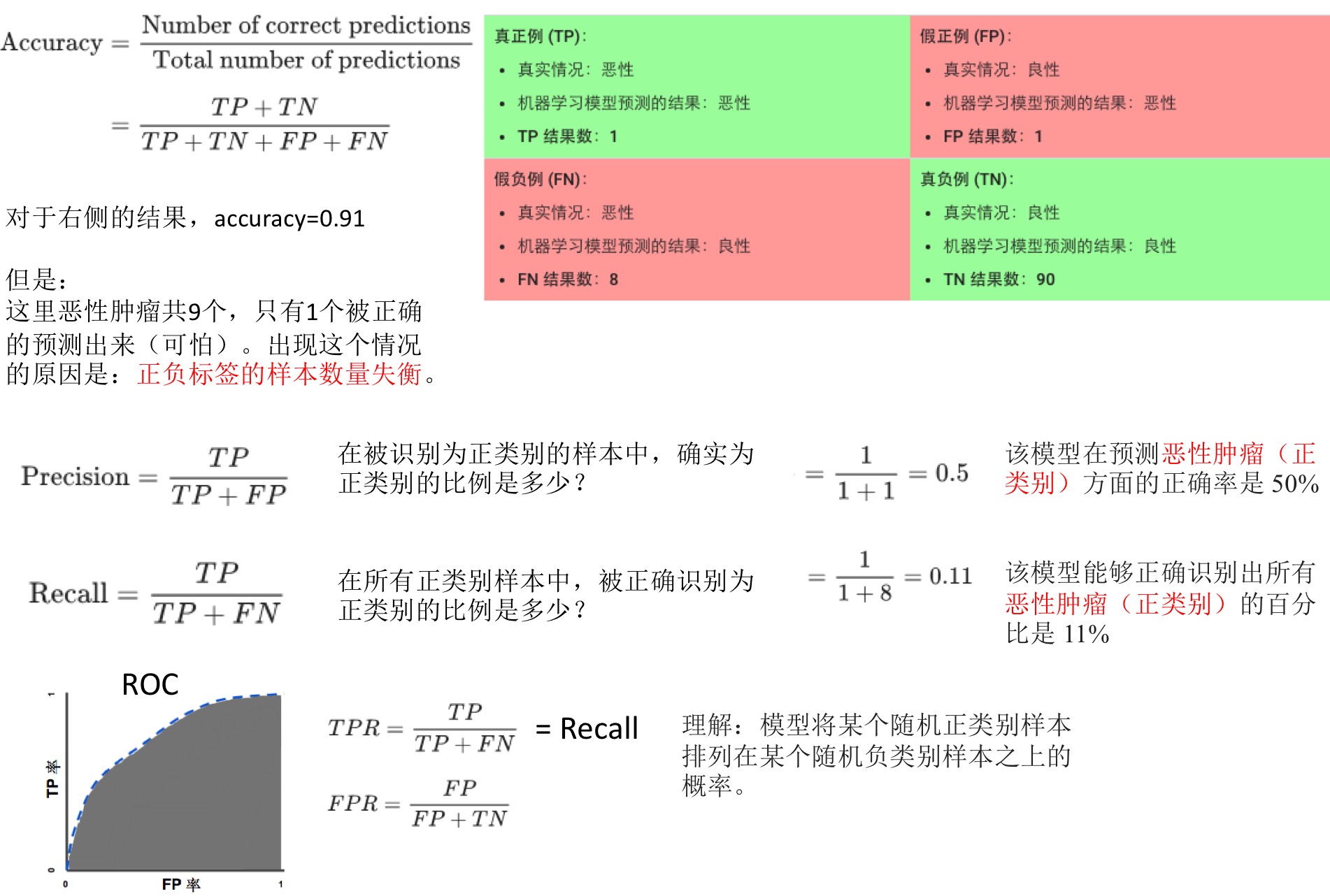
    • 准确率（accurancy）：正确的预测所占的比例（正确结果/总数）。如果类别失衡，准确率很高，但其实预测效果很差。
    • 精确率（precision）：真正例次数/所有正类别预测次数
    • 召回率（recall）：真正例次数/所有实际正类别数
    • 精确率和召回率是此消彼长的，示例通过逻辑回归获得的结果，设定不同的分类阈值时，计算精确率和召回率。当改变阈值是，两者一个变大一个减小。
    • ROC曲线：每一个点对应一个判定（分类）阈值所对应的TP率和FP率。
  3. 预测偏差：逻辑回归预测应该无偏差
    • 预测平均值 = 观察平均值
    • 零偏差 -> 并不说明系统一切完美
    • 偏差可用预测偏差曲线展示：横轴是预测值，纵轴是标签值。也可用分批策略，横轴是一批预测值的平均值，纵轴是一批观测值的平均值。 accuracy_precision_recall_ROC.jpeg
  4. 存在偏差：
    • 特征集不完整？
    • 数据集混乱？
    • 模型实现中有错误？
    • 训练样本存在偏差？（检测本身各部分数据是否存在偏差）
    • 正则化过强？
  5. 修正偏差应该在模型中，不能在校准层（添加校准层，类似于添加惩罚项？）：
    • 校准层修复的是症状，不是原因
    • 添加校准层，建立了更脆弱的系统，并且需要持续更新

正则化：稀疏性

稀疏性正则化（regularization for sparsity）

  1. 特征组合在某些时候可以增加模型的效果，但是也可能带来问题。
  2. 稀疏特征组合：
    • 大大增加特征空间。所以在高纬度稀疏矢量中，最高使其权重降至为0（不是接近于0）.
    • 导致：1）模型（RAM）变得庞大；2）噪点稀疏（从而过拟合）
  3. 当过拟合时，寻求正则化，且是特定方式的正则化：
    • 缩减模型大小
    • 降低内存使用量
    • 做法：将部分权重设为0，前面提到过的L2正则化，只能让权重变小，接近于0，不能正好为0，所以需要新的正则化方式。
  4. L0正则化：
    • 明确的将权重设为0
    • 尽可能将噪声的权重设为0，有用的特征不设为0.
    • 非凸优化；NP困难 => 所以L0不适用
  5. L1正则化（比L0更放松）：
    • 对权重之和进行惩罚
    • 凸优化问题
    • L1鼓励稀疏性，这一点和L2不同
    • 使很多信息缺乏的系数正好为0
    • 往往会减少特征的数量，从而减小模型
  6. L1 vs L2：
    • L2 -》降低 权重的平方；导数（L2）= 2*权重，每次移除权重的x%，对于任意数字，最后的值不会正好为0.
    • L1 -》降低 权重的绝对值；导数（L1）= k，每次减去一个常数。
  7. L1正则化可能使几种特征的权重为0：
    • 信息缺乏的
    • 不同程度的信息丰富的
    • 与其他类似的信息丰富特征密切相关的

神经网络简介

神经网络（Neural network）

  1. 在之前区分垃圾邮件时，可以添加特征组合（如乘积：x1x2）以提高模型效果，但是如果遇到更加复杂的数据，效果也不好
  2. 深度神经网络：复杂的非线性模型，不给定参数的学习。很好的处理复杂的数据类型，比如图片、音频、视频等
  3. 在线性模型的基础上，添加非线性模型，构成多层次的神经网络，可以构建非线性模型：
    • 一组节点。类似神经元。
    • 一组权重。与其下一层之间的关系。
    • 一组偏差，每个节点有一个偏差。
    • 一个激活函数。不同的层可能具有不同的激活函数。

neural_network.jpeg

训练神经网络

  1. 训练神经网络常用算法：反向传播算法（google提供的网页版直观说明其工作原理）。反向传播的一个概念是梯度，梯度需要是可导的，这样才能快速找到损失函数最小的地方。
  2. 反向传播算法训练失败：
    • 梯度消失。较低层梯度很小（很多小项的乘积），训练很慢甚至不再训练。ReLU激活函数有助于防止梯度消失。
    • 梯度爆炸。权重过大，很多大项的乘积，模型难以收敛。降低学习速率，有助于防止梯度爆炸。
    • ReLU单元消失。如果ReLU单元的加权和<0，岂会停滞。降低学习速率，有助于ReLU单元消失。
  3. 特征值的标准化：
    • 大致以0为中心，[-1, 1]效果比较好
    • 有助于梯度下降法收敛，避免NaN陷阱
    • 避免离群值
    • 标准化方法：1）线性缩放，2）截断（设定最大最小值），3）对数缩放。
  4. 丢弃正则化：
    • 是正则化的一种形式，对于神经网络很有用
    • 在梯度下降法的每一步随机丢弃一些网络单元，丢弃得越多，正则化效果就越强
    • 0.0 -》无丢弃
    • 1.0 -》丢弃所有（无效模型）
    • 中间值更有用

拓展参考：

多类别神经网络

  1. 多类别：multi-class neural networks
  2. 二元分类：垃圾邮件、非垃圾邮件，点击、未点击 =》逻辑回归计算类别概率
  3. 多类别问题：如区分不同的水果、颜色、动物等。最简单的想法是构建N个二元分类器，每一个分类器模型单独训练，可以判断回答单独的分类问题，最后再合并。当类别数目N较小时，是可用的，但是类别数量很大时，效率会非常低下。
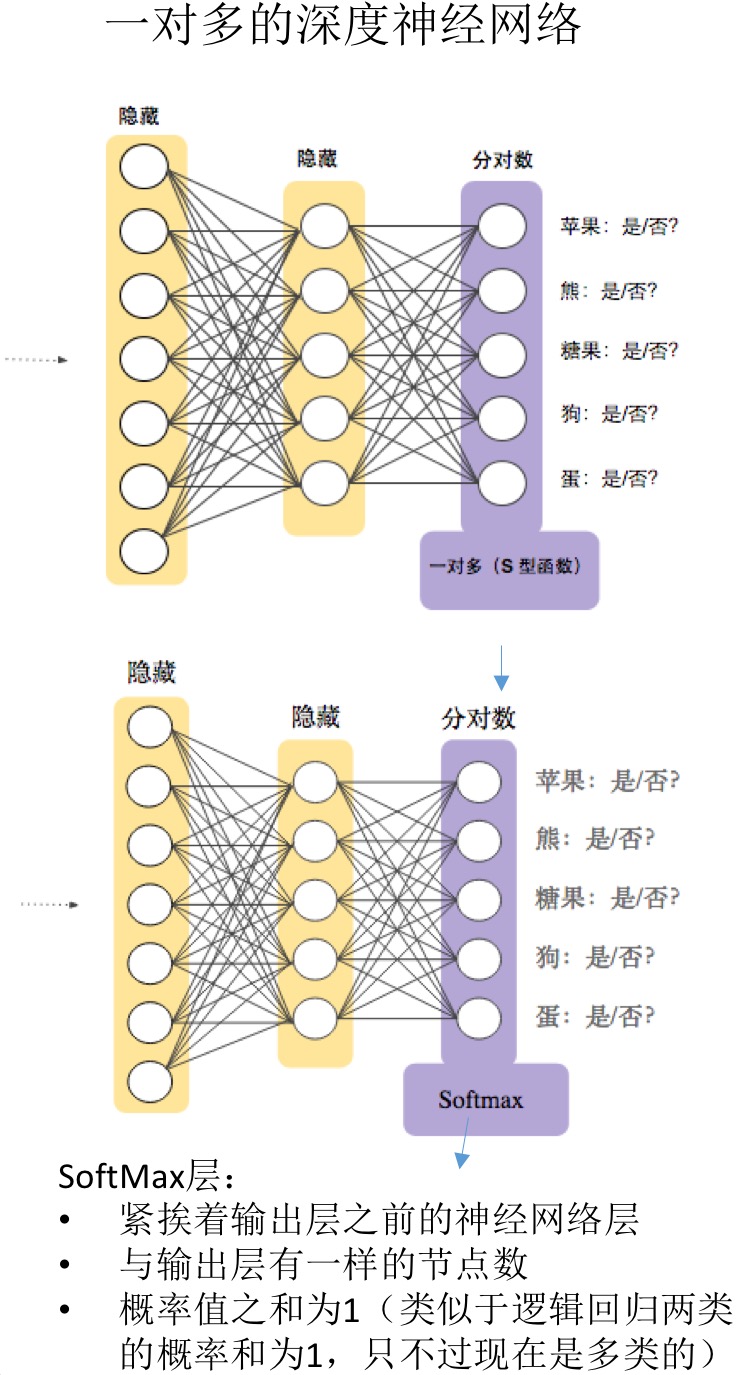
  4. 一对多多类别：对于模型的输出结果用于每个可能的类别的深度神经网络，更加的高效。
  5. 多类别单一标签：
    • 一个样本可能只是一个类别成员
    • 类别互斥
    • 一个softmax损失用于所有可能的类别
  6. 多类别多标签：
    • 一个样本可能是多个类别成员。如一个图片中可能出现了狗和香蕉
    • 无需对类别成员资格设定额外限制
    • 将一个逻辑回归损失用于每个可能的类别
  7. SoftMax：
    • 完整SoftMax：暴力破解，针对所有类别进行计算概率。
    • 候选采样：针对所有正类别标签进行计算，但负类别样本只随机选取样本进行计算。比如识别大狗和小狗，不必对每个非狗狗的样本计算概率。
    • 一个类别的成员（比如是苹果的概率）。当时多个成员时，需要用多个逻辑回归（比如是苹果、梨子的概率）。

    multiclass_neural_softmax.jpeg

嵌入

  1. 嵌套（embedding）：是一种相对低维的空间，可将高维矢量映射到这种低维空间中。所谓的嵌套，就是指用有限的特征进行描述？
  2. 推荐系统：基本点就包含嵌套。比如有一百万部电影和五十万用户，向用户推荐电影。
  3. 协同过滤（预测用户兴趣的任务）：
    • 输入：50万用户已观看的100万部影片
    • 任务：推荐电影 =》 确定哪些电影相似
  4. 整理影片（一维的）：按照相似度从左到右排列电影，一维（儿童 -》成人）。但是有的用户偏好复杂，无法准确推荐。
  5. 整理影片（二维的）：一维（儿童 -》成人），二维（艺术类 -》卖座的）。可以看到相似的电影在二维中更加靠近。
  6. 二维嵌套：上面的二维整理在坐标轴中，每个电影（点）可用两个值来描述，这些电影（点）之间的距离就是他们的相似性。
  7. d维嵌套：每个样本通过d个方面分析，变成一个d维的点。
  8. 在深度神经网络中学习嵌套：
    • 无需单独训练
    • 监督式信息（两个用户观看了同一电影）
  9. 输入表示法（协同过滤，用户影片观看与否的矩阵）：
    • 样本就是一个一维的稀疏矩阵，表示电影的观看与否。数量庞大，表示法低效。
    • 字典表示，key是用户，value是看过的电影的编号。稀疏张量是分类数据的一种高效表示方法，但是对于大数据集不适用。
  10. 例子：
    • 房屋售价的回归问题
    • 预测手写字的多类别分类
    • 推荐影片。如果构建lable，可以对每个用户，挑7部作为训练集合，那么剩下的就是目标答案了。
  11. 嵌套维度个数：
    • 越多，越能准确的表示输入值之间的关系
    • 越多，训练会越慢，过拟合的可能性也越高
    • dimension -> 所有可能值个数的开四次方
  12. 标准降维技术：PCA -》查找高度相关且可以合并的维度

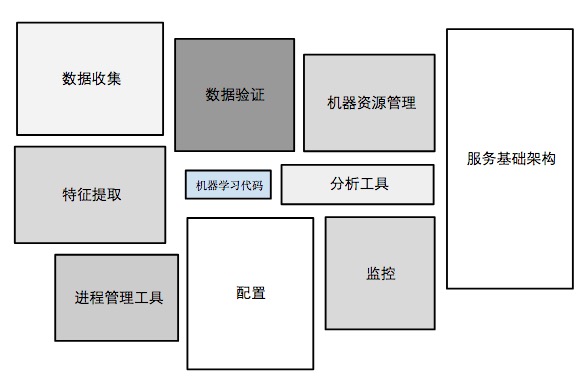
机器学习工程

生产环境机器学习系统

MlSystem.jpeg

静态训练与动态训练

  1. 静态训练（static）：
    • 离线式
    • 只训练模型一次，然后使用模型
    • 易于构建和测试
    • 适用于数据集不随时间而改变的
    • 需要监控输入数据是否发生变化
  2. 动态训练（dynamic）：
    • 在线式
    • 数据会不断进入系统，更新模型以整合这些数据
    • 例子：预测买花行为，如果只用7、8月的数据，那么预测情人节前后的效果很差

静态推理与动态推理

  1. 静态推理：
    • 记录预测并缓存供查询
    • 不需担心推理成本
    • 可使用批量方法或巨型MapReduce方法
    • 可在推送前对预测进行后期验证
    • 只能对我们知晓的数据进行预测，不适用存在长尾的情况
    • 更新可能延迟数小时或数天
  2. 动态推理：
    • 使用服务器根据需要进行预测
    • 可在新项目加入时预测，适合存在长尾的情况
    • 计算量大，对延迟敏感，会限制模型的复杂度
    • 监控需求更多

数据依赖关系

  1. 输入数据的特征和品质对于模型很重要
  2. 数据可靠性：
    • 信号是否始终可用？
  3. 版本控制：
    • 计算此数据的系统是否发生过变化？多久一次？
  4. 必要性：
    • 添加新的特征或样本，是否能很大程度提高模型的准确性
  5. 反馈环：
    • 是否依赖于其他模型，如果其他模型出错怎么办？

机器学习现实世界应用示例

癌症预测

  1. 目标：根据病人的一些特征预测是否患有癌症
  2. 特征：年龄、性别、病史、医院名称、生命特征、检验结果
  3. 结果：在训练和测试数据上表现良好，在新的预测数据上表现糟糕
  4. 原因：”医院名称“作为一个特征，这个跟是否真实的患有癌症没有关系，名称包含癌症可能病人不含有癌症，名称不包含癌症可能病人是含有癌症的。

18世纪文学

  1. 目标：根据隐喻语句预测作者的政治派别
  2. 特征：没说，可能包含很多，词频，作者信息等
  3. 结果：在测试数据上表现完美
  4. 原因：数据集的拆分出现猫腻。对于每个作者，其某些句子作为训练集，某些作为验证集，某些作为测试集。这样一来，模型学习了不止隐喻的特征，也学习了作者的额外信息，从而使的效果很好（但并不是隐喻带来的效果）。

现实世界应用准则

有效的机器学习准则：

  • 确保第一个模型简单易用
  • 着重确保数据的正确性
  • 使用简单可观察的指标进行训练和评估
  • 特征输入并监控
  • 代码化模型
  • 记录所有实验结果，包括失败的，方便优化和调试

总结

  1. 后续步骤

If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/google-machine-learning.html
Previous: 100 pandas puzzles

    Category

    Latest articles

    Links