- 预热
- 问题构建
- 深入了解机器学习
- 降低损失
- 使用TensorFlow的起始步骤
- 训练集和测试集
- 验证
- 表示法
- 特征组合
- 简化正则化
- 分类
- 稀疏正则化
- 神经网络简介
- 训练神经网络
- 多类别神经网络
- 嵌套
- 静态训练和动态训练
- 静态推理和动态推理
- 数据依赖关系
谷歌机器学习课程对应的练习。
预热
- Hello World: 正常导入TF模块,其提供的notebook都是基于python3的,所以最好安装anaconda3,然后安装对应的tensorflow。
- TensorFlow编程概念:
- 张量(tensors):任意维度的数组。可作为常量或变量存储在图中。
- 标量:零维数组(零阶张量);矢量:一维数组(一阶张量);矩阵:二维数组(二阶张量)
- 指令:创建、销毁和操控张量
- 图(计算图、数据流图):图数据结构,其节点是指令,边是张量。
- 会话
- 1)将常量、变量和指令整合到一个图中;2)在一个会话中评估这些常量、变量和指令。
- 创建和操控张量:
- 矢量加法:类似于python里面的数组(numpy数组),比如元素级加法、元素翻倍等。 函数:
tf.add(x,y) - 广播:元素级运算中的较小数组会增大到与较大数组具有相同的形状。一般数学上只支持形状相同的张量进行元素级的运算,但是TF中借鉴Numpy的广播做法。
twos = tf.constant([2, 2, 2, 2, 2, 2], dtype=tf.int32)
primes_doubled = primes * twos
print("primes_doubled:", primes_doubled)
# 输出值包含值和形状(shape)、类型信息
primes_doubled: tf.Tensor([ 4 6 10 14 22 26], shape=(6,), dtype=int32)
- 矩阵乘法:第一个举证的列数必须等于第二个矩阵的行数。函数:
tf.matmul - 张量变形:矩阵运算限制了矩阵的形状,因此需要频繁变化,可调用
tf.reshape函数,改变形状或者阶数。 - 变量初始化和赋值:如果定义的是变量,需要进行初始化,这个值之后是可以更改(函数:
tf.assign)的。
v = tf.contrib.eager.Variable([3])
print(v)
tf.assign(v, [7])
print(v)
[3]
[7]
模拟投两个骰子10次,10x3的张量,第三列是前两列的和:
random_uniform:随机选取tf.concat:合并张量
die1 = tf.contrib.eager.Variable(
tf.random_uniform([10, 1], minval=1, maxval=7, dtype=tf.int32))
die2 = tf.contrib.eager.Variable(
tf.random_uniform([10, 1], minval=1, maxval=7, dtype=tf.int32))
dice_sum = tf.add(die1, die2)
resulting_matrix = (values=[die1, die2, dice_sum], axis=1)
print(resulting_matrix.numpy())
[[5 1 6]
[4 5 9]
[1 6 7]
[2 3 5]
[1 2 3]
[5 4 9]
[3 5 8]
[3 2 5]
[3 1 4]
[6 3 9]]
- Pandas简介:
- DataFrame:数据表格
- Series:单一列
- 利用索引随机化数据
- 重建索引不包含时,会添加新行,并以
NaN填充
cities
City name Population Area square miles Population density
0 San Francisco 852469 46.87 18187.945381
1 San Jose 1015785 176.53 5754.177760
2 Sacramento 485199 97.92 4955.055147
# 随机化index,然后重建索引
cities.reindex(np.random.permutation(cities.index))
# 索引超出范围不报错,新建行
cities.reindex([0, 4, 5, 2])
问题构建
- 【监督式学习】:假设您想开发一种监督式机器学习模型来预测指定的电子邮件是“垃圾邮件”还是“非垃圾邮件”。以下哪些表述正确?
有些标签可能不可靠。未标记为“垃圾邮件”或“非垃圾邮件”的电子邮件是无标签样本。- 我们将使用无标签样本来训练模型。
- 主题标头中的字词适合做标签。
- 【特征和标签】:假设一家在线鞋店希望创建一种监督式机器学习模型,以便为用户提供合乎个人需求的鞋子推荐。也就是说,该模型会向小马推荐某些鞋子,而向小美推荐另外一些鞋子。以下哪些表述正确?
- 鞋的美观程度是一项实用特征。
- 用户喜欢的鞋子是一种实用标签。
“用户点击鞋子描述”是一项实用标签。鞋码是一项实用特征。
深入了解机器学习
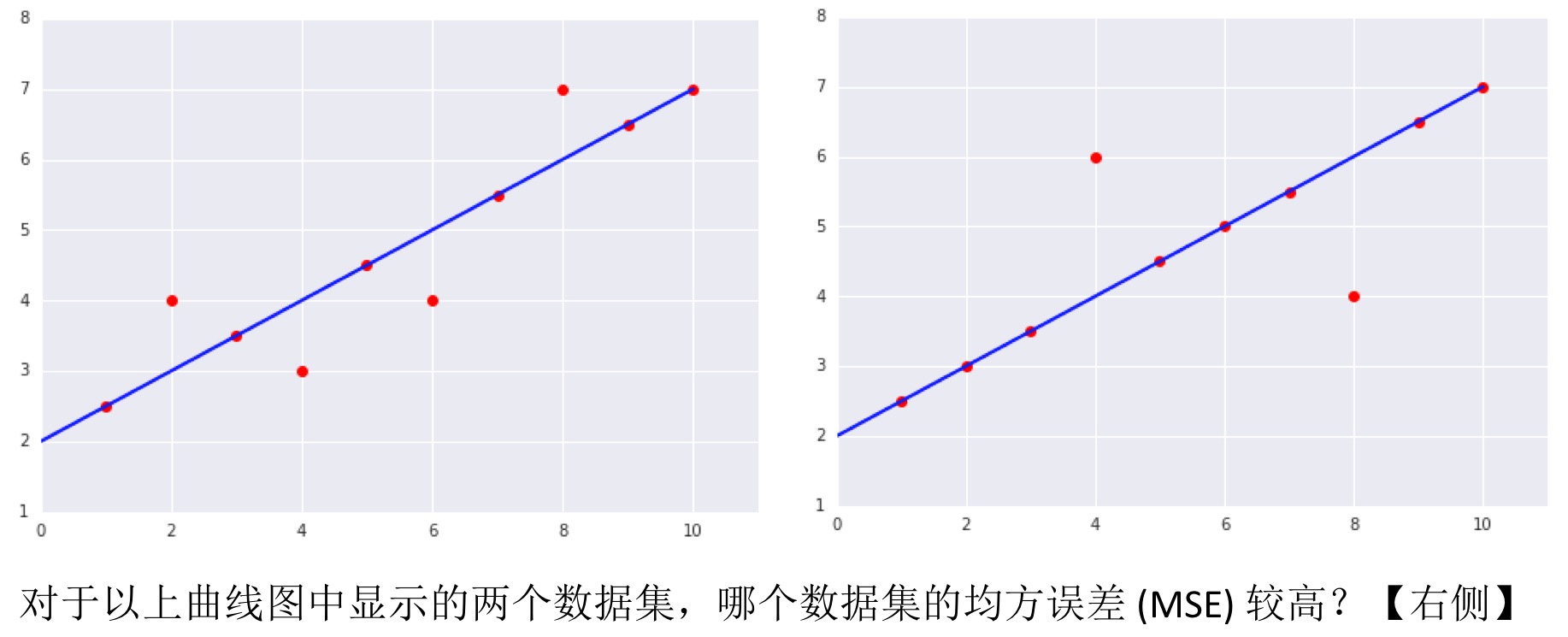
均方误差:
降低损失
- 优化学习速率:
- Learning rate is a hyper-parameter that controls how much we are adjusting the weights of our network with respect the loss gradient(ref). 所以需要不断的更新权重值,看更新后的损失值是否变小,所以横轴是权重,纵轴是损失值。
- 新权重 = 旧权重 — 学习速率 * 梯度
- 在训练模型时,需要最小化损失函数,通常沿着梯度下降的方向。能否找到、多久找到损失函数的最小值,需要进行尝试,一个重要的参数就是学习速率(learning rate)。
学习速率*梯度就是每次更新的数值。 - 这个页面以互动的方式,调节学习速率,看损失函数(二项函数)经过多少步能到达最小损失处。
- 这个图也展示了不同的学习速率可能导致的结果:太小则收敛太慢,太大则很难找到最小值处:

- 【批量大小】:基于大型数据集执行梯度下降法时,以下哪个批量大小可能比较高效?
小批量或甚至包含一个样本的批量 (SGD)。- 全批量。
- 学习速率和收敛: 学习速率越小,收敛所花费的时间越多。在这个练习中,可以尝试不同的学习速率,看能否收敛以及收敛所需的迭代次数。
使用TensorFlow的起始步骤
任务:基于单个输入特征预测各城市街区的房屋价值中位数
# 准备feature和target数据,这里只用一个特征
my_feature = california_housing_dataframe[["total_rooms"]]
feature_columns = [tf.feature_column.numeric_column("total_rooms")]
targets = california_housing_dataframe["median_house_value"]
# 配置训练时的优化器
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0000001)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
# 配置模型
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=feature_columns,
optimizer=my_optimizer
)
def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
"""Trains a linear regression model of one feature.
"""
features = {key:np.array(value) for key,value in dict(features).items()}
ds = Dataset.from_tensor_slices((features,targets)) # warning: 2GB limit
ds = ds.batch(batch_size).repeat(num_epochs)
if shuffle:
ds = ds.shuffle(buffer_size=10000)
# Return the next batch of data.
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
# 训练模型
_ = linear_regressor.train(
input_fn = lambda:my_input_fn(my_feature, targets),
steps=100
)
# 评估模型
prediction_input_fn =lambda: my_input_fn(my_feature, targets, num_epochs=1, shuffle=False)
predictions = linear_regressor.predict(input_fn=prediction_input_fn)
predictions = np.array([item['predictions'][0] for item in predictions])
mean_squared_error = metrics.mean_squared_error(predictions, targets)
root_mean_squared_error = math.sqrt(mean_squared_error)
print("Mean Squared Error (on training data): %0.3f" % mean_squared_error)
print("Root Mean Squared Error (on training data): %0.3f" % root_mean_squared_error)
Mean Squared Error (on training data): 56367.025
Root Mean Squared Error (on training data): 237.417
模型效果好吗?通过RMSE(特性:它可以在与原目标相同的规模下解读),直接与原来target的最大最小值,进行比较。在这里,误差跨越了目标范围的一半,所以需要优化模型减小误差。
Min. Median House Value: 14.999
Max. Median House Value: 500.001
Difference between Min. and Max.: 485.002
Root Mean Squared Error: 237.417
问题:有适用于模型调整的标准启发法吗?
- 不同超参数的效果取决于数据,不存在必须遵循的规则,需要自行测试和验证。
- 好的模型应该看到训练误差应该稳步减小(刚开始是急剧减小),最终收敛达到平衡。
- 如果训练误差减小速度过慢,则提高学习速率也许有助于加快其减小速度。
- 如果训练误差变化很大,尝试降低学习速率。
- 较低的学习速率和较大的步数/较大的批量大小通常是不错的组合。
- 批量大小过小也会导致不稳定情况。不妨先尝试 100 或 1000 等较大的值,然后逐渐减小值的大小,直到出现性能降低的情况。
- 合成特征和离群值:
- 比如预测平均房价时把
total_rooms/population作为一个特征,表示的是平均每个人有多少个房间,这个是可取的。 - 识别离群值:
- 1)画target和prediction的散点图,看是否在一条直线上
- 2)画训练所用特征数据的分布图,看是否存在极端值
- 截取离群值:设上下限值,超过的设置为对应的值
clipped_feature = df["feature_name"].apply(lambda x: max(x, 0)),再重新训练,看是否效果变好了。
- 比如预测平均房价时把
训练集和测试集
训练集和测试集:调整训练集和测试集的相对比例,查看模型的效果。不同的数据集需要不同的比例,这个得通过尝试才能确定。
如何确定各data set之间的比例,没有统一的标准,取决于不同的条件 About Train, Validation and Test Sets in Machine Learning:
- 取决于样本数量。
- 取决于所训练的模型。比如参数很多,可能需要很多数据进行验证。
验证
- 检验您的直觉:验证: 我们介绍了使用测试集和训练集来推动模型开发迭代的流程。在每次迭代时,我们都会对训练数据进行训练并评估测试数据,并以基于测试数据的评估结果为指导来选择和更改各种模型超参数,例如学习速率和特征。这种方法是否存在问题?
多次重复执行该流程可能导致我们不知不觉地拟合我们的特定测试集的特性。- 完全没问题。我们对训练数据进行训练,并对单独的预留测试数据进行评估。
- 这种方法的计算效率不高。我们应该只选择一个默认的超参数集,并持续使用以节省资源。
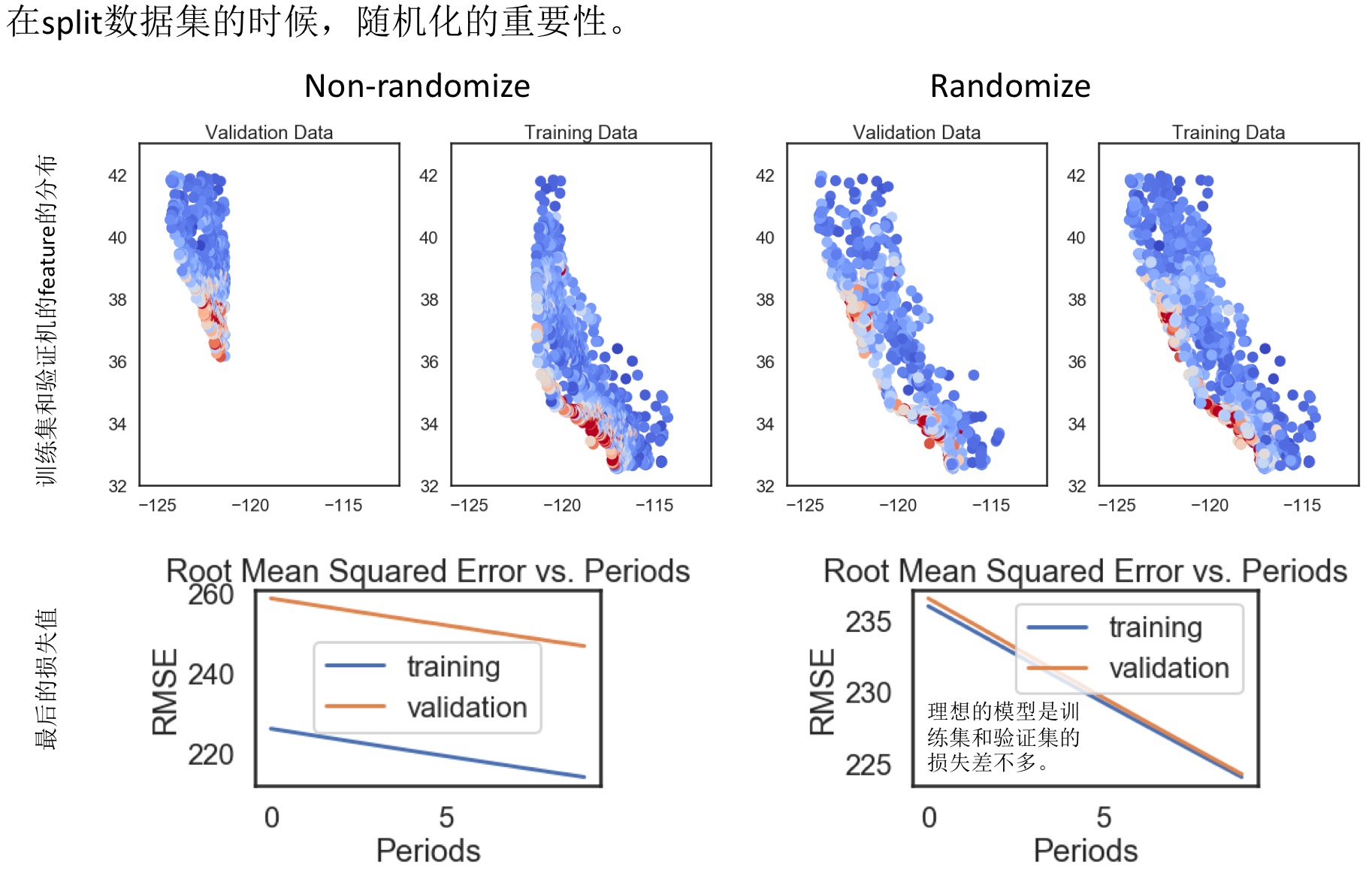
- 拆分验证集:
表示法
- 特征集:
- 相关矩阵(Pearson coefficient):探索不同特征之间的相似性
- 更好的利用纬度信息:直观的纬度与房价没有线性关系,但是有的峰值可能与特定地区有关 =》可以把纬度转换为这些特定地区的相对值。
特征组合
- Feature Crosses练习: 对于线性不可分的问题,有时根据管擦的规律添加新的组合特征,可能解决问题,一个很经典的例子如下:
- Feature Crosses理解:加利福尼亚州不同城市的房价有很大差异。假设您必须创建一个模型来预测房价。以下哪组特征或特征组合可以反映出特定城市中 roomsPerPerson 与房价之间的关系?
- 两个特征组合:[binned latitude X binned roomsPerPerson] 和 [binned longitude X binned roomsPerPerson]
一个特征组合:[binned latitude X binned longitude X binned roomsPerPerson]- 一个特征组合:[latitude X longitude X roomsPerPerson]
- 三个独立的分箱特征:[binned latitude]、[binned longitude]、[binned roomsPerPerson]
- Feature Crosses编程:
- 离散特征的独热编码:即在训练逻辑回归模型之前,离散(即字符串、枚举、整数)特征会转换为二元特征系列。
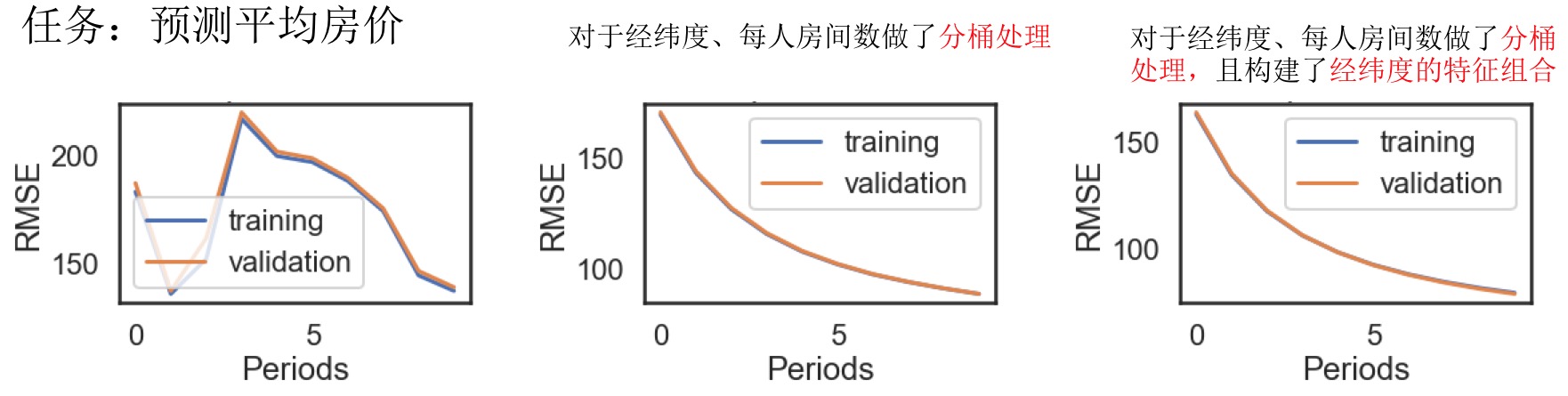
- 分桶(分箱)特征:函数
bucketized_column,转换为对应的类别编码,然后再进行独热编码(成二元特征系列)。 - 特征组合及分桶处理特征有时能大幅度提升模型的效果。
- 特征分桶函数:
bucketized_longitude = tf.feature_column.bucketized_column( longitude, boundaries=get_quantile_based_boundaries( training_examples["longitude"], 10)) - 特征组合函数:
long_x_lat = tf.feature_column.crossed_column( set([bucketized_longitude, bucketized_latitude]), hash_bucket_size=1000)
简化正则化
- 简化正则化练习:对于某些问题,可能因为使用过多的特征或者特征组合,使得模型训练很好,但是泛化能力很低。通常模型的过拟合包含多方面的原因,比如:1)模型太复杂;2)数据量太少;3)使用的特征太多。
- 简化正则化理解:
- 【L2正则化】:假设某个线性模型具有100个输入特征,其中10个特征信息丰富,另外90个特征信息比较缺乏,假设所有特征的值均介于 -1 和 1 之间。 以下哪些陈述属实?
L2 正则化可能会导致对于某些信息缺乏的特征,模型会学到适中的权重。L2 正则化会使很多信息缺乏的权重接近于(但并非正好是)0.0。- L2 正则化会使大多数信息缺乏的权重正好为 0.0。
- 【L2 正则化和相关特征】:假设某个线性模型具有两个密切相关的特征;也就是说,这两个特征几乎是彼此的副本,但其中一个特征包含少量的随机噪点。如果我们使用 L2 正则化训练该模型,这两个特征的权重将出现什么情况?
- 其中一个特征的权重较大,另一个特征的权重几乎为 0.0。
- 其中一个特征的权重较大,另一个特征的权重正好为 0.0。
这两个特征将拥有几乎相同的适中权重。
- 【L2正则化】:假设某个线性模型具有100个输入特征,其中10个特征信息丰富,另外90个特征信息比较缺乏,假设所有特征的值均介于 -1 和 1 之间。 以下哪些陈述属实?
分类
- 【准确率】:在以下哪种情况下,高的准确率值表示机器学习模型表现出色?
在 roulette 游戏中,一只球会落在旋转轮上,并且最终落入 38 个槽的其中一个内。某个机器学习模型可以使用视觉特征(球的旋转方式、球落下时旋转轮所在的位置、球在旋转轮上方的高度)预测球会落入哪个槽中,准确率为 4%。- 一种致命但可治愈的疾病影响着 0.01% 的人群。某个机器学习模型使用其症状作为特征,预测这种疾病的准确率为 99.99%。
- 一只造价昂贵的机器鸡每天要穿过一条交通繁忙的道路一千次。某个机器学习模型评估交通模式,预测这只鸡何时可以安全穿过街道,准确率为 99.99%。
- 【精确率】:让我们以一种将电子邮件分为“垃圾邮件”或“非垃圾邮件”这两种类别的分类模型为例。如果提高分类阈值,精确率会怎样?
可能会提高。- 一定会提高。
- 可能会降低。
- 一定会降低。
- 【召回率】让我们以一种将电子邮件分为“垃圾邮件”或“非垃圾邮件”这两种类别的分类模型为例。如果提高分类阈值,召回率会怎样?
始终下降或保持不变。- 始终保持不变。
- 一定会提高。
- 【精确率和召回率】以两个模型(A 和 B)为例,这两个模型分别对同一数据集进行评估。 以下哪一项陈述属实?
- 如果模型 A 的精确率优于模型 B,则模型 A 更好。
- 如果模型 A 的召回率优于模型 B,则模型 A 更好。
如果模型 A 的精确率和召回率均优于模型 B,则模型 A 可能更好。
- 理解ROC和AUC:
- 【ROC和AUC】:以下哪条 ROC 曲线可产生大于 0.5 的 AUC 值?
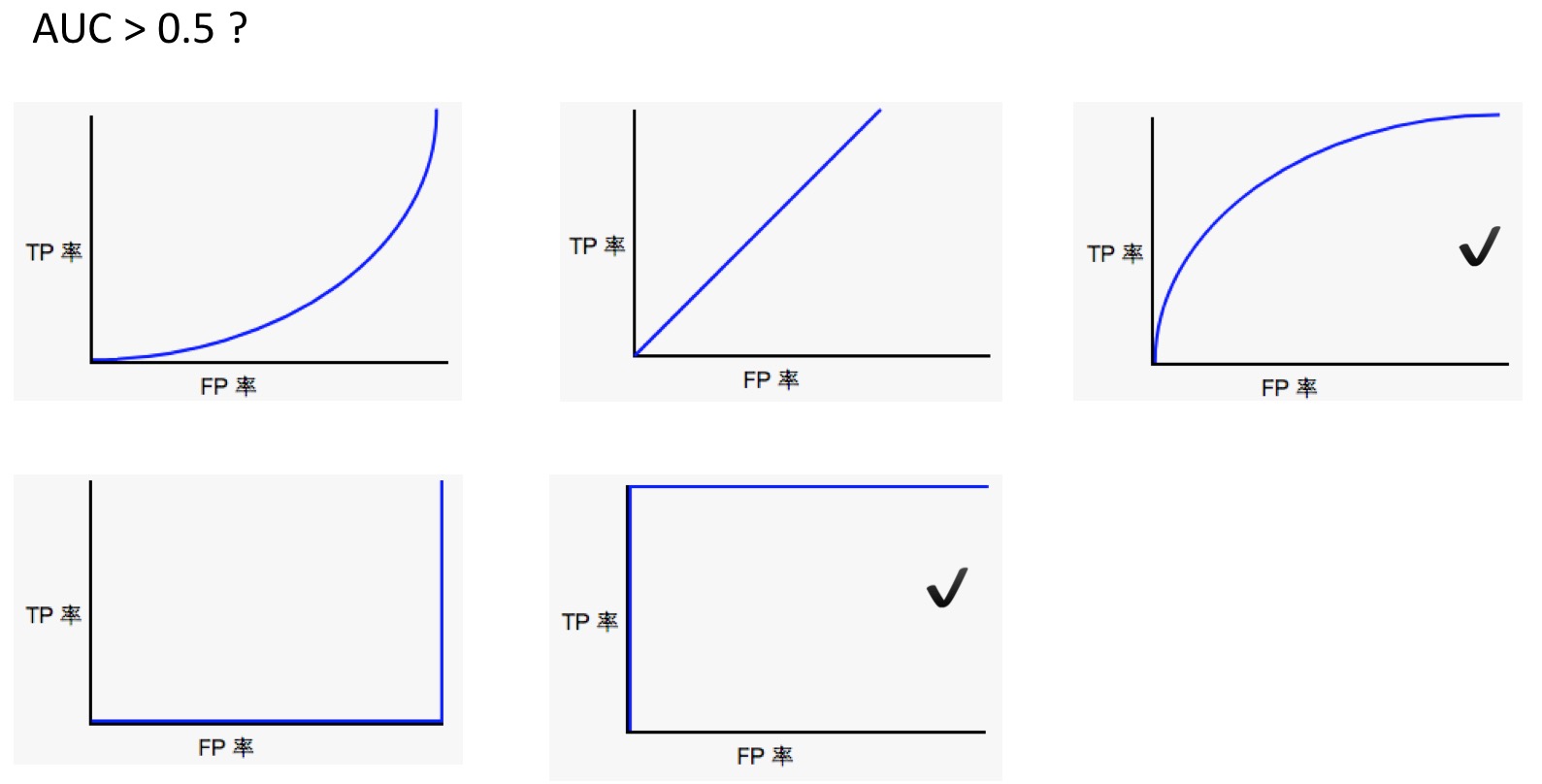
- 【AUC 和预测结果的尺度】:将给定模型的所有预测结果都乘以 2.0(例如,如果模型预测的结果为 0.4,我们将其乘以 2.0 得到 0.8),会使按 AUC 衡量的模型效果产生何种变化?
- 这会使 AUC 变得很糟糕,因为预测值现在相差太大。
- 这会使 AUC 变得更好,因为预测值之间相差都很大。
没有变化。AUC 只关注相对预测分数。
稀疏正则化
【L1正则化】:假设某个线性模型具有100个输入特征,其中10个特征信息丰富,另外90个特征信息比较缺乏。假设所有特征的值均介于-1和1之间。以下哪些陈述属实?
L1 正则化可能会使信息丰富的特征的权重正好为 0.0。- L1 正则化会使很多信息缺乏的权重接近于(但并非正好是)0.0。
L1 正则化会使大多数信息缺乏的权重正好为 0.0。
【L1和L2正则化】:假设某个线性模型具有 100 个输入特征,这些特征的值均介于-1到1之间,其中10个特征信息丰富,另外90个特征信息比较缺乏。哪种类型的正则化会产生较小的模型?
L1 正则化。- L2 正则化。
- 编程练习:
- 将房屋价格的预测变换为一个分类问题:预测房价是否过高
- 对于房价,取75%阈值,最高的75%认为是过高的(可设为1),其他的是不过高的(可设为0)
- 比较线性模型和逻辑回归模型用于房屋。注意这里两者的损失函数是不同的,不能直接比较所画的损失函数曲线的纵轴,可以在线性模型中计算对数损失,从而比较两个模型。
- 一般提高模型的效果,可以训练更长的时间,可以增加步数和/或批量大小。
- 在调整参数优化模型的时候,最好在集群上调试。对于此练习的最后一个优化,在iMAC上跑挂了,电脑差点不能正常启动。
神经网络简介
-
神经网络:在线性很难区分的数据集上,测试不同的神经网络结构(隐藏层、权重、激活函数等),查看效果。
-
构建神经网络: 函数
hidden_units,例子hidden_units=[3, 10]表示指定了连个隐藏层,第一个隐藏层含有3个节点,第二个隐藏层含有10个节点,默认为全连接且使用ReLU激活函数。 -
编程联系:时间问题,神经网络的训练需要大量的时间和运算,所以最好在集群上进行,不要在本地电脑上。
# Create a DNNRegressor object.
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
dnn_regressor = tf.estimator.DNNRegressor(
feature_columns=construct_feature_columns(training_examples),
hidden_units=hidden_units,
optimizer=my_optimizer
)
# Create input functions.
training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
batch_size=batch_size)
predict_training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
num_epochs=1,
shuffle=False)
predict_validation_input_fn = lambda: my_input_fn(validation_examples,
validation_targets["median_house_value"],
num_epochs=1,
shuffle=False)
训练神经网络
- 线性缩放:将输入缩放到(-1, 1)之间,SGD在不同维度中改变步长不受阻。
def linear_scale(series):
min_val = series.min()
max_val = series.max()
scale = (max_val - min_val) / 2.0
return series.apply(lambda x:((x - min_val) / scale) - 1.0)
- 尝试不同的优化器:Adam适合非凸优化问题,AdaGrad适合凸优化问题。
- 尝试其他的标准化方法:
def log_normalize(series):
return series.apply(lambda x:math.log(x+1.0))
def clip(series, clip_to_min, clip_to_max):
return series.apply(lambda x:(
min(max(x, clip_to_min), clip_to_max)))
def z_score_normalize(series):
mean = series.mean()
std_dv = series.std()
return series.apply(lambda x:(x - mean) / std_dv)
def binary_threshold(series, threshold):
return series.apply(lambda x:(1 if x > threshold else 0))
- 仅适用部分特征,这里也涉及到特征挑选?对于模型效果的提升能有多大的作用?
多类别神经网络
- 训练线性模型和神经网络,对MNIST数据集的手写数字进行分类
- 比较线性分类模型和神经网络模型的效果
- 可视化神经网络隐藏层的权重
嵌套
- 将影评字符串数据转换为稀疏特征矢量
- 使用稀疏特征矢量实现情感分析线性模型
- 通过将数据投射到二维空间的嵌入来实现情感分析 DNN 模型
- 将嵌入可视化,以便查看模型学到的词语之间的关系
静态训练和动态训练
【在线训练】:以下哪个关于在线(动态)训练的表述是正确的?
- 几乎不需要对训练作业进行监控。
- 在推理时几乎不需要监控输入数据。
模型会在新数据出现时进行更新。
【离线训练】:以下哪些关于离线训练的表述是正确的?
- 模型会在收到新数据时进行更新。
与在线训练相比,离线训练需要对训练作业进行的监控较少。- 在推理时几乎不需要监控输入数据。
您可以先验证模型,然后再将其应用到生产中。
静态推理和动态推理
【在线推理】:在线推理指的是根据需要作出预测。也就是说,进行在线推理时,我们将训练后的模型放到服务器上,并根据需要发出推理请求。以下哪些关于在线推理的表述是正确的?
您可以为所有可能的条目提供预测。- 在进行在线推理时,您不需要像执行离线推理一样,过多地担心预测延迟问题(返回预测的延迟时间)。
您必须小心监控输入信号。- 您可以先对预测进行后期验证,然后再使用它们。
【离线推理】:在离线推理中,我们会一次性根据大批量数据做出预测。然后将这些预测纳入查询表中,以供以后使用。以下哪些关于离线推理的表述是正确的?
对于给定的输入,离线推理能够比在线推理更快地提供预测。生成预测之后,我们可以先对预测进行验证,然后再应用。- 我们会对所有可能的输入提供预测。
- 我们将需要在长时间内小心监控输入信号。
- 我们将能够快速对世界上的变化作出响应。
数据依赖关系
Data Dependencies理解:以下哪个模型容易受到反馈环的影响?
大学排名模型 - 将选择率(即申请某所学校并被录取的学生所占百分比)作为一项学校评分依据。图书推荐模型 - 根据小说的受欢迎程度(即图书的购买量)向用户推荐其可能喜欢的小说。交通状况预测模型 - 使用海滩上的人群规模作为特征之一预测海滩附近各个高速公路出口的拥堵情况。- 选举结果预测模型 - 在投票结束后对 2% 的投票者进行问卷调查,以预测市长竞选的获胜者。
- 住宅价值预测模型 - 使用建筑面积(以平方米为单位计算的面积)、卧室数量和地理位置作为特征预测房价。
- 人脸检测模型:检测照片中的人是否在微笑(根据每月自动更新的照片数据库定期进行训练)。
If you link this blog, please refer to this page, thanks!
Post link:https://tsinghua-gongjing.github.io/posts/google_ML_excercises.html
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me