目录

• 目录
• 随机森林：bagging
• 自适应上升决策树（adaptive boosted decision tree）：Adaboost
  • 通过带权重的采样引入权重
  • 采用弱的决策树
  • 高度为1时就是AdaBoost-Stump(切割)
  • 目标优化函数及求解
  • 二分类扩展到普遍
  • sklearn调用AdaBoost
• 梯度上升决策树
  • sklearn调用GBDT
• aggregation模型总结
  • 5种aggregation方法
  • blending（混合）：单个模型已知
  • learning：单个模型未知
  • learning中的aggregate模型的再组合
  • aggregation优点
• 参考

随机森林：bagging

• 随机森林：通过boostrap从原样本D随机选取得到新样本D‘，对每个D’训练得到不同的模型\(g_t\)，最后通过uniform（投票）形式组合起成G。
• uniform：bagging方式

自适应上升决策树（adaptive boosted decision tree）：Adaboost

• 【AdaBoost-D Tree】如果将随机森林中的bagging换为AdaBoost：每轮bootstrap得到的D‘中每个样本会赋予不同的权重\(u^{(t)}\)，然后每个决策树中，利用权重得到对应的最好模型\(g_t\)，最后得出每个\(g_t\)所占的权重，线性组合得到G。
• Adaptive Boosting的bootstrap操作：有放回的抽样，\(u^{(t)}\)表示每个样本在D’中出现的次数。

通过带权重的采样引入权重

• 决策树CART中没有引入\(u^{(t)}\)，如果把权重引入进来？
• 采用weighted算法：\(E_{in}^{u}(h)=\frac{1}{N}\sum_{n-1}^N * err(y_n, h(x_n))\)，即：每个犯错的样本点乘以权重，求和取平均

• 同理：对决策树的每个分支进行如此计算。复杂不易求解！！！

• 权重\(u^{(t)}\)：该样本在bootstrap中出现的次数（概率）
• 根据u值，对原样本进行一次重新的带权重的随机抽样（sampling），得到的新D‘每个样本出现的几率与其权重是近似的。
• 因此使用带权重的随机抽样得到的数据，直接进行决策树训练，从而无需改变决策树结构。
• sampling可认为是bootstrap的反操作
• AdaBoost-DTree：AdaBoost+sampling+DTree
• 每个训练的\(g_t\)权重：计算其错误率，转换为权重

采用弱的决策树

• 问题：
  • 完全长成的树（fully grown tree）：
  • 所有样本x训练而成
  • 如果每个样本均不同，错误率为0，权重为无限大（其他模型没有效果）。
  • 这就是autocracy（专制的），不是我们想要的结果
  • 希望通过把不同的\(g_t\) aggregation起来，发挥集体智慧。
  • 专制的原因：【1】使用了所有样本进行训练，【2】树的分支过多
  • 解法：对树做一些修剪，比如只使用部分样本；限制树的高度，不要那么多分支。
• AdaBoost-DTree：使用的是pruned tree，将较弱的树结合起来，得到最好的G，避免出现专制。
• AdaBoost-DTree：AdaBoost+sampling+pruned DTree

高度为1时就是AdaBoost-Stump(切割)

• 限制树高为1？
• 整棵树两个分支，一次切割即可
• 此时的AdaBoost-DTree就跟AdaBoost-Stump没什么两样
• AdaBoost-Stump是AdaBoost-DTree的一种特殊情况

目标优化函数及求解

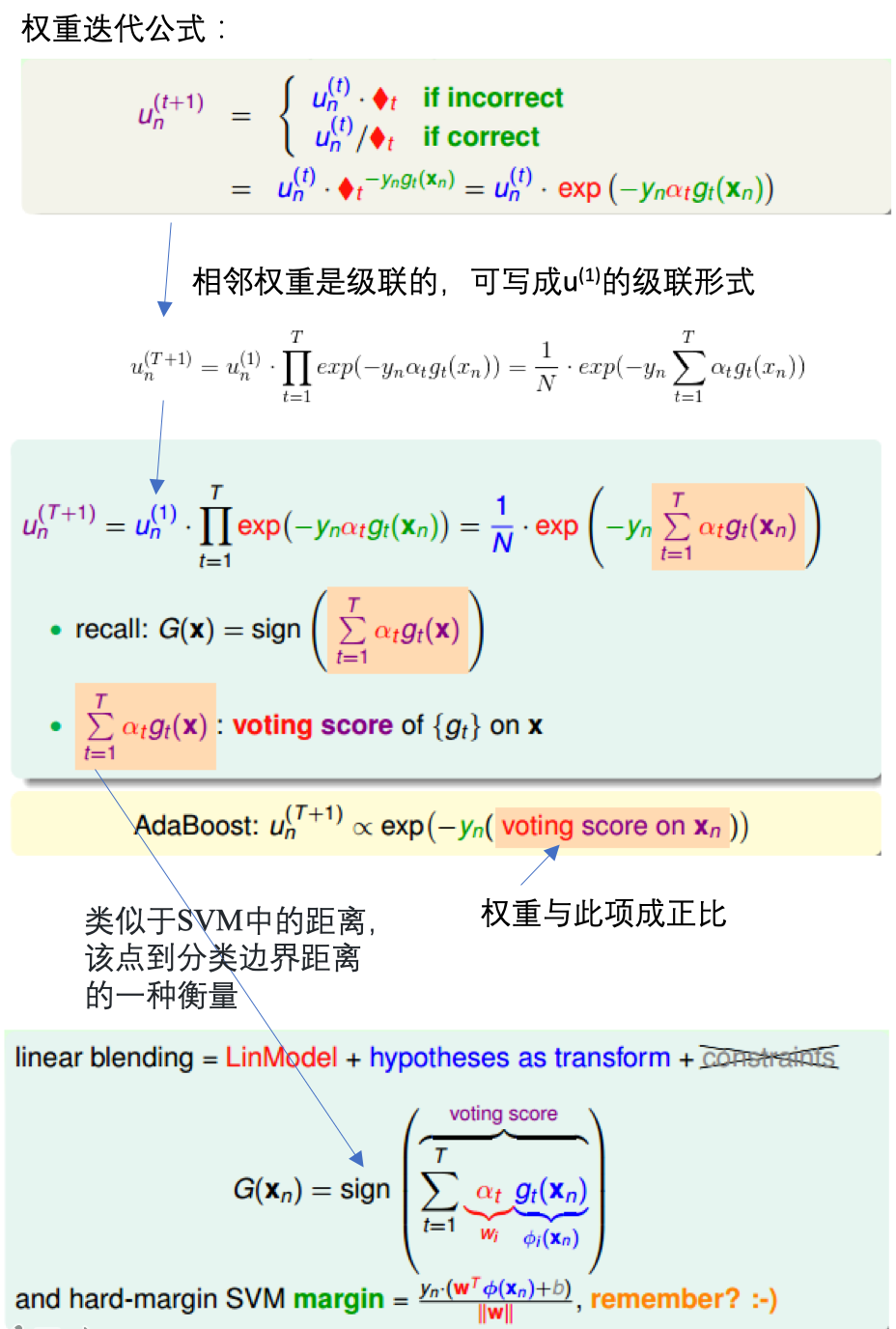
先由单个数据的权重更新，到整体样本的更新，推出需要使得最小化的函数：

通过梯度递减，求解使得满足函数最小时的模型\(g_t\)和每个决策树的权重\(\alpha_t\)：

二分类扩展到普遍

sklearn调用AdaBoost

from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.ensemble import AdaBoostClassifier

X, y = load_iris(return_X_y=True)
clf = AdaBoostClassifier(n_estimators=100)
scores = cross_val_score(clf, X, y, cv=5)
scores.mean()

梯度上升决策树

• 把上面的概念都合并起来，得到一个新的算法：梯度上升决策树。
• 那里用到了决策树？在对N个点\((x_n, y_n-s_n)\)进行回归时使用了，决策树也是可以用于回归的。
• GBDT：gradient boost + decision tree

具体步骤：

• 初始化：\(s_1=s_2=...=s_n=0\)
• 每轮迭代：方向函数\(g_t\)通过CART算法做回归求得
• 步长通过简单线性回归求解
• 更新每轮的\(s_n：s_n=s_n+\alpha_tg_t(x_n)\)
• T轮迭代结束，得到最终模型：\(G(x)=\sum_{i=1}^T\alpha_tg_t(x)\)

sklearn调用GBDT

# 分类
from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier

X, y = make_hastie_10_2(random_state=0)
X_train, X_test = X[:2000], X[2000:]
y_train, y_test = y[:2000], y[2000:]

clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
    max_depth=1, random_state=0).fit(X_train, y_train)
clf.score(X_test, y_test)

# 回归
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor

X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
X_train, X_test = X[:200], X[200:]
y_train, y_test = y[:200], y[200:]
est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
    max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
mean_squared_error(y_test, est.predict(X_test))

aggregation模型总结

5种aggregation方法

• 7.blending and bagging
• 8.adaptive boosting
• 9.decision tree
• 10.random forest
• 11.gradient boosted decision tree

blending（混合）：单个模型已知

blending：将所有已知的\(g_t\) aggregate起来，得到G，通常有3种：

• uniform：简单地计算所有\(g_t\)的平均值。投票，求平均，更注重稳定性。
• non-uniform：所有\(g_t\)的线性组合。追求更复杂的模型，存在过拟合风险。
• conditional：所有\(g_t\)的非线性组合。追求更复杂的模型，存在过拟合风险。

learning：单个模型未知

learning：一边学\(g_t\)，一边将他们结合起来，通常有3种（与blending对应）：

• bagging：通过boostrap方法，得到不同的\(g_t\)，计算所有\(g_t\)的平均值
• AdaBoost：通过boostrap方法，得到不同的\(g_t\)，所有\(g_t\)的线性组合
• decision tree：通过数据分割的形式得到不同的\(g_t\)，所有\(g_t\)的非线性组合

learning中的aggregate模型的再组合

对于aggregate模型，可以进行再次组合，以得到更强大的模型：

aggregation优点

• 防止欠拟合：把弱的\(g_t\)结合起来，以获得较好的G，相当于是feature转换，获得复杂的模型。
• 防止过拟合：把所有的\(g_t\)结合起来，容易得到一个比较中庸的模型，利用平均化，避免一些极端情况的发生。

参考

• Gradient Boosted Decision Tree