目录

• 目录
• K-近邻学习
• 低维嵌入
• 多维缩放（MDS）
• 主成分分析
• 核化线性降维、KPCA
• 流形学习
  • 等度量映射
  • 局部线性嵌入
• 度量学习
• 参考

K-近邻学习

• 常用的监督式学习方法。具体算法参见另一篇博文：K-近邻算法
• 分类：投票法；回归：平均法
• 懒惰学习的代表：lazy learning
  • 没有显示的训练过程
  • 在训练阶段保存样本，训练开销为0
  • 收到测试样本后再进行处理
• 急切学习：eager learning
  • 在训练阶段就对样本进行学习处理的方法
• 重要参数：
  • k取值：取值不同，可能结果也不同
  • 距离计算方式不同，找出的近邻可能不同。【这也是为什么在这一章会开始讲述k近邻，因为涉及距离的度量和计算】
• KNN特殊的二分类问题：
  • k=1，即1NN
  • 测试样本\(x\)，最近邻样本为\(z\)
  • 最近邻样本分类出错的概率：\(x\)与\(z\)的类别标记不同的概率，\(P(err)=1-\sum_{c\in {y}} P(c\|x)P(c\|z)\)
  • 假设：
    • 样本独立同分布
    • 对任意\(x\)和任意小正数\(\delta\)，在\(x\)附近\(\delta\)距离范围内，总能找到一个训练样本【在任意近的范围内总能找到一个训练样本】
    • \(c^*=argmax_{c\in {y}}P(c\|x)\)：贝叶斯最优分类器结果
  • 结论：最近邻分类器虽然简单，但是其泛化错误率不超过贝叶斯最优分类器的错误率的两倍。

低维嵌入

• 1NN特殊的二分类问题：重要假设是，对任意\(x\)和任意小正数\(\delta\)，在\(x\)附近\(\delta\)距离范围内，总能找到一个训练样本，即训练样本的采样密度足够大 =》密采样（dense sampling）
• 现实难以满足
• 如果\(\delta=0.001\)，只有1个属性，则需1000个点平均才能满足，如果有多个属性呢？样本巨大！=》密采样条件所需样本数一般无法达到。
• 维数灾难：curse of dimensionality，高维情形下出现的数据样本系数、距离计算困难
• 解决方案：降维
  • 维数简约
  • 通过某种数学变换将原始高维属性空间转变为一个低维子空间
  • 子空间中样本密度大幅提高，距离计算更为容易
  • 为什么可以降维？很多时候数据是高维的，但是与学习的任务有关的信息也许只是某个低维的分布：高维中的一个低维嵌入（embedding），比如三位空间的样本点在二维中更易分隔：

多维缩放（MDS）

• 多维缩放：multiple dimensional scaling，MDS
• 经典的降维方法
• 要求：原始空间中样本之间的距离在低维空间中得以保持
• 定义：
  • 原始空间：\(距离矩阵D\in R^{m\times m}, m个样本, dist_{ij}: x_i和x_j之间的距离\)
  • 目标：\(降维后的空间Z\in R^{d'\times m}，d‘空间中的距离=原始空间的，\|\|z_i-z_j\|\|=dist_{ij}\)

• 算法：

• 线性降维方法：基于线性变换来进行降维，都符合基本形式：\(Z=W^TX\)

• 不同：对低维子空间的性质有不同的要求，即对\(W\)施加了不同的约束

• 降维效果评估：
  • 比较降维前后学习器的性能，若性能有所提高则认为降维起到了作用【这么。。？】
  • 若维数将至二或者三维，可借助可视化技术直观判断降维效果

主成分分析

• 最常用降维方法。具体可参见另一篇博文[CS229] 14: Dimensionality Reduction
• 问题：对于正交属性空间的样本，如何用一个超平面对所有样本进行恰当表达？
  • 若存在，具有以下两个性质
  • 【1】最近重构性。样本点到这个超平面的距离足够近。
  • 【2】最大可分性。样本点在这个超平面上的投影尽可能分开。
  • 上面两个能分别得到主成分分析的等价推导。
• 算法：

核化线性降维、KPCA

• 线性降维：假设从高维到低维空间的函数映射是线性的
• 现实：需要非线性映射才能找到恰当的低维嵌入
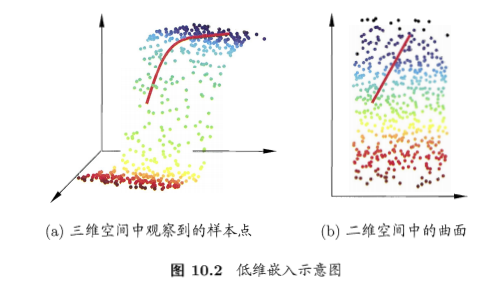
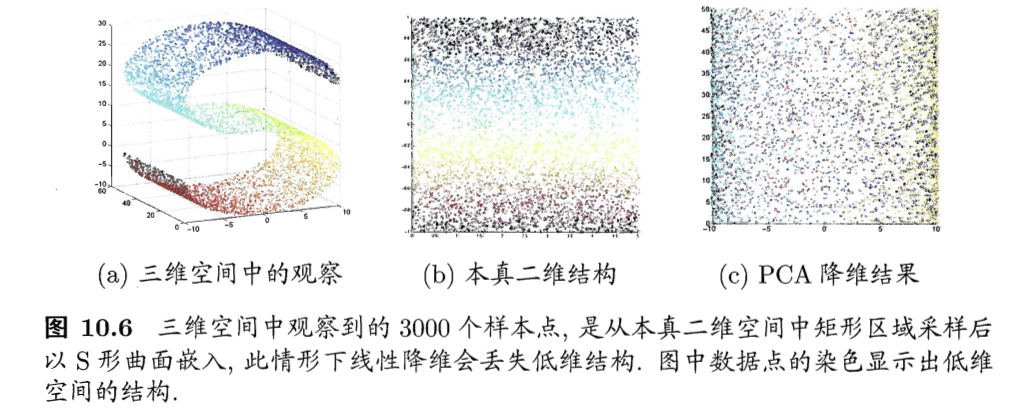
• 例子：二维采样以S曲面投到3维，如果使用线性降维（c图的PCA），则会丢失掉二维空间原本的信息

• 非线性降维：基于核技巧对线性降维方法进行核化(kernelized)

• KPCA：核主成分分析，对线性降维的PCA进行核化
• PCA求解：\((\sum_{i=1}^mz_iz_i^T)W= \lambda W\)
• \(z_i\)是\(x_i\)在高维特征中的像，则：\(W=\frac{1}{\lambda}(\sum_{i=1}^mz_iz_i^T)W=\sum_{i=1}^mz_i\frac{z_i^TW}{\lambda}=\sum_{i=1}^mz_i\alpha_i, 其中\alpha_i=\frac{1}{\lambda}z_i^TW\)
• 假设\(z_i\)是原始空间样本点\(x_i\)通过映射\(\phi\)产生，即\(z_i=\phi(x_i)\)
• 若\(\phi\)能被显式的表达出来，则通过它将样本映射到高维空间，再在特征空间中实施PCA即可
• 引入\(\phi\)后有：
  • 求解：\((\sum_{i=1}^m\phi(x_i)\phi(x_i)^T)W= \lambda W, W=\sum_{i=1}^m\phi(x_i)\alpha_i\)
  • 不清楚\(\phi\)形式，引入核函数
  • 有：\(\kappa(x_i,x_j)=\phi(x_i)^T\phi(x_j)\)
  • \(KA=\lambda A, K为\kappa的核矩阵\)，属于特征值分解问题，取\(K\)最大的\(d'\)个特征值对应的特征向量即可
• 为获得投影后的坐标，KPCA需对所有样本求和，计算开销大

流形学习

• 流形学习：manifold learning
• 借鉴拓扑流形的概念
• 流形：在局部与欧式空间同坯的空间。在局部具有欧式空间的性质，能用欧式距离进行计算。
• 启发：
  • 若低维流形嵌入到高维，虽然整体很杂乱，但是局部仍然具有欧式空间的性质。
  • 高维中局部建立降维的映射关系，再设法将局部映射关系推广到全局

等度量映射

• 等度量映射：isometric mapping，Isomap
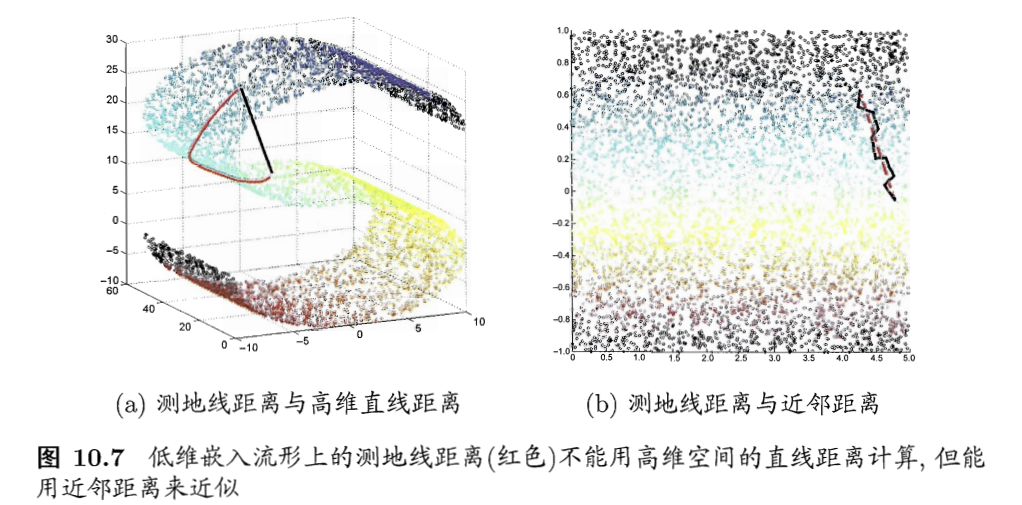
• 基础：认为低维流形嵌入到高维之后，直接在高维空间中计算直线距离具有误导性，因为在高维空间中直线距离在低维嵌入流形上是不可达的
• 例子：
  • 低维流形嵌入：距离是测地线，一只虫子从一点爬到另一点
  • 高维中不具有直连性，所以不能在高维中直接计算直线距离
• 如何计算测地线距离？
  • 流形在局部是可以计算的性质
  • 对于每个点基于欧式距离找出近邻点
  • 建立近邻连接图，邻近点存在连接，非邻近点不存在连接
  • 地线距离 =》邻近连接图上两点的最短路径问题
  • 最短路径：可采用经典的Dijkstra算法或者Floyd算法

• 算法：

• 注意：
  • 得到的是训练样本在低维空间的坐标
  • 新样本，如何映射？【不是基于流形性质获得了映射关系吗？不能直接使用吗？】
  • 训练一个回归学习器，预测新样本在低维空间的坐标
• 近邻图构建：
  • k近邻图：指定近邻点个数
  • \(\epsilon\)近邻图：指定距离阈值，小于阈值的认为是近邻点

局部线性嵌入

• Isomap：保持近邻样本之间的距离一样
• 局部线性嵌入：locally linear embedding, LLE，保持邻域内样本之间的线性关系
• 样本点\(x_i\)的坐标可通过邻域点表示： \(x_i=w_{ij}x_j+w_{ik}x_k+w_{il}x_l\)，LLE希望这个关系能在低维空间中保持
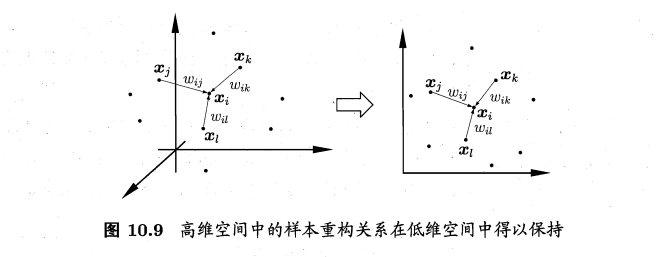
• 算法：

度量学习

• 度量学习：metric learning
• 高维 =》低维，低维空间学习性能更好
• 每个空间（高维或者低维），对应了样本属性上定义的一个距离度量
• 寻找合适空间 =》寻找合适度量

• 能否学习一个合适的距离度量？

• 距离度量表达形式，便于学习的？
• 需要有可调节的参数

参考

• 机器学习周志华第10章