目录

• 目录
• mini-batch梯度下降
• 理解mini-batch梯度下降？
• 指数加权平均
• 理解指数加权平均数
• 指数加权平均的偏差修正
• 动量梯度下降法
• RMSprop
• Adam优化算法
• 学习速率衰减
• 局部最优问题
• 参考

mini-batch梯度下降

• 优化算法：神经网络运行更快
• mini-batch vs batch：
  • batch：对整个训练集执行梯度下降
  • mini-batch：把训练集分割为小一点的子集，每次对其中一个子集执行梯度下降
  • 比如有5000000个样本，每1000个样本作为一个子集，那么可得到5000个子集
  • 用括号右上标表示：\(X^{\{1\}},...,X^{\{5000\}}\)
• 训练：
  • 训练和之前的batch梯度下降一致，只不过现在的样本是在每一个子集上进行

  • 对于每一个batch，前向传播计算，计算Z，A，损失函数，再反向传播，计算梯度，更新参数 =》 这是完成一个min-batch样本的操作，比如这里是1000个样本

  • 遍历完所有的batch（这里是5000），就完成了一次所有样本的遍历，称为“一代”，也就是一个epoc
  • batch：一次遍历训练集做一个梯度下降
  • mini-batch：一次遍历训练集做batch-num个（这里是5000）梯度下降
  • 运行会更快

理解mini-batch梯度下降？

• 成本函数比较？
  • 两者的成本函数如下：
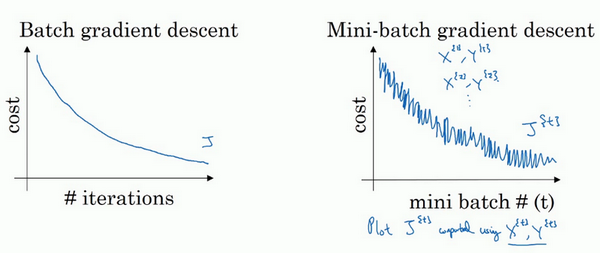
  • 可以看到，整体的趋势都是随着迭代次数增加在不断降低的
  • 但是batch情况下是单调下降的，而mini-batch则会出现波动性，有的mini-batch是上升的
  • 为什么有的mini-batch是上升的？有的是比较难计算的min-batch，会导致成本变高（那为啥还要min-batch？因为快呀！！！）。
• mini-batch size：
  • 看两个极端情况
  • size=m：batch梯度下降

  • size=1：随机梯度下降

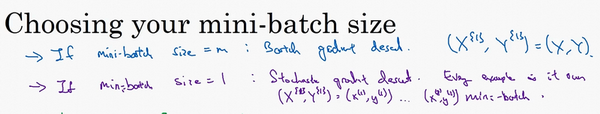
  • 收敛情况不同：
  • batch梯度下降：会收敛到最小，但是比较慢【蓝色】
  • 随机梯度下降：不会收敛到最小，在最小附近波动【紫色】

  • 合适的mini-batch梯度下降：较快的速度收敛到最小【绿色】

  • 小训练集：m<2000，使用batch梯度下降即可
  • 大训练集：mini-batch一般选为2的n次方的数目，比如64，128，256。64-512比较常见。

指数加权平均

• 还有一些比mini-batach梯度下降更快的算法
• 基础是指数加权平均
• 核心公式：\(v_t = \beta v_{t-1}+(1-\beta)\theta_t\)

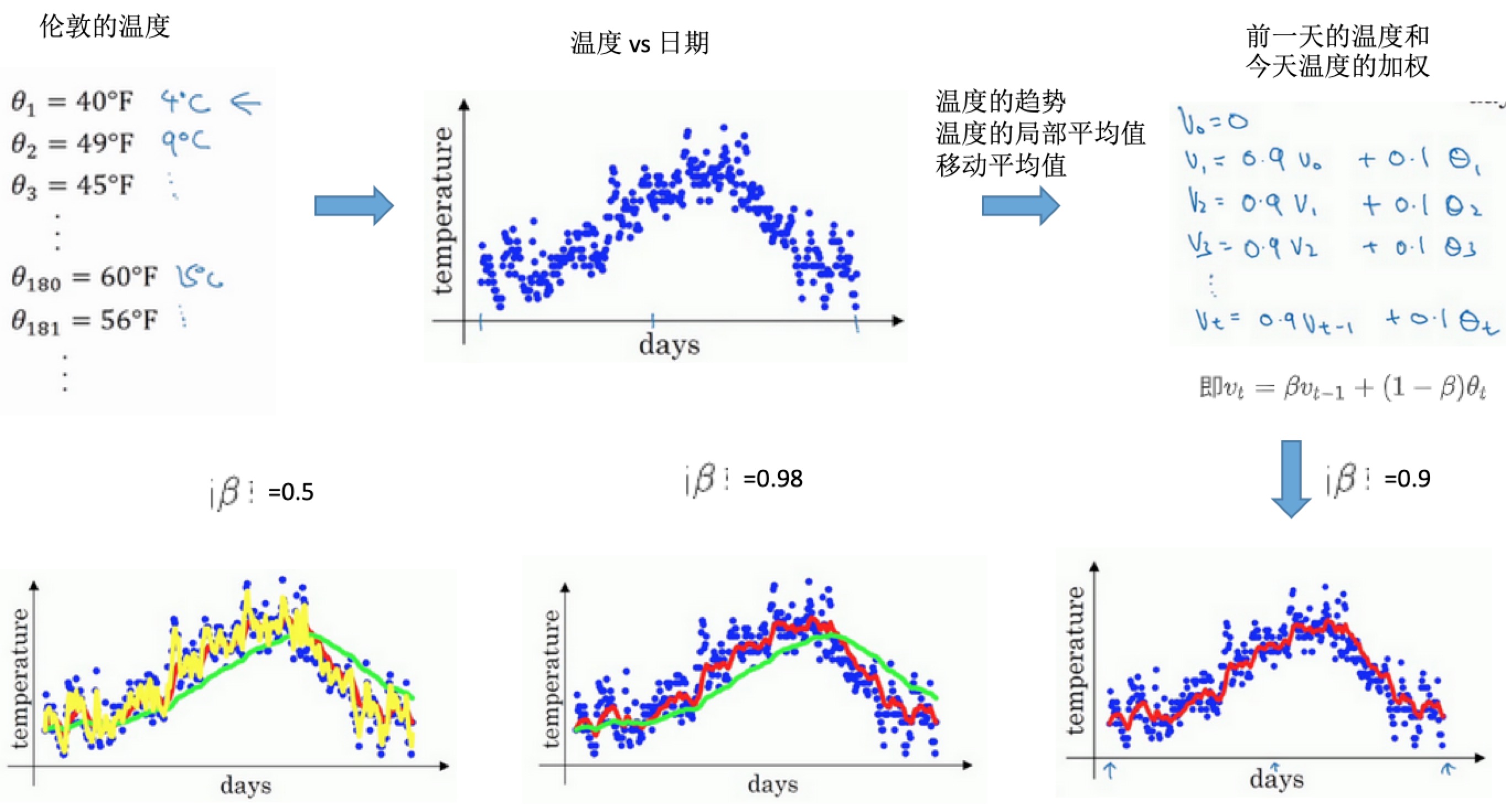
• 得到的是指数加权平均数
• 表示：大概是\(\frac{1}{1-\beta}\)天的平均温度
• 比如\(\beta=0.9\)时，是\(\frac{1}{1-0.9}=10\)天的平均值（上图红线部分）
• 比如\(\beta=0.98\)时，是\(\frac{1}{1-0.98}=50\)天的平均值（上图绿线部分）
  • 因为是更多天的平均值，所以曲线波动小，更加平坦。
  • 曲线向右移动，因为需要平均的温度值更多
  • 如果温度变化，适应温度会更慢一点，出现延迟，因为前一天权重太大(0.98)，当天温度权重太小(0.02)
• 比如\(\beta=0.5\)时，是\(\frac{1}{1-0.5}=2\)天的平均值（上图黄线部分）。平均数据较少，所以曲线有更多的噪声，有可能出现异常值。

理解指数加权平均数

• 加和平均的过程：
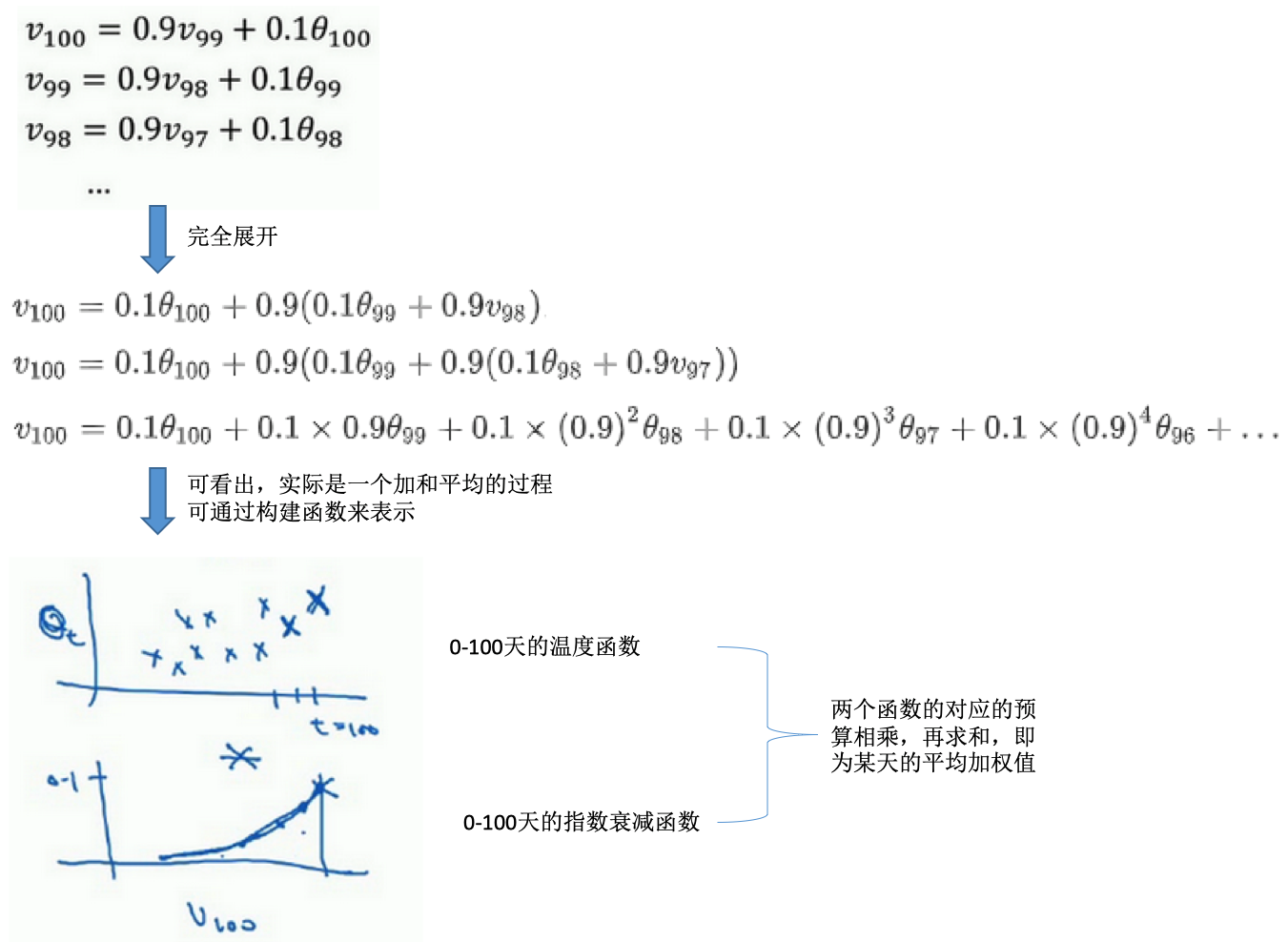
• 需要(表示)多少天的平均？
  • 大概是\(\frac{1}{1-\beta}\)天的平均温度
  • 如果\(\beta=0.9\)时，是\(\frac{1}{1-0.9}=10\)天的平均
  • 此时，第10天0.9^10=0.35，约等于1/e(e是自然对数)，也就是说10天后，曲线的高度下降到1/3，相当于峰值的1/e
• 实际计算：
  • 一开始将\(V_0\)设置为0
  • 再计算第一天\(v_1\)，第二天\(v_2\)等。【所以第一天是等于\(1-\beta \theta\)温度值】
• 为什么指数加权平均？
  • 占用极少内存
  • 电脑中值占用一行数字，然后把最新的数据代入公式计算
  • 一行代码
  • 并不是最好或者最精确的计算平均数的方法

指数加权平均的偏差修正

• 偏差修正：让平均数的运算更加准确
• 修正策略：
  • 主要是初期的估算不准确
  • 在初期不直接使用Vt，而是除以了一个系数之后的值
  • 所以当t比较大的时候，紫线和绿线会重合。偏差修正可以让在开始的阶段两者也能近似重合。
• 实际：不在乎执行偏差修正，宁愿熬过初始时期

动量梯度下降法

• 运行速度几乎总快于标准的梯度下降
• 基本思想：计算梯度的指数加权平均，利用这个梯度更新权重
• 例子：
  • 横轴希望能快速下降
  • 纵轴希望较小波动

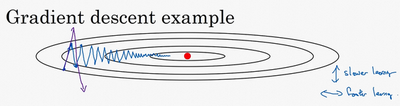
  • 使用移动平均数，计算w和b的梯度，可减缓梯度下降的幅度

  • 为什么这里梯度的移动平均是work的？
  • 纵轴：导数上下晃动，但是摆动的平均值接近于0。所以取移动平均后，正负相互抵消，使得平均值接近于0。
  • 横轴：所有的导数都是正方向的，所以平均后的值仍然很大。
  • 最终：纵轴的摆动变小，横轴的运动更快，从而在抵达最小值的路上减小了摆动。
• 算法过程：
  • 两参数：学习速率\(\alpha\)、参数\(\beta\)(控制着指数加权平均，常用值为0.9，相当于过去10此迭代的梯度的平均)
  • 一般不会做偏差修正：10此迭代之后，移动平均已经过了初始阶段

RMSprop

• RMSprop：root mean square prop
• 加速梯度下降
• 在某次迭代：
  • 计算w、b的梯度
  • 计算指数加权的值，w、b的微分平方的指数加权平均
  • 使用梯度除以上面的指数加权，进行梯度更新（不像momentum，直接使用微分的指数加权进行更新）
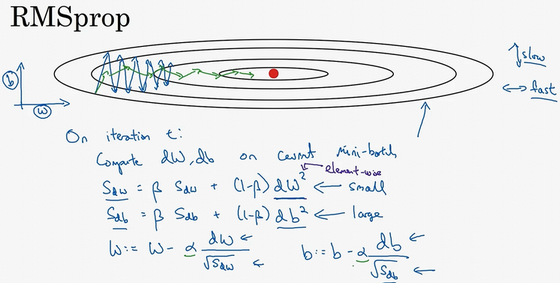
• 为什么有效果？
  • 目标：水平方向（w方向），想保持大的梯度下降；竖直方向（b方向），想减缓摆动
  • 如何做到：引入一个系数，就是原来的梯度除以一个系数
  • 原来：\(W := W - \alpha dW, b := b - \alpha db\)
  • 现在：\(W := W - \alpha \frac{dW}{sqrt(S_{dW})}, b := b - \alpha \frac{db}{sqrt(S_{db})}\)
  • 水平w方向：斜率较小，所以dW较小
  • 竖直b方向：斜率较大，所以db较大
  • 结果：纵轴更新被一个大的数相除，消除摆动；水平更新则被小的数相除。在图中就是由蓝色的线变为绿色的线，纵轴摆动小，横轴继续推进。【核心：消除有摆动的方向，所以更快】

Adam优化算法

• 结合Momentum和RMSprop
• Adam：adaptive moment estimation，Adam权威算法
• 过程：
  • 初始化
  • 迭代时
    • 先计算mini-batch的w、b的梯度
    • 计算momentum指数加权平均，更新超参数\(\beta_1\)
    • 计算RMSprop加权平均，更新超参数\(\beta_2\)
    • 基于上述两者更新权重w和b
  • 图解
• 超参数：
  • 学习速率：\(\alpha\)，需要调试
  • dW的移动平均数：参数\(\beta_1\)，momentum项，缺省值是0.9
  • \((dW)^2,(db)^2\)的移动平均：参数\(\beta_2\)，RMSprop项，推荐使用0.99
  • 超参数\(epsilon\)：选择没那么重要，建议是10^-8

学习速率衰减

• 随时间减少学习速率可加快学习算法
• 比较：
  • 学习速率固定：蓝色线，整体会朝向最小值，但是不会精确收敛，因为mini-batch有噪声所以最后在最小值附近摆动
  • 学习速率慢慢减小：绿色线，初期是学习速率较大，学习相对较快；随着学习速率的减小，会在最小值附近的一块区域摆动，而不是在训练中来回摆动。
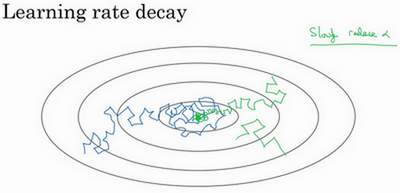
• 本质：学习初期，能承受较大的步伐；但当开始收敛的时候，小的学习速率能让步伐小一些。
• 如何设置：
  • 设置为依赖于epoch的：\(\alpha=\frac{1}{1+decay_rate \times epoch_num}\)

  • decay_rate：需调整的超参数

  • 例子：decay_rate=1, \(\alpha_0=0.2\)
  • 第一代（epoch1）：\(\frac{1}{1+1*1}\alpha_0=0.1\)
  • 第二代：0.67
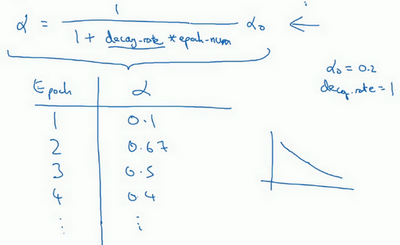
• 其他衰减函数：
  • 指数衰减：epoch_num作为指数
  • 离散下降：不同的阶段学习速率减小一半
  • 手动衰减

局部最优问题

• 梯度为0通常不是局部最优，而是鞍点
  • 高维空间概率局部最优概率很小：假设梯度为0，那么每个方向可能是凸函数，也可能是凹函数。要想是局部最优，需要每个方向都是凸函数，概率是2^(n)，如果是高维空间，这个概率值很小。所以更可能碰到的是鞍点。
  • 为什么叫鞍点？有一点导数为0.
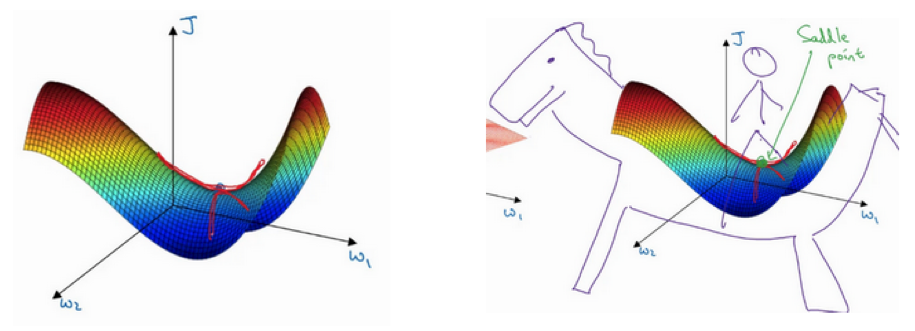
  • 所以局部最优不是问题
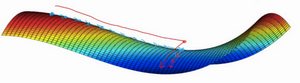
• 平稳段学习减缓：
  • 局部最优不是问题
  • 平稳段导数长时间接近于0，曲面很平坦
  • 学习十分缓慢，这也是Momentum、RMSprop、Adam能加速学习的地方
  • 需要很长的时间才能走出平稳段

参考

• 第二周：优化算法
• Sebastian Ruder: An overview of gradient descent optimization algorithms 一个比较不同的梯度下降优化算法的文章