目录
- 目录
- 调试过程
- 为超参数选择合适的范围
- 超参数调试:熊猫 vs 鱼子酱
- 归一化网络的激活函数
- Batch归一化拟合到神经网络中
- Batch归一化为什么有效?
- 测试时的batch归一化
- Softmax回归
- 训练一个softmax分类器
- 深度学习框架
- TensorFlow
- 参考
调试过程
- 超参数:
- 某些超参数比其他的更重要
- 【1】需调试的最重要的超参数:
- 学习速率
- 【2】仅次于\(\alpha\)的参数:
- Momentum参数\(\beta\):一般使用默认值0.9
- 隐藏单元的数目
- mini-batch size
- 【3】其他因素:
- 隐藏层数目
- 学习速率的衰减率
- 【4】最不重要
- Adam算法里面的参数:\(\beta_1, \beta_2, \varepsilon\),一般使用默认值:0.9,0.999,10^-8
- 如何选择超参数呢?
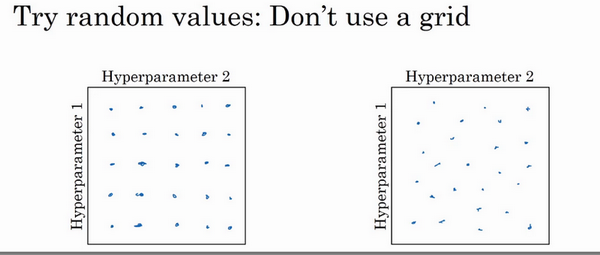
- 核心1:随机选择点,不要网格搜索
- 网格搜索:当参数的数量相对较少时,很实用
- 随机选择:深度学习领域推荐使用此方法
- 为啥随机搜索?
- 比如只有2个参数:学习速率\(\alpha\)和Adam参数\(\varepsilon\),显然前者比后者重要得多。
- 当选择同等数量的点进行调试时,【1】网格搜索:实验了5个不同的\(\alpha\),但是\(\varepsilon\)取任何值效果是一样的。【2】随机选择:可能取到了独立的25个\(\alpha\)值,就更可能发现选择哪一个更好。
- 实际:三个甚至更多的超参数
-
随机取值而不是网格取值表明,你探究了更多重要的超参数的潜在值
- 核心2:由粗糙到精细的策略
- 比如在两个参数时,随机取了一些点,发现某个区域整体效果都还不错
- 接下来可以放大这块区域,然后更密集的随机取值
为超参数选择合适的范围
- 随机取值:
- 在超参数范围内可提升搜索效率
- 但不是均匀取值
- 而是选择合适的尺寸
- 有的参数可以随机(均匀)选取:
- 在范围内可以随机均匀选取
- 比如隐藏单元数目、层数

- 有的参数不能随机(均匀)选取:
- 不能线性的随机取
- 比如学习速率\(\alpha\):假设其范围是0.0001-1之间有最优,如果画一条范围直线随机均匀选取,则90%选取的值在0.1-1之间,10%在0.0001-0.1之间,这看上去是有问题的。
- 可用对数尺度去搜索:不使用线性的,依次取0.0001,0.001,0.01,0.1,1,然后在此对数数轴上均匀选取,这样资源才比较均等
- 具体:在\([10^a,10^b]\)之间取值,需要做的就是在[a,b]之间均匀取值(比如为r),然后取的超参数值=\(10^r\)
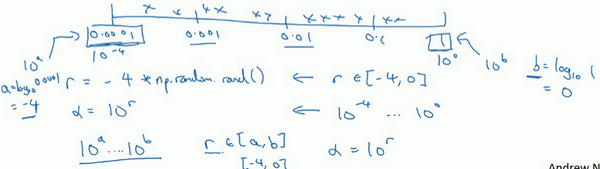
-
在对数坐标下取值,取最小的对数就得到a的值,取最大的对数就得到b值。在a,b间随意均匀的选取r值,再设置为\(10^r\)即可。
- 如何给Momentum的\(\beta\)取值?指数的加权平均
- 假如搜索区间是0.9-0.999
- 不能用线性轴,可探究\(1-\beta\)
- 当\(\beta:0.9-0.999\)时,\(1-\beta:0.1-0.001\),换为对数轴取值,在[-3,-1]之间均匀取值为r,然后超参数值\(1-\beta=10^r,\beta=1-10^r\)

超参数调试:熊猫 vs 鱼子酱
- 深度学习应用领域广泛,但是超参数的设定会随时间变化而变化,比如添加了新的数据等。建议:至少每隔几个月,重新测试或评估模型的超参数,以确保对数值已然很满意。
- 如何搜索超参数?
- 两种流派
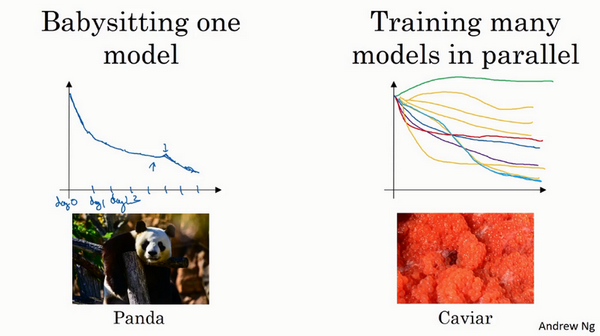
- 照看模式:随机化选择参数,一次实验一个,看效果。有的时候损失随着参数的更新一直在下降,突然某个时候可能又上升了。
- 熊猫方式:孩子很少,一次通常就一个
- 同时实验多种模型:平行实验许多不同的模型,最后快速选择效果最好的那个。
-
鱼子酱模式:繁殖的时候会产生很多卵
- 选择哪种?
- 取决于拥有的计算资源
- 如果足够多,选择鱼子酱模式
- 两种流派
归一化网络的激活函数
- Batch归一化
- 深度学习一个重要的算法
- 使得参数搜索问题变得容易
- 神经网络对超参数的选择更稳定
- 超参数的范围更庞大
- 特征值的归一化
- 特征值的归一化:减去平均值,除以方差
- 逻辑回归或者神经网络都可以用到这个
- 能加快学习过程
- 把学习的轮廓从很长的东西变成很圆的

- 激活值能否归一化?
- 对于更深的模型
- 特征值:输入层到第一个隐藏层
- 激活值:其他隐藏层之间的传递值,每一层的激活值a作为下一层的输入
- 试想:特征值的归一化是可以提高训练速度的,那么如果激活值也是归一化的,是不是也能提升训练速度呢?
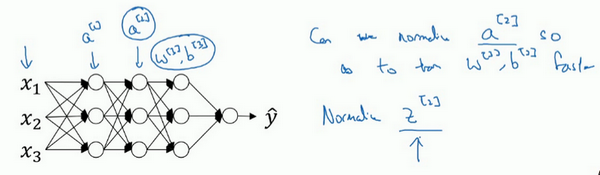
- z值的归一化:
- 我们通常选择归一化z,就是激活函数的输入值,而不是激活后的值【激活前z值的归一化】
-
把隐藏层的z值标准化,化为平均值为0和标准单位方差的值
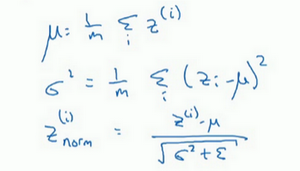
- 是否一定需要归一化为:均值为0,单位方差?
- 不一定!如果分布是有意义的,可以选择其他的值。
- 做法:不直接使用归一化的值,可以在归一化的值进行参数添加以控制,\(\widetilde{z}^{(i)} = \gamma z_{norm}^{(i)}+\beta\),这里控制的两个参数是需要进行设定的,就像Momentum里面的参数一样,也会在梯度下降中进行更新
-
可以看到,当满足:\(\gamma=sqrt(\sigma^2+\epsilon), \beta=\mu\)时,就是上面的均值为0,标准方差的归一化了
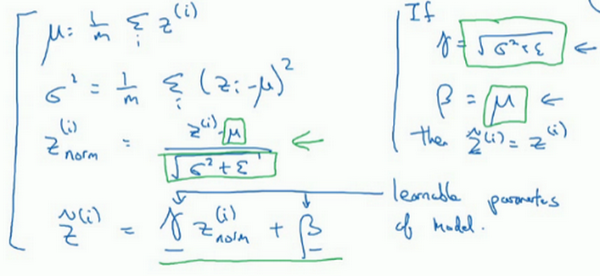
- 特征输入、隐藏单元区别:一般特征输入是归一化到平均值为0方差为1,但是隐藏神经元可以不一定是这个值,这一点就是通过引入的两个参数进行控制的
- 比如对于sigmoid函数,不像其归一化后的值总是在0附近,因为这样是趋于线性的
Batch归一化拟合到神经网络中
- Batch归一化是发生在计算
z和a之间的:- 输入层特征值通过与第一层之间的w、b参数,得到第一层的z
- 然后对z进行归一化,得到\(\widetilde{z}\)
- 对\(\widetilde{z}\)用激活函数计算a
- 以此类推
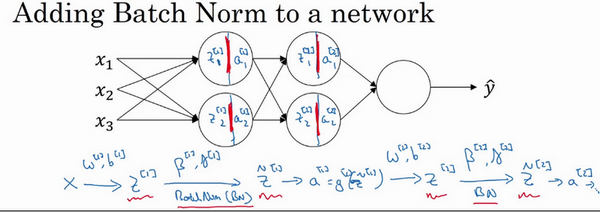
- 注意:这里每一层都是单独归一化的,所以每一层都有自己的参数:\(\\gamma, \beta\)
- Batch归一化通常和mini-batch一起使用
- 每一次对一个batch进行前向传播、归一化、反向传播、梯度下降等
- 参数b是被减去的:\(z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}\),归一化需要均值为0标准方差,再由参数\(\gamma, \beta\)进行缩放。所以\(b^{[l]}\)的值是被减去的。通过参数\(\beta^{[l]}\)进行控制,产生偏移或偏置。
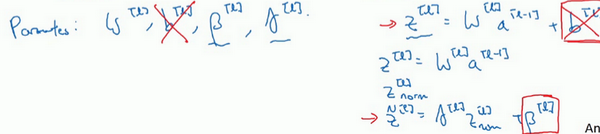
- 梯度下降更新:
- 对于batch归一化涉及的参数也要进行更新

- 对于batch归一化涉及的参数也要进行更新
Batch归一化为什么有效?
- 原因1:类比特征值归一化
- 做特征值归一化类似的工作,只不过对象是隐藏单元值
- 原因2:权重比网络更滞后或更深层
-
比如第10层的权重相比第1层的权重更能经受住变化(分布的变化等)
- 背景是:数据分布的变化对于网络使有影响的,需要重新许梿学习算法
- 例子:左边训练黑猫的模型,训练好了,现在应用于有色猫的识别
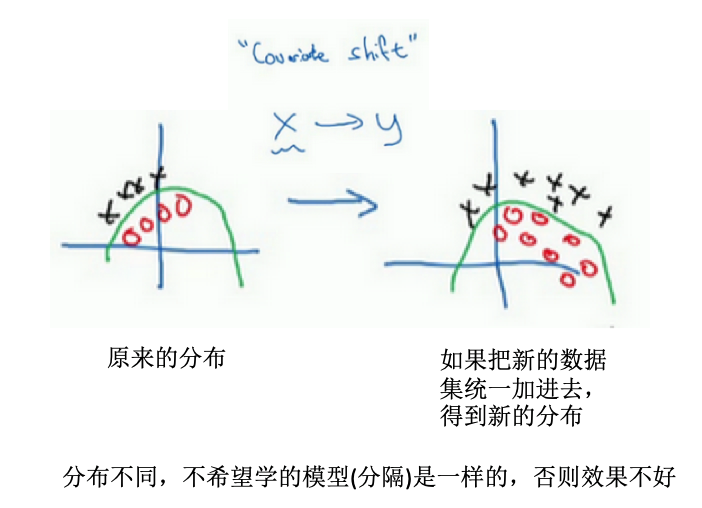
-
covariate shift:如果已经学习了x到y的映射,如果x的分布改变了,那么可能需要重新训练你的学习算法
- 为什么在神经网络中这是个问题?
- 某一层的激活值,在计算上直接与前一层的值有关,但是如果前面一些层的参数都发生了改变,那么这些隐藏单元的值也是在不断改变的,就有了上面的covariate shift问题
- batch归一化:减少隐藏值分布的变化,也许具体的z的值会变化,但是至少均值和方差分别是0和1.因此可以减少值的改变的问题,使这些值更加的稳定。
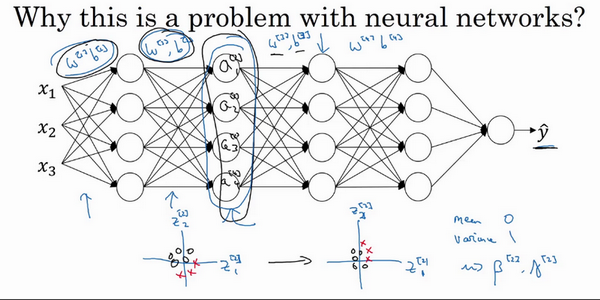
- 浅层不会左右移动那么多,因为被同样的均值和方差所限制,从而使得后层的学习更加容易。
-
- Batch归一化还有正则化的效果:
- 每个mini-batch上进行归一化,由均值和方差进行缩放
- 均值和方差是有一些噪声的:因为只是某一个mini-batch所计算出来的
- 结果:在隐藏层的激活值上增加了噪音。标准偏差的缩放和减去均值带来的额外噪音。
- dropout:也是增加噪音,隐藏单元以一定的概率乘以0或者1,应用较大的mini-batch可以减少正则化效果。
- 分析:标准偏差的缩放和减去均值带来的额外噪音。使得后部分的神经元不过度依赖于任何一个隐藏单元,所以有轻微的正则化效果。效果没有dropout那么强。

测试时的batch归一化
- 训练:以mini-batch的形式进行
- 测试:不能将一个mini-batch的样本同时处理,因为每次只是预测一个样本(此时均值和方差没有意义)。
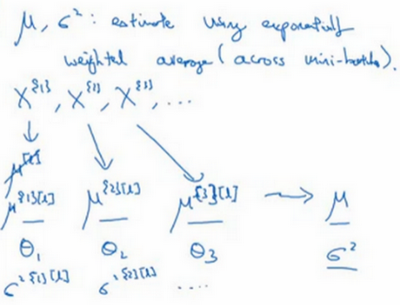
- 方法:为了将神经网络运用于测试,需要单独估算平均值和方差
- 原理:使用指数加权平均对均值和方差进行追踪,以计算指数加权平均值
- 具体:对于某一层l,有很多个mini-batch,每一个mini-batch都可以计算均值和方差。然后使用指数加权平均计算均值和方差,这个均值和方差就是在测试的时候用到的。
Softmax回归
- 二分类:标记是0和1
- softmax回归:
- 多分类的一种
- 不止识别两个分类
- 例子:
- 识别图片中的是猫、够、小鸡

- 输出:一个向量,表示了每一个类别的概率
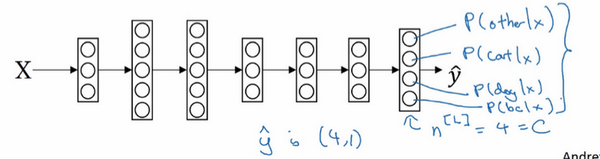
- 识别图片中的是猫、够、小鸡
- 为什么能做到多分类?
- softmax层+输出层实现
- softmax:对所有元素求幂,然后每个求幂元素的除以总的幂元素和(归一化),得到对应的幂指数数值的概率
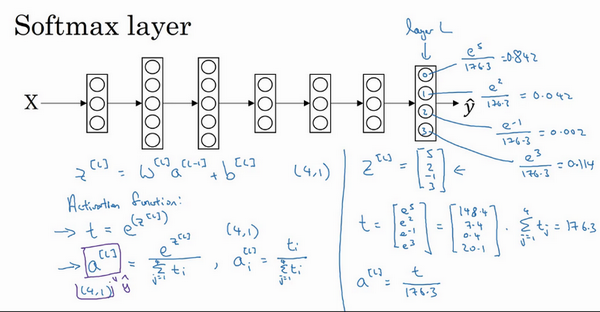
- 求幂指数概率的过程可看成是一个激活函数
- softmax激活函数:将所有可能的输出归一化,所以输入一个向量,输出也是一个向量,能够实现多分类
- softmax分类器:
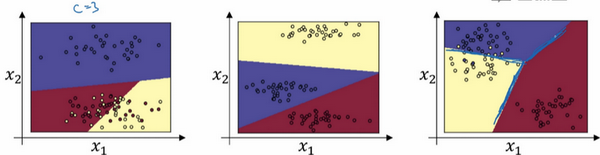
- 还能干什么?实现多类的线性划分
- 例子:没有中间隐藏层的网络,输入层+softmax层+输出层
- 可以看到,当类别数=3时,一个softmax层可以实现线性决策边界的划分。同样的,对于其他能够两两之间线性分隔的,都可以在多分类的情况下被softmax分类器区分开来。
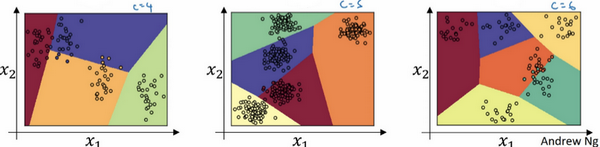
- 在类别数目C=5或者6的时候,也是可以实现的
训练一个softmax分类器
- softmax vs hardmx:
- softmax: 指数归一化,输出的是概率向量,更为温和的映射
- hardmax:观察向量中的元素,最大的元素置为1,其他元素置为0.
- 比如下面,对于softamx计算出来的向量,对应的hardmax向量则是:[1 0 0 0]

- softmax回归 vs logistic回归:
- 前者是将逻辑回归的激活函数推广到C类
- 当C=2时,softmax实际上变回了逻辑回归

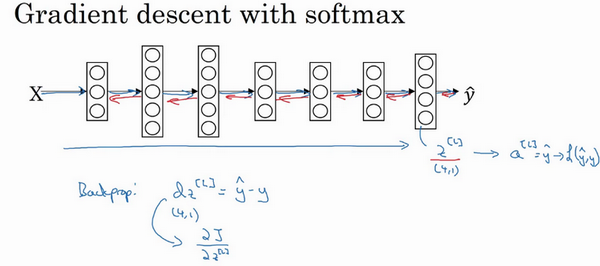
- 单个样本损失函数:
- 形式:\(L(\hat{y}, y)=-\sum_{i=1}^{10} y_l log{\hat{y}_j}\)
- 例子:如果真实标签是[0 1 0 0],表示一个猫的照片。输出向量 a=[0.3 0.2 0.1 0.4],从概率来看,在猫的概率值不是最大的,所以在这个样本的预测上效果不好。
- 直接从损失函数理解:因为y1,y3,y4都=0,只有y2=1,所以\(L(\hat{y}, y)=-y_2log(\hat{y}_2)=-log(\hat{y}_2)\),如果要损失函数越小,则对应的预测值\(\hat{y}_2\)应该越大越好,就是预测为第2类(猫)的概率值越大越好。
- 损失函数:找到训练集中的真实类别,然后使该类别相应的概率尽可能的高。
- 多样本的损失:
- 整个训练集损失的总和:
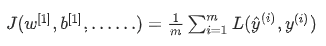
- 整个训练集损失的总和:
- 梯度下降最小化损失函数:
- 反向传播求导
- 导数:\(dz^{[l]}=\hat{y}-y)\),导数还是一个C维的向量
深度学习框架
- 从零开始实现模型不现实
- 框架:通过提供比数值线性代数库更高程度的抽象化,使得在开发深度学习应用时更加高效
- 如何选择框架:
- 便于编程
- 运行速度
- 真的是开源的,能有良好的管理

TensorFlow
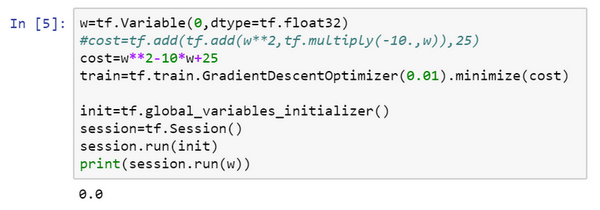
- 损失函数最小化:\(Jw=w^2-10w+25\)
import numpy as np
import tensorflow as tf
w = tf.Variable(0,dtype = tf.float32)
#接下来,让我们定义参数w,在TensorFlow中,你要用tf.Variable()来定义参数
#定义损失函数:
cost = tf.add(tf.add(w**2,tf.multiply(- 10.,w)),25)
# 使用梯度下降进行训练
#(让我们用0.01的学习率,目标是最小化损失)。
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
#最后下面的几行是惯用表达式:
init = tf.global_variables_initializer()
session = tf.Session() #这样就开启了一个TensorFlow session。
session.run(init) #来初始化全局变量。
#然后让TensorFlow评估一个变量,我们要用到:
session.run(w)
#上面的这一行将w初始化为0,并定义损失函数,我们定义train为学习算法,它用梯度下降法优化器使损失函数最小化,但实际上我们还没有运行学习算法
print(session.run(w))
# 0
session.run(train)
print(session.run(w))
# 0.1
for i in range(1000):
session.run(train)
print(session.run(w))
# 4.9999
# 结果很接近5了
- 定义cost函数的不同方式:
- 使用符号:add,multiply等
- 写公式:直接
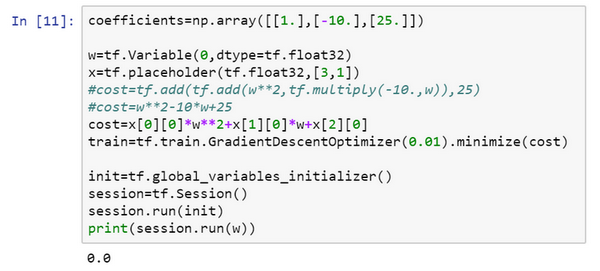
- placeholder:
- 之后会赋值的变量
- 告诉tf,会稍后为x提供数值
- 数据的占位:这里是对于损失函数的系数,直接使用一个向量x进行占位,所以在写损失函数的时候从x里面取值。然后再把定义的值feed到x
- 很方便的对更改系数值,相当于是一个函数了,比如把系数改为其他的值,那么此时最小化的是另外一个损失函数了,但是我们大体的代码是不便的。
- 使用with进行session的打开:
- 更方便清理
- 更常用

- tf核心:
- 计算损失函数,然后自动计算导数,及最小化损失
- 相当于建立计算图
- 通过计算损失,实现前向传播
- 不需要明确实现反向传播
参考
If you link this blog, please refer to this page, thanks!
Post link:https://tsinghua-gongjing.github.io/posts/improve-deep-neural-networks-2-hyperparameter.html
Previous:
【2-2】深度学习的算法优化
Next:
【3-1】机器学习(ML)策略(1)
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me