Home > MachineLearning > Main text

【2-1】深度学习的实践层面：数据集、正则化、梯度

Tag: python, machine learning
2019-01-27

目录

数据集：训练、验证、测试集

  • 训练神经网络时的一些决策：
    • 多少层
    • 每层的隐层单元的数目
    • 学习速率选择多少
    • 每层采用什么激活函数
  • 高度迭代的过程：
    • 想法：不同的参数设置等
    • 编程
    • 运行查看结果
    • 基于结构完善，提出新的想法
  • 最佳决策取决于：
    • 数据量
    • 计算机配置中输入特征的数量
    • GPU还是CPU进行训练
  • 项目进度的关键：
    • 循环迭代过程的效率
    • 一个可行的方案：创建高质量的训练、验证和测试数据集

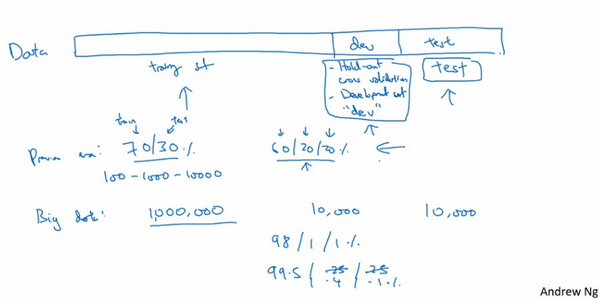
  • 数据集划分：
    • 流程：对训练集执行算法，通过验证集选择最好的模型，经过验证后，选定最好的模型。在测试集上进行评估，为了无偏评估算法的运行状况。 * 训练集
    • 验证集

    • 测试集

    • 小数据量：
      • 常见：三七分，70%训练集，30%测试集
      • 最近认可的：60%训练集，20%验证集，20%测试集
      • 数据量：100，1000或者10000条，划分是合理的
    • 大数据量：
      • 验证+测试：倾向于比例更小
      • 验证集：检测哪种算法更有效，不需要20%的数据作为验证集
      • 数据量：比如百万级别
      • 100万数据：1万验证，1万测试 =》98%训练集，1%验证集，1%测试集
      • 超过百万的：训练集99.5%，验证测试各0.25%，或者验证0.4%测试0.1%即可
  • 训练和测试集不匹配：
    • 深度学习的趋势
    • 不匹配是指数据来源不匹配，导导致数据分布不匹配
    • 不是正负样本失衡这种
    • 验证集和测试集最好来自同一个分布
  • 测试集要不要？
    • 测试集目的：对最终选定的神经网络系统做出无偏估计
    • 如果不需要无偏估计，可以不设置测试集
    • 只有训练集+验证集：训练集训练，尝试不同模型，验证集评估，迭代选出最合适的即可。因为验证集已涵盖测试集数据，不再提供无偏估计。

偏差和方差

  • 机器学习：偏差和方差易学难精
  • 深度学习：对偏差和方差的权衡研究很浅
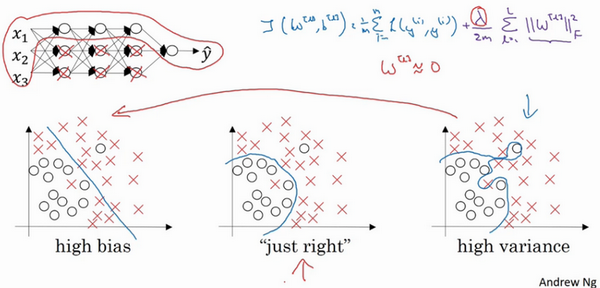
  • 二维例子：
    • 高偏差：直线拟合，不能很好的拟合数据，出现高偏差，也是欠拟合
    • 高方差：复杂神经网络拟合，但是数据过度拟合，即过拟合
    • 复杂程度适中的分类器
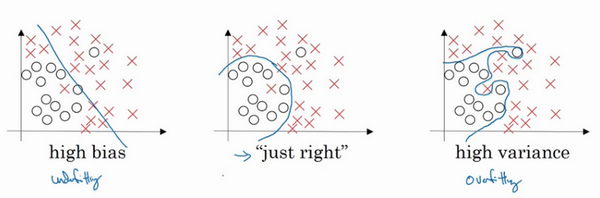
    • 这里是二维特征，可可视化研究，现实中的高维，如何判断？不同的指标

指标：训练集误差和验证集误差

  • 训练集误差1%，验证集误差11%：训练很好，验证相对差，可能是模型过度拟合训练集，验证集没有利用其交叉验证的作用 =》 高方差
  • 训练集误差15%，验证集误差16%：训练数据拟合度不高，是欠拟合的 =》 高偏差。在验证集上的结果是合理的，因为和训练误差相差不大。
  • 训练集误差15%，验证集误差30%：训练数据拟合度不高，同时在验证集上效果也很差 =》 高偏差+高方差

  • 训练集误差0.5%，验证集误差1%：效果很好，偏差和方差都很低。

  • 例子：
    • 直线：高偏差（拟合效果差）
    • 中间扭曲、两端直线：高偏差+高方差，高偏差因为其整体还是直线，区分效果差；高方差是因为中间拟合对了两个样本【有些区域偏差大，有些区域方差大】
    • 二次曲线：效果挺好

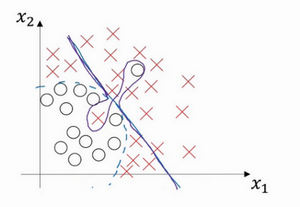
偏差方差应对

  • 偏差高：
    • 一般是看训练集，也同时看一下验证集效果
    • 方案：选择新模型，更多层，更多隐藏单元，更先进的优化算法，延长训练时间
    • 最低标准：不断尝试上面的方法，消除偏差问题，直到可以拟合数据，至少是拟合训练集数据
  • 方差高：
    • 一般是验证集上的性能查看方差大小
    • 方案：更多的数据、正则化
  • 注意：
    • 高偏差和高方差是不同的。比如是高偏差问题，增多数据也没多少用处。
    • 偏差和方差权衡。机器学习阶段讨论较多，因为有较多的方法，深度学习则不然。

正则化

  • 过拟合（高偏差）：
    • 更多数据：可靠但是成本太高
    • 正则化：减少网络误差，避免过拟合
  • 范数：
    • 关于范数的介绍可参考这里：几种范数的简单介绍
    • L0范数：向量x中非零元素的个数
    • L1范数：\(\|\|x\|\|_1=\sum_i\|x_i\|\)，非零元素的绝对值之和。也称为“稀疏规则算子”。
    • L2范数：\(\|\|x\|\|_2=\sqrt{\sum_ix_i^2}\)，元素的平方和再开方。也称为“岭回归”或者“权重衰减”。
    • L-∞范数：\(\|\|x\|\|_\infty=max(\|x_i\|)\)，向量元素的最大值
  • 线性回归正则化：
    • L1正则化：Lasso回归
    • L2正则化：Ridge回归（岭回归）
  • 逻辑回归正则化：
    • L1正则化：w最终会是稀疏的，很多值是0。间接实现特征选择，适合于特征有关联的情况。
    • L2正则化：很多w接近于0，使得优化求解稳定快速，适合特征间没有关联的情况。使用的是范数平方。
  • 神经网络正则化：
    • 正则化：范数平方
    • 正则化矩阵范数称为“弗罗贝尼乌斯范数”，用F标注：其实使用的是L2范数
    • 矩阵中所有元素的平方和
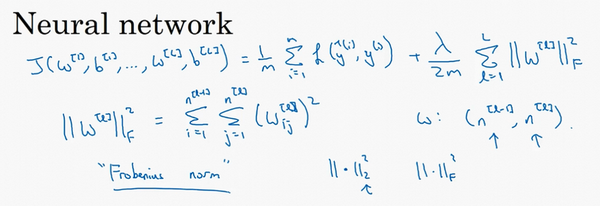
  • 加入正则化后的权重衰减：
    • 正则化项会影响梯度的计算
    • 之前：权重 = 权重 - 学习率x导数
    • 现在：权重 = 系数x权重 - 学习率x导数， 这里的系数就是一个小于1的数值（一般alpha很小，m很大，整体值在0.95-0.99之间），所以每次更新时权重都会先乘以一个小于1的系数，权重是在不算的衰减的。20190819162827

正则化为什么可减少过拟合？

  • 基于网络神经元的理解：
    • 如果开始是过拟合（高方差）的状态：
    • 当\(\lambda\)很大，权重会接近于0，可理解为很多隐藏神经元权重设置为0，这部分神经元会被消除。整个网络变为一个很简单的网络，小到如同一个神经元，但是深度很大，此时会从过拟合转变为左边的欠拟合（高偏差）的状态。
    • 当\(\lambda\)取值合适，能得到一个中间的状态。
    • 直观理解：很多神经元的权重会很低，这些神经元对于网络的影响很小，整个的神经网络变得简单，所以不容易发生过拟合。
  • 基于激活函数的理解：
    • 如果\(\lambda\)很大，整体损失很小，那么权重w很小
    • 权重很小时，z也会很小
    • 如果z的范围很小，比如都在靠近0的地方，那么当激活函数是tanh的时候，g(z)大致是线性的
    • 每层都是线性的话，就和线性回归函数类似
    • 线性网络，不是一个极复杂的非线性函数，从而不会发生过拟合
  • 这里列举了一些关于正则化L1/L2的原理、为什么有效果、不同的模型中有何效果的问题，可以参考一下。

dropout正则化

  • dropout正则化：
    • 随机失活
    • 非常实用
    • 遍历网络的每一层，设置消除神经网络结点的概率
    • 设置完成后，会消除一些结点及对应结点的连线，从而得到一个更小规模的网络，在进行反向传播训练
  • 例子：
    • 一个样本，每个节点以0.5概率失活 20190819165058
    • 对其他样本，同样操作，失活一些节点，保留一些结点【失活保留的可能是不一样的】
    • 如果对每个样本训练的是规模极小的网络，那么也不容易发生过拟合的
  • 如何实现dropout？
    • 常见：反向随机失活（inverted dropout）
    • 阈值参数：keep-prob，表示隐藏单元保留的概率
    • 对于每一层的节点，随机生一个和节点数目相等的向量，然后比较每个位置的数值与上面的阈值的大小，如果高于这个阈值，此节点设置为1（保留），否则设置为0（消除）。得到一个判断向量。
    • 然后 激活函数 = 激活函数x判断向量，这样更新后的激活函数值，就可以把判断为0（消除）的节点的数值元素归为0.
    • 最后 激活函数=激活函数/keep-prob，得到修正后的激活函数值，因为此时的激活函数值是要作为下一层的输入的，如果不想改变下一层的期望值，就需要进行弥补操作。比如第3层50个节点，80%概率保留，\(z^4=w^4a^3+b^4\)，其中\(a^3\)减少了20%（有20%元素被归为0），为了不影响\(z^4\)期望（或者说确保\(a^3\)的期望不变），需要\(w^4a^3/0.8\)以弥补所需的20%。
  • 在测试阶段，不需要使用dropout

为什么dropout有用？

  • 基于特征权重的理解：
    • 不依赖于任何特征，因为其输入随时可能被清除
    • 权重会比较均匀的传播下去，能达到权重收缩的平方范数的效果
    • 类似于L2正则化
  • 设置方案1：参数keep-prob：
    • 表示每一层上保留单元的概率
    • 不同的层可以变化
    • 有的层节点较多，过拟合可能严重，可以设置较小的值
    • 有的层节点较少，过拟合不严重，可以把该值设置的高一些
    • 如果某层不担心过拟合，可以设置为1
    • 此时的设置有点像L2正则化中的\(\lambda\)
    • 缺点：搜索更多的超参数
  • 设置方案2：
    • 某些层应用dropout，某些层不使用
  • dropout：
    • 计算机视觉：用的多，输入量很大，输入太多像素，没有足够的数据，容易过拟合
    • 只是一种正则化方法，有助于预防过拟合
    • 除非算法过拟合，不然不使用
    • 缺点：代价函数J不再被明确定义

其他正则化方法

  • 已介绍：
    • L2正则化
    • dropout
  • 还有：
    • 数据扩增
      • 动物识别：可以水平翻转，裁剪等操作
      • 光学字符：添加数字，随意扭曲或旋转
      • 这种方式比较廉价
    • early stop
      • 绘制训练和验证误差
      • 一般训练集误差随着迭代次数进行一直下降
      • 验证集误差刚开始是下降的，在某个点后开始上升
      • 找到这个中间点，然后停止迭代
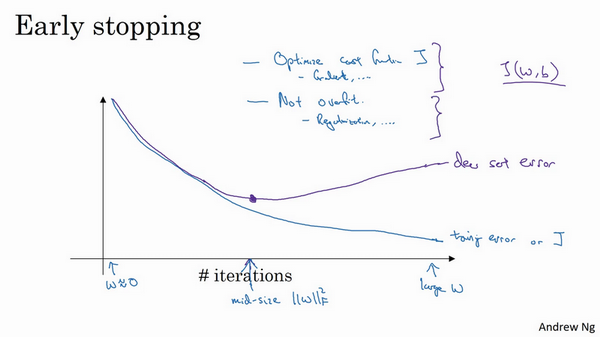
      • 优点：只运行一次梯度下降，，可以找出w的较小值、中间值和较大值，无需尝试L2正则化参数\(\lambda\)的很多值

归一化输入

  • 加速训练：归一化输入
    • 【1】零均值：求特征的均值，x减去对应的均值。是移动数据集的操作，直到完成零均值化。
    • 【2】归一化方差：求每个特征方差\(\sigma^2\)，数据除以方差。
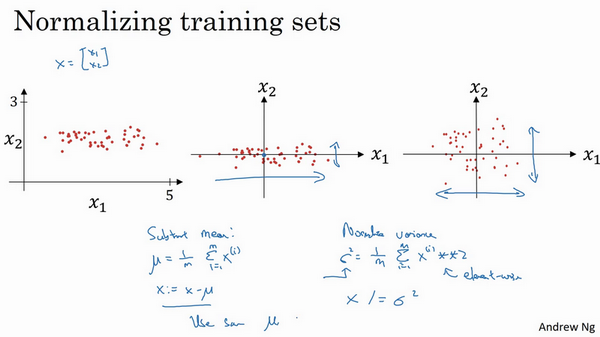
  • 注意：
    • 用训练集相同的均值和方差去归一化测试集
    • 不能在训练集和测试集上分别预估均值和方差
  • 为什么要归一化？
    • 当不同的特征值范围差异很大时，代价函数不是圆的
    • 当特征值都在相近的范围，代价函数会更容易优化
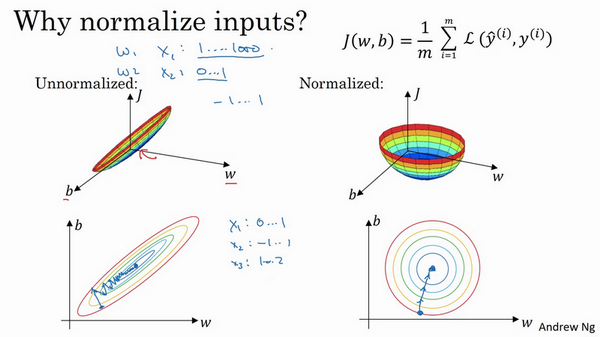
    • 执行归一化不会产生危害，通常会做归一化处理

梯度消失/爆炸

  • 梯度消失或爆炸：
    • 训练神经网络的时候，导数有时会变得非常大或者非常小，甚至以指数方式变小，加大了训练的难度
  • 例子：
    • 一个多层，每层两个结点的神经网络
    • 激活函数：g(z)=z，线性激活函数
    • 忽略b
    • 输入x，输出y：\(y=W^{[l]}W^{[l-1]}W^{[l-2]}...W^{[2]}W^{[1]}x\)
    • 如果每个权重w一样，且\(w^{[l]}=\begin{bmatrix}1.5 & 0 \\0 & 1.5\end{bmatrix}\)，这个是1.5倍的单位矩阵，\(\hat y = 1.5^{(L-1)}x\)，是呈指数级增长的，y的值将爆炸式增长
    • 如果权重是0.5，即\(w^{[l]}=\begin{bmatrix}0.5 & 0 \\0 & 0.5\end{bmatrix}\)，它比1小，\(\hat y = 0.5^{(L-1)}x\)，激活函数将以指数级下降
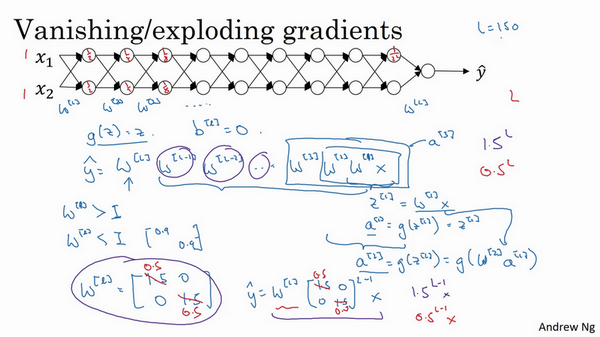
  • 权重W只比1（单位矩阵）略大一点，深度神经网络的激活函数将爆炸式增长；如果比1略小一点，深度神经网络的激活函数将指数级递减。【这个问题其实不太理解，即使后面说初始化权重，但是也不等于1，也是比1大一点的或者小一点的，不是也会出现爆炸或者消消失吗？】

神经网络权重初始化

  • 梯度爆炸或消失解决方案：权重初始化（谨慎的设置初始权重），能部分解决问题
  • 单个神经元例子：
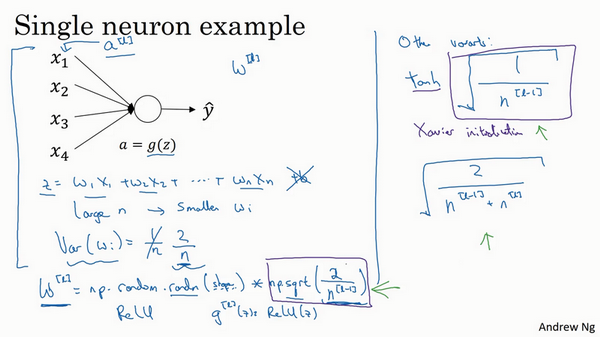
    • z是x和权重的线性组合
    • 为了预防z过大或过小，如果n越大，希望w越小。最理想的是w=1/n
    • 如果选择了ReLU激活函数，方差设置为2/n效果更好
    • 还有其他的一些变体，告诉我们当选择不同的激活函数时，初始化的权重应该是怎么样的效果比较好

梯度的数值逼近：双链误差更准确

  • 结论：双边误差公式的结果更准确
  • 在反向传播时，会做梯度检验，确保反向传播的正确性。
  • 例子：20190819204959

梯度检验

  • 对于所有的参数构建一个大的向量
  • 利用双边误差估计对于每个参数的导数
  • 反向传播计算的导数

  • 比较这两个导数值的差异，越小（一般要小于10^-7）越好 20190819205823

  • 注意：
    • 不要在训练中使用，只用于调试
    • 如果梯度检验失败（有的不符合），需检查所有项，尝试找出问题
    • 如果有正则化，在进行梯度检验时也要考虑
    • 梯度检验与dropout不能同时使用
    • 当w，b都接近于0时，梯度下降的实施是正确的。所以可以随机初始化使得w、b的值接近于0.

参考


If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/improve-deep-neural-networks-2-practical.html
Previous: 【1-4】深层神经网络
Next: keras

    Category

    Latest articles

    Links