目录

• 目录
• 深层神经网络
• 前向和反向传播
• 深度网络中的前向传播
• 核对矩阵的维数
• 为什么使用深层表示？
• 搭建神经网络模块
• 参数vs超参数
• 参考

深层神经网络

• 前面：一个隐藏层的神经网络，正向传播，反向传播，向量化，随机初始化权重
• 逻辑回归：一层的神经网络
• 有一个隐藏层的神经网络，就是一个两层神经网络。输入层不算。
• 层数：\(L\)表示
• \(L\)层激活后结果：\(a^{[l]}\)，正向传播需要计算的就是这个；激活函数：\(g\)，其输入是\(z^{[l]}\)
• 符号表示参见指南

前向和反向传播

• 前向：计算Z(基于上一层的输出)，再计算a(激活后)
• 反向：根据当前层对a的导数，计算上一层对啊的导数，以及当前层对参数w和b的导数

深度网络中的前向传播

• 一个训练样本：
  • 计算第一层z，再激活后的a
  • 计算第二层z，再激活后的a
  • 。。。
  • 计算第四层z，再激活后的a。此时的a就是最后的输出，因为第四层就是输出层了。
• 一个样本(向量化实现)：
  • 计算Z：\(Z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}\)
  • 计算激活后的a：\(A^{[l]}=g^{[l]}(Z^{[l]})(A^{[0]}=X)\)

核对矩阵的维数

• 常用检查代码方法：
  • 过一遍算法中矩阵的维数
• 参数w维度：(下一层维数，前一层维数)，\(w^{[l]}:(n^{[l]},n^{[l-1]})\)
• 参数b维度：(下一层维数，1)，\(w^{[l]}:(n^{[l]},1)\)
• z和激活后a的维度：\(z^{[l]},a^{[l]}:(n^{[l]},1)\)。输出值是下一层的结点数目。

为什么使用深层表示？

• 神经网络不一定很大，但是需要有深度，就是有比较多的隐藏层，为什么？
• 例子：
  • 人脸识别系统
  • 前面的几层是简单的探测，比如不同的层探测人脸不同的部位如眼睛边缘、鼻子侧翼等

  • 后面的层则可以探测更复杂的函数，比如眼睛、鼻子等

  • 语音识别
  • 前几层：音频波形特征，音调高低、噪声、简单的丝丝声音等
  • 后几层：声音的基本单元、单词、句子等
• 层次递进：
  • 较早的几层：学习低层次的简单特征

  • 后几层：把简单的特征组合起来，探测更复杂的东西

  • small：隐藏单元的数量相对较少
  • deep：隐藏层数目比较多
  • 如果浅层网络要表达深层同样的效果，需要指数级增长的单元数目才行
• 电路理论：
  • 不同的基本逻辑门
  • 比如计算异或或者奇偶性
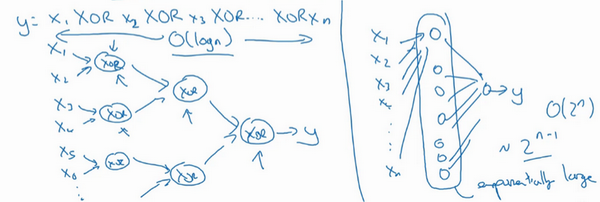
  • 异或树：或门+非门，树图的网络深度：\(O(log(n))\)，节点的数量和电路部件（门的数量）并不会很大
  • 浅层：比如单隐藏层，列举耗尽2^n种可能，需要的隐藏单元数是\(O(2^n)\)

搭建神经网络模块

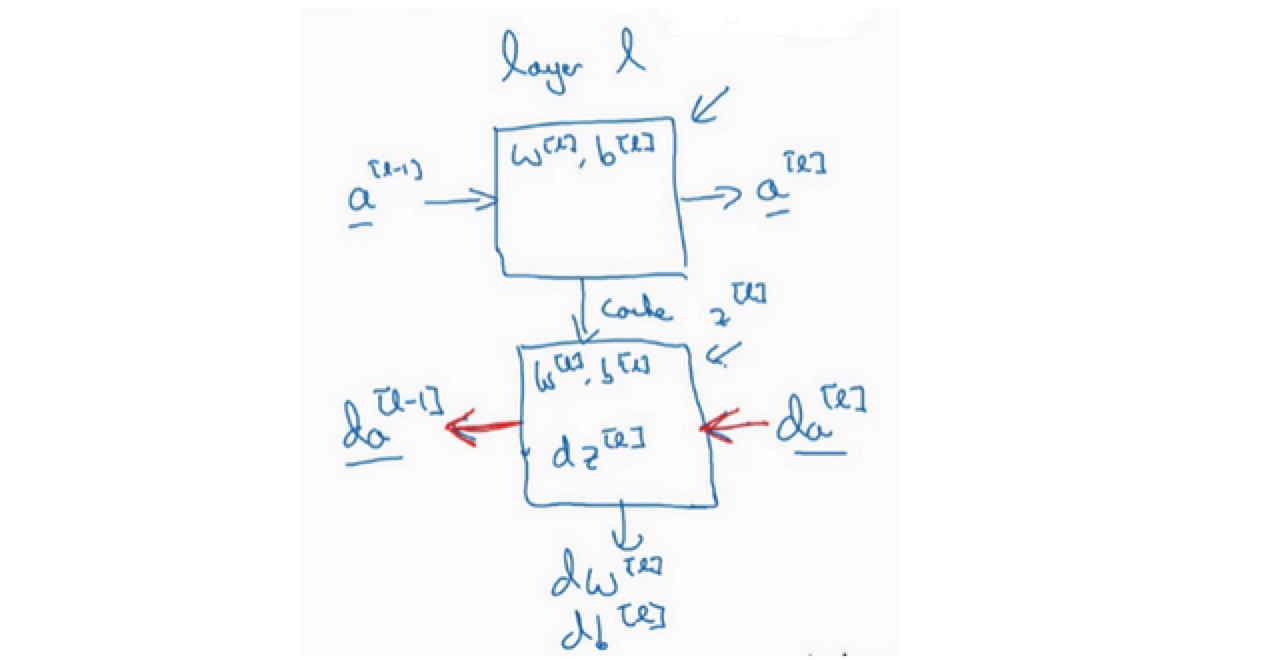
• 正向步骤：正向函数
• 反向步骤：反向函数
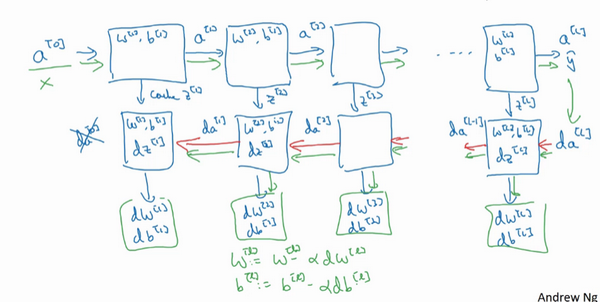
• 一步训练：
  • 前向：从\(a^{[0]}\)开始，通过正向传播计算得到\(\hat y\)
  • 反向：用输出值\(\hat y\)计算导数，从最后开始计算。得到：所有的导数项，同时，W和b在每一层也会更新

参数vs超参数

• 超参数：

  • 控制了最后的其他的参数w和b的值，所以称为超参数

  • 常见的一些超参数包含：
  • 学习速率
  • 梯度下降法循环的次数
  • 隐藏层数目
  • 隐藏层单元数目
  • 激活函数
  • momentum
  • min batch size
  • 正则化参数
• 寻找最优超参数：
  • 尝试不同的参数，实现模型并观察是否成功，然后再迭代
  • 偏于经验性
  • 必须尝试很多次不同的可能性（深度学习令人不满的一部分）
  • 有一条经验规律：经常试试不同的超参数，勤于检查结果，看看有没有更好的超参数取值，你将会得到设定超参数的直觉。

参考

• 第四周：深层神经网络