Home > MachineLearning > Main text

线性回归

Tag: python, machine learning
2018-08-27

概述

  1. 基本概念：
    • 线性回归（linear regression）：预测数值型的目标值。
    • 回归方程（regression equation）：依据输入写出一个目标值的计算公式。
    • 回归系数（regression weights）：方程中的不同特征的权重值。
    • 回归：求解回归系数的过程。
    • “回归”来历：Francis Galton在1877年，根据上一代豌豆种子的尺寸预测下一代的尺寸。没有提出回归的概念，但是采用了这个思想（或者叫研究方法）。
  2. 直接求解：
    • 找出使得误差最小的\(w\)。误差：预测值和真实值之间的差值，如果简单累加，正负将低效，一般使用平方误差。
    • 平方误差：\(\sum_{i=1}^{m}{(y_i - {x_i}^T w)^2}\)
    • 矩阵表示：\((y - Xw)^T(y-Xw)\)
    • 矩阵求导：通过对\(w\)求导（导数=\(X^T(y-Xw)\)）
    • 导数求解：当其导数=0时，即求解得到\(w\)：\(w = (X^TX)^{-1}X^Ty\)
    • 【注意】：\(X^TX^{-1}\)需要对矩阵求逆，所以只适用于逆矩阵存在的时候（需判断逆矩阵是否存在）。Numpy库含有求解的矩阵方法，称作普通最小二乘法（OLS，ordinary least squares）。
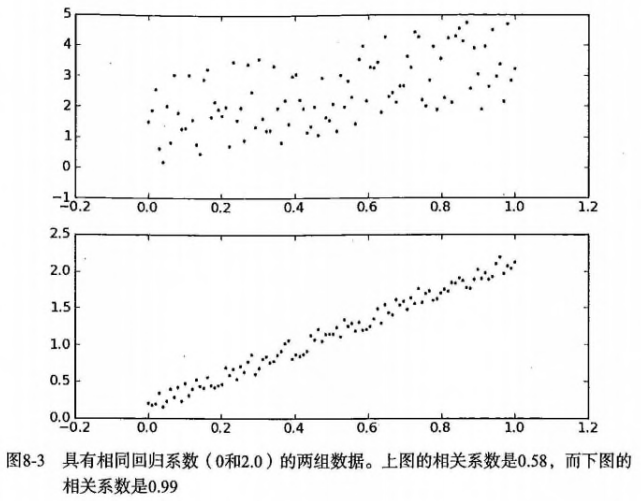
  3. 判断回归的好坏？
    • 比如两个单独的数据集，分别做线性回归，有可能得到一样的模型（一样的回归系数），但是此时回归的效果是不不一样的，如何评估？
    • 计算预测值和真实值之间的匹配程度，即相关系数。
    • Numpy的函数：corrcoef(yEstimate, yActual) regression_correlation_coefficient.png
  4. 局部加权线性回归
    • 直线拟合建模潜在问题：有可能局部数据不满足线性关系，欠拟合现象
    • 局部调整：引入偏差，降低预测的均方误差
    • 局部加权线性回归（Locally Weighted Linear Regression，LWLR）：给待预测点附近的每个点赋予一定权重，在这个子集（待预测点及附近的点）上基于最小均方差进行普通回归。
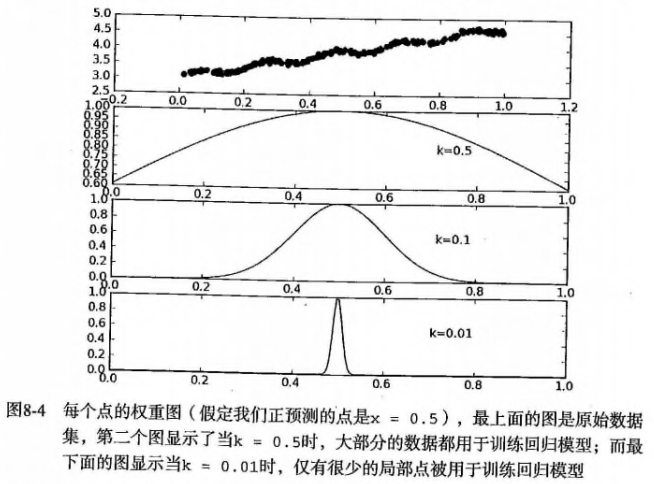
    • 使用核对附近点赋予更高权重，常用的是高斯核，其对应的权重如下： \(w(i,j) = exp{(\frac{\|x^i-x\|}{-2k^2})}\)，距离预测点越近，则权重越大。这里需要指定的是参数k（唯一需要考虑的参数），决定了对附近的点赋予多大权重。 regression_locally_weighted.png
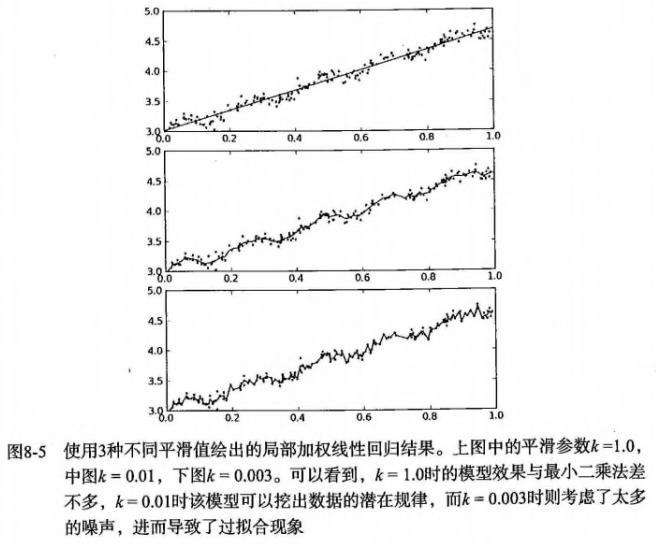
    • 使用不同的k时，局部加权（平滑）的效果是不同的，当k太小时可能会过拟合：regression_locally_weighted2.png
    • 【注意】：局部加权对于每一个预测，都需要重新计算加权值？因为输入除了x、y还需要指定预测的点（\(x_i\)），增加了计算量（但其实很多时候大部分的数据点的权重接近于0，如果可以避免这些计算，可减少运行时间）。
  5. 缩减系数

    • 问题：数据特征（n）比样本数目（m）还大（矩阵X不是满秩矩阵），怎么办？前面的方法不行，因为计算\(X^TX^{-1}\)会出错

    • 岭回归（ridge regression）：在矩阵\(X^TX\)加入\(lambda*I\)使得矩阵非奇异，从而能对\(X^T + lambda*I\)求逆矩阵。
    • I：mxm的单位矩阵，对角线元素全为1，其他全为0。值1贯穿整个对角线，在0构成的平面上形成一条1的岭，所以称为岭回归。
    • lambda：用户定义数值。可以通过不同的尝试，最后选取使得预测误差最小的lambda。
    • 回归系数：\(w = (X^TX + lambda*I)^{-1}X^Ty\)
    • 用途：1）处理特征数多于样本数的情况，2）在估计中引入偏差
    • 缩减（shrinkage）：引入参数lambda限制所有w的和，lambda作为引入的惩罚项，能减少不重要的参数，这个技术称为缩减。

    • 其他缩减方法：lasso、LAR、PCA回归、子集选择

    • lasso法：效果好、计算复杂
    • 岭回归增加如下约束则回归结果和普通回归一样：\(\sum_{k=1}^{n}w_k^2 <= lambda\)，此时限定回归系数的平方和不大于lambda。

    • lasso限定：\(\sum_{k=1}^{n}\|w_k\| <= lambda\)，使用绝对值进行限定。当lambda足够小时，很多权重值会被限定为0，从而减少特征，更好的理解数。但是同时也增加了计算的复杂度。

    • 前向逐步回归：效果与lasso接近，实现更简单。
    • 原理：每一步尽可能减少误差（贪心算法），初始化所有权重为1，每一步对某一个权重增加或减少很小的值，使得误差减小。【在随机梯度下降里面，每次是同时更新所有的权重】
    • 需要指定参数：x，y，eps（每次迭代需要调整的步长），numIt（迭代次数）
    • 好处是利于理解数据，权重接近于0的特征可能是不重要的。
  6. 权衡偏差与方差
    • 误差：预测值和测量值之间存在的差异【模型效果是否好，复杂度低效果不太好，复杂度高效果可能好偏差低】
    • 误差来源：偏差、测量误差和随机噪声
    • 缩减：增大模型偏差的例子，某些特征回归系数设为0，减少模型的复杂度
    • 方差：从总体中选取一个子集训练得到一个模型，从总体中选取另外一个子集训练得到另外一个模型，模型系数之间的差异就反应了模型方差的大小。【模型是否稳定，复杂度低则稳定，复杂度高则不稳定（过拟合的）】

实现

标准回归（可直接矩阵求解）：

# 注意判断矩阵是否可逆
def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws

标准回归(statsmodels’ module OLS and sklearn)：

import statsmodels.api as sm
 
X=df[df.columns].values
y=target['MEDV'].values
 
#add constant
X=sm.add_constant(X)
 
# build model
model=sm.OLS(y,X).fit()
 
prediction=model.predict(X)
 
print(model.summary())

from sklearn import linear_model
 
lm = linear_model.LinearRegression()
model = lm.fit(X,y)
 
y_pred = lm.predict(X)
 
lm.score(X,y)
 
lm.coef_
lm.intercept_<br><br>evaluation(y,y_pred)

局部加权线性回归：

def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))
    for j in range(m):                      #next 2 lines create weights matrix
        diffMat = testPoint - xMat[j,:]     #
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

岭回归（使用缩减技术之前，先标准化不同的特征）：

def ridgeRegres(xMat,yMat,lam=0.2):
    xTx = xMat.T*xMat
    denom = xTx + eye(shape(xMat)[1])*lam
    if linalg.det(denom) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = denom.I * (xMat.T*yMat)
    return ws
    
def ridgeTest(xArr,yArr):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean     #to eliminate X0 take mean off of Y
    #regularize X's
    xMeans = mean(xMat,0)   #calc mean then subtract it off
    xVar = var(xMat,0)      #calc variance of Xi then divide by it
    xMat = (xMat - xMeans)/xVar
    numTestPts = 30
    wMat = zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:]=ws.T
    return wMat

岭回归（sklearn）：

from sklearn.linear_model import Ridge
 
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
 
y_pred=ridge_reg.predict(X)
 
evaluation(y,y_pred,index_name='ridge_reg')

Lasso回归（sklearn）：

from sklearn.linear_model import Lasso
 
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
y_pred=lasso_reg.predict(X)
evaluation(y,y_pred,index_name='lasso_reg')

前向逐步回归：

def stageWise(xArr,yArr,eps=0.01,numIt=100):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean     #can also regularize ys but will get smaller coef
    xMat = regularize(xMat)
    m,n=shape(xMat)
    #returnMat = zeros((numIt,n)) #testing code remove
    ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
    for i in range(numIt):
        print ws.T
        lowestError = inf; 
        for j in range(n):
            for sign in [-1,1]:
                wsTest = ws.copy()
                wsTest[j] += eps*sign
                yTest = xMat*wsTest
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        #returnMat[i,:]=ws.T
    #return returnMat

多项式回归（sklearn）：

from sklearn.preprocessing import PolynomialFeatures
 
poly_reg = PolynomialFeatures(degree = 4)
X_Poly = poly_reg.fit_transform(X)
 
lin_reg_2 =linear_model.LinearRegression()
lin_reg_2.fit(X_Poly, y)
 
 
y_pred=lin_reg_2.predict(poly_reg.fit_transform(X))
 
evaluation(y,y_pred,index_name=['poly_reg'])

弹性网络回归（sklearn）：

enet_reg = linear_model.ElasticNet(l1_ratio=0.7)
 
enet_reg.fit(X,y)
 
y_pred=enet_reg.predict(X)
evaluation(y,y_pred,index_name='enet_reg ')

参考


If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/linear_regression.html
Previous: 集成算法和AdaBoost

    Category

    Latest articles

    Links