目录

• 目录
• 集成算法
  • 例子：股票推荐
  • 集成算法效果更好
  • 好的集成需要基学习器“好而不同”
  • 学习器多样性的度量
  • 学习器多样性的增强
  • 回归：多模型平均比单一模型效果更好的证明
  • 不同类别的集成算法
  • uniform blending：权重相同
  • linear blending: 权重不同的线性组合
  • stacking(any blending)：非线性组合
  • 如何得到不同的\(g_t\)
  • \(g_t\)的结合策略
• bagging vs random forest vs boosting
• AdaBoosting
• AdaBoost：Python源码版本
• AdaBoost：sklearn版本
• 参考

集成算法

例子：股票推荐

问题：多个朋友推荐股票的走势，分别是\(g_1, g_2, ..., g_t\)，如何选择（如何确定\(g_t(x)\)）？

方案：

以上每种选择其实对应一个模型：

集成算法效果更好

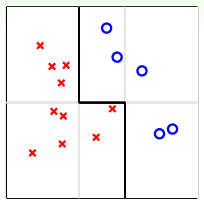
例子：平面上有需分类的点，如果只用一条水平或竖直直线进行分类，无论如何达不到最佳分类效果。可使用集体智慧，及多条线的组合，比如图中的折线（一条水平线+两条竖直线），即可将点完全分开。

为什么效果更好：

• 将不同的模型均匀结合，提高power，相当于特征转换
• 正则化效果：比如有多个模型选择，但是各种组合最后得到的是比较中庸、合适的（比如下图有很多不同的选择，但是黑色的是组合后最好的）

特征转换	正则化

好的集成需要基学习器“好而不同”

问题：一般经验中，如果把好坏的东西掺和在一起，通常会是比最坏的要好一些，比最好的要坏一些。集成学习为什么能比最好的单一学习器效果更好呢？

例子：

• （a）中每个分类器66.6%精度，集成的模型100%
• （b）中3个分类器没有差别，集成的也是一样的
• （c）每个分类器只有33.3%，集成后结果更糟糕
• 说明：好的集成，需要满足“好而不同”
  • 个体学习器要有一定的准确性，不能太坏(c)
  • 学习器之间具有差异(b)

理论分析：

• 二分类问题y={-1,1}，基分类器错误率为\(\epsilon\)
• 每个基分类器\(h_i\)有：\(P(h_i(x) \neq f(x))=\epsilon\)
• 随着集成中个体分类器数目T的增大，集成的错误率将指数级下降，最终趋向于0.

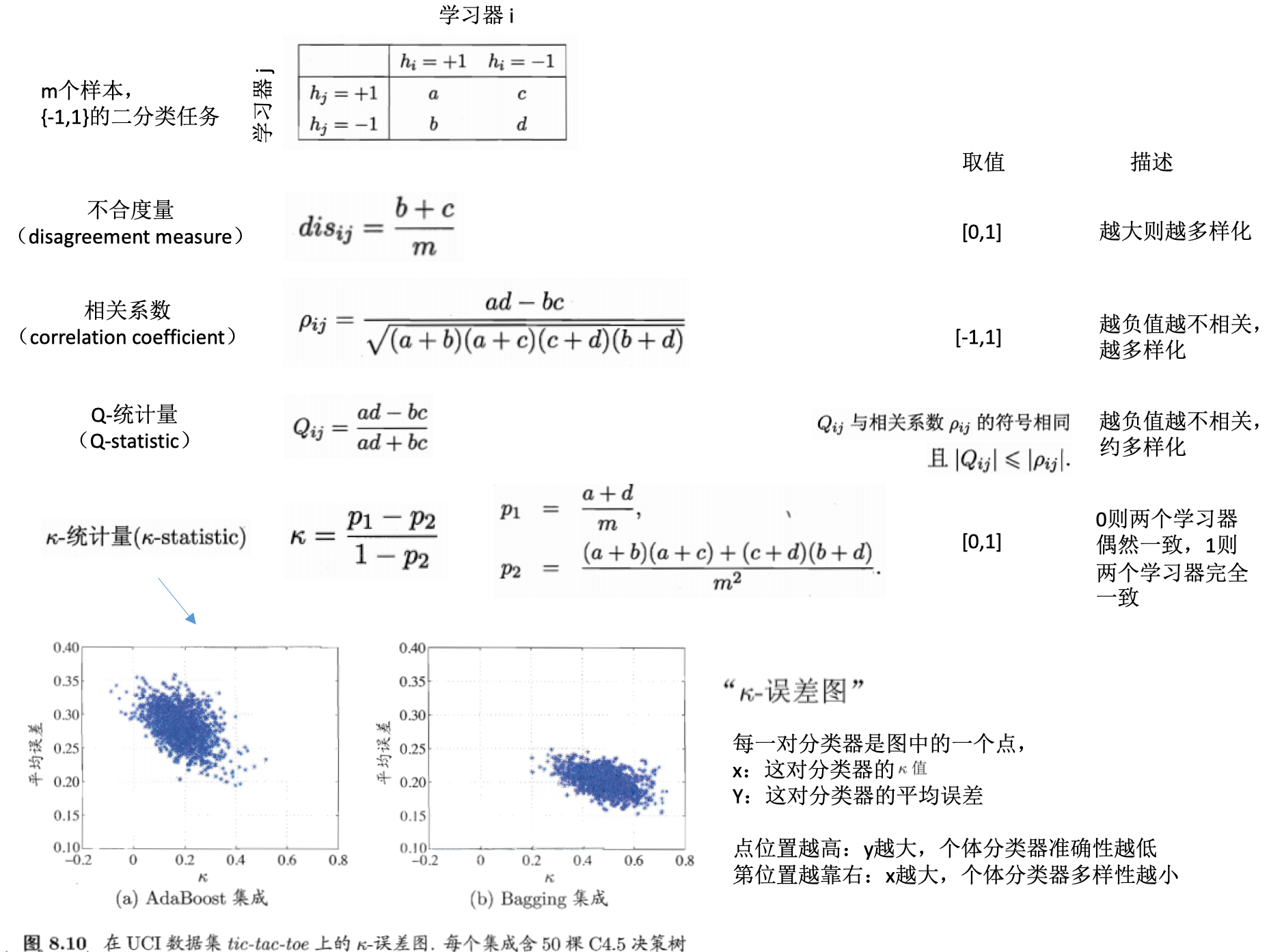
误差-分歧（ambiguity）分解：

• 好：误差大小

• 不同：模型之间的分歧或者单个模型与整体模型的分歧

• 分歧：个体学习器在样本x上的不一致性
• 单个学习器的分歧：\(A(h_i\|x)=(h_i(x)-H(x))^2\)

• 集成学习器的分歧：\(\overline{A}(h\|x)=\sum_{i=1}^Tw_i(h_i\|x)=\sum_{i=1}^Tw_i(h_i(x)-H(x))^2\)

• 误差
• 单个学习器的误差：\(E(h_i\|x)=(f(x)-h_i(x))^2\)

• 集成学习器的误差：\(E(H\|x)=(f(x)-H(x))^2\)

• 个体学习器泛化误差的加权平均：\(\overline{E}=\sum_{i=1}^Tw_iE_i\)
• 个体学习器的加权分歧值：\(\overline{A}=\sum_{i=1}^Tw_iA_i\)
• 集成泛化误差：\(E=\overline{E} - \overline{A}\)
• 个体学习器的准确性越高（上面的\(\overline{E}\)越小）、多样性越大（上面的\(\overline{A}\)越大），则集成越好（上面的\(E\)越小）

学习器多样性的度量

学习器多样性的增强

有不同的方法可以增强学习器的多样性：

• 核心思路：引入随机性
  • 数据样本扰动：采样法
  • 输入属性扰动：不同的子空间提供不同视角，随机子空间算法
  • 输出表示扰动：对输出表示进行操纵，比如变动类标记，或者调制转换等

  • 算法参数扰动：学习算法的参数设置差异

  • 随机森林：使用了数据样本扰动和输入属性扰动

回归：多模型平均比单一模型效果更好的证明

在回归问题中，计算单个模型与真实值的差异，经过换算，可以表示为如下，即单个模型的差距是总的模型的差距，再加一个大于0的项，所以总的模型的差距是更小的：

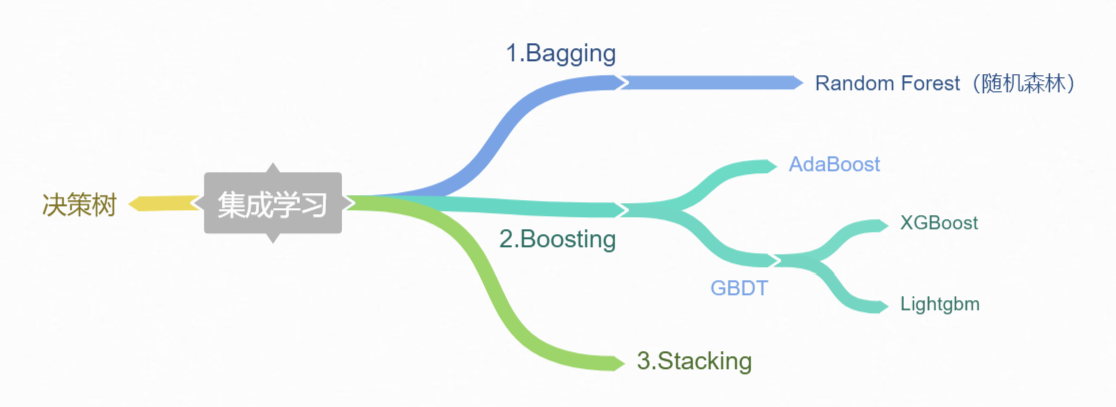
不同类别的集成算法

集成算法（ensemble method）：又叫元算法（meta-algorithm），将不同的分类器组合起来。

• 个体学习器的生成方式进行分类：
  • 串行（序列化方法）：个体学习器间存在强依赖关系。代表：boosting
  • 并行：个体学习器间不存在强依赖关系。代表：bagging，随机森林
• 集成方式进行分类：
  • 集成不同的算法
  • 同一算法在不同设置下的集成
  • 数据集不同部分分配给不同分类器之后的集成

uniform blending：权重相同

• 分类：每个模型权重为1，投票表决
  • 每个\(g_t\)是一样的，此时跟选任意一个\(g_t\)效果一样
  • 每个\(g_t\)有一些差别，投票表决
  • 多分类，票数最多的一类
• 回归：所有的预测值求均值
  • 每个\(g_t\)是一样的，此时跟选任意一个\(g_t\)计算是一样的
  • 每个\(g_t\)有一些差别，求平均能消除不同的模型效果差异很大的情况

linear blending: 权重不同的线性组合

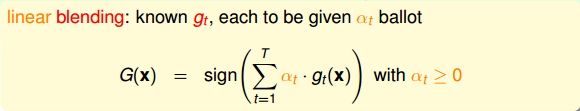
• 每个 g(t)的权重不同
• 如何确定权重？误差最小化思想

stacking(any blending)：非线性组合

• G(t)是g(t)的任意组合：可以是非线性的
• 优点：提高模型复杂度，更好的预测模型
• 缺点：过拟合的危险。采用正则化。

如何得到不同的\(g_t\)

• 如何得到不同的\(g_t\)，以用于模型的融合
• 不同的方法：
  • 选取不同的模型
  • 设置同一模型的不同参数
  • 算法的随机性
  • 选择不同的数据样本

\(g_t\)的结合策略

• 平均法：数值型输出（回归类型）
  • 简单平均：每个学习器认为权重是一样的
  • 加权平均：每个学习器有一个权重
• 投票法（voting）：类别输出（分类任务）
  • 绝对多数投票法：若某标记得票过半数，则预测为该标记；否则拒绝预测。
  • 相对多数投票法：预测为得票最多的标记，若同时多个标记有相同最高票，随机选择一个。

  • 加权投票法：类似加权平均，每个学习器有自己的权重，预测为得票最多的标记，若同时多个标记有相同最高票，随机选择一个。

  • 每个学习器的输出类型
  • 类标记：属于0或1类别，硬投票
  • 类概率：输出某类的概率，软投票
• 学习法
  • 训练数据很多
  • 学习法：通过另一个学习器来进行结合
  • 代表：stacking
  • 初级学习器：个体学习器。相同则是同质的，不同则是异质的。
  • 次级学习器（元学习器）：用于结合的学习器

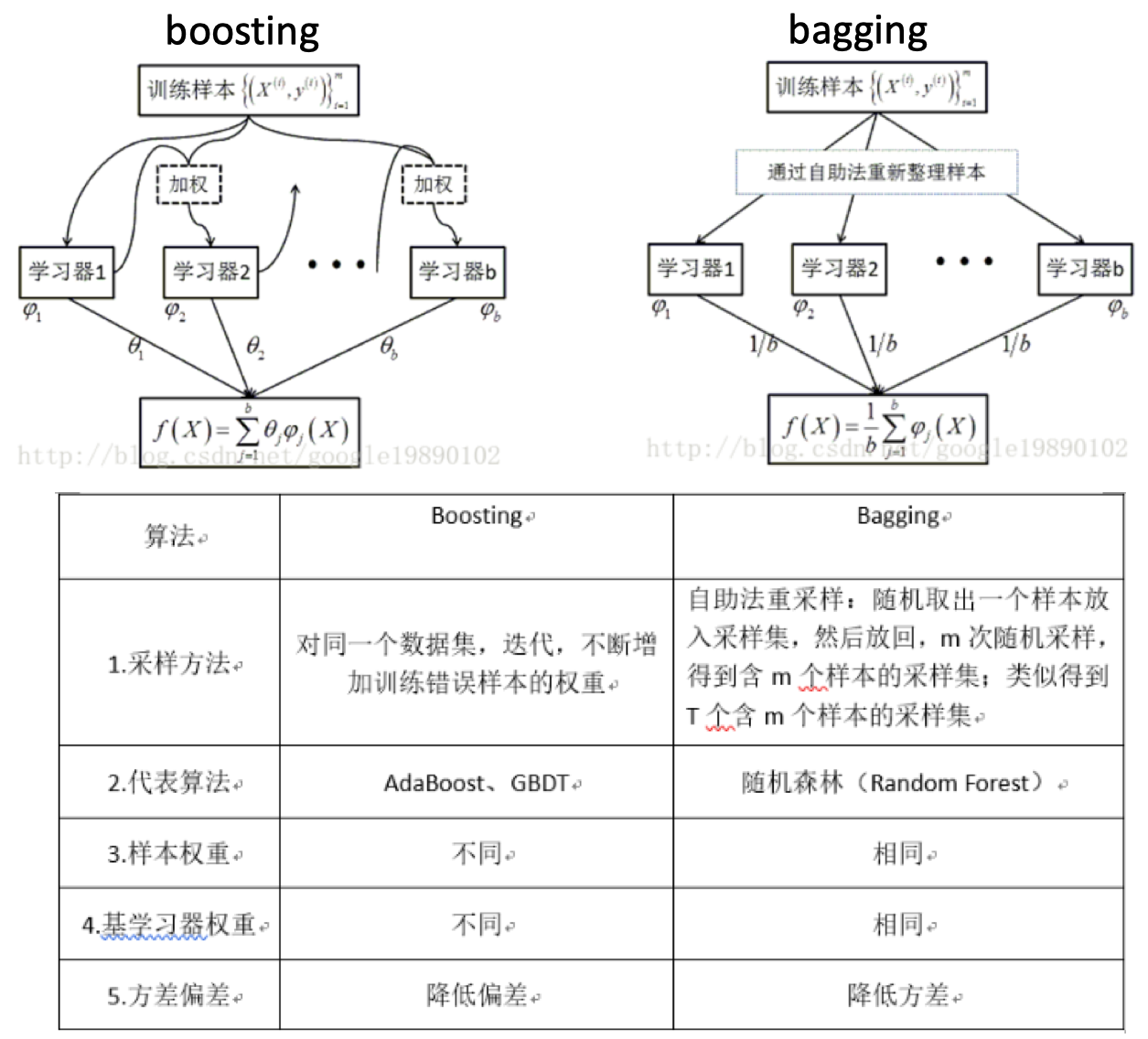
bagging vs random forest vs boosting

1. bagging：
   • 自举汇聚法（Bootstrap aggregating）：从原始数据集选择S次以得到S个数据集。
   • 每个数据集与原数据集大小相等，可以重复抽取。
   • 训练：每个数据集训练一个模型，得到S个分类器模型。
   • 预测：对于新数据，用S个分类器进行分类，然后投票，最多的分类即为最后的分类结果。若分类预测时出现两个类同样的票，最简单的做法是随机选择一个。
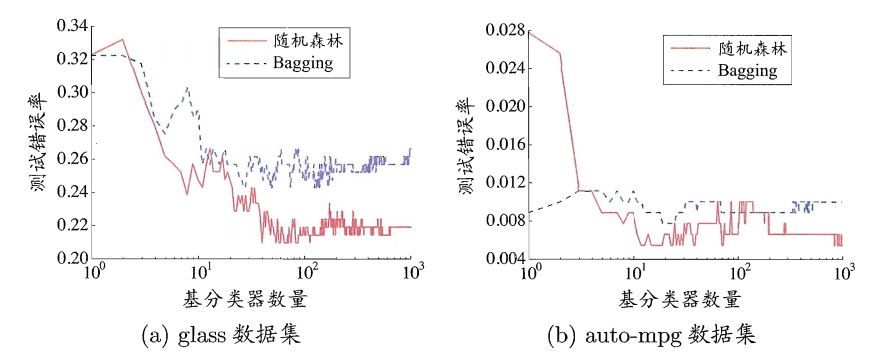
2. bagging vs 随机森林：
   • 随机森林也是一种bagging方法：组合多个决策树。但是在bagging基础上，在决策树的训练中引入了随机属性选择。推荐选择的k值：\(k=log_2d\)，d是属性（特征）数目。
   • 随机森林的收敛性与bagging相似。
   • 起始性能差，因为引入了属性扰动，个体学习器的性能往往会降低。
   • 个体学习器数目增加，会收敛到更低的泛化误差
   • 随机森林的训练效果常常优于bagging：引入了属性选择，相当于考察的子集，而bagging则是全部属性
   • 下图比较的就是两者的泛化能力随着基学习器数目（集成规模）的变化：
3. boosting：
   • 类似于bagging
   • 串行训练，每一个新的分类器都是基于已训练的分类器，尤其关注之前的分类器错误分类的那部分样本数据
   • 所有分类器的加权求和，而bagging中的分类器的权重是相等的。boosting的分类器权重：对应分类器在上一轮中的成功度。
   • AdaBoost（adaptive boosting，自适应boosting）：最流行的一个boosting版本。

AdaBoosting

1. AdaBoosting:
   • 加性模型（additive model）：集学习器的线性组合
   • 问题：使用弱分类器和数据集构建一个强分类器？弱是说模型的效果不太好，比随机好一点。
2. AdaBoosting算法过程：
   • 权重等值初始化：每个训练样本赋值一个权重，构成向量D；
   • 第一次训练：训练一个弱分类器
   • 第二次训练：在同一数据集上进行训练，只是此时的权重会发生改变。降低第一次分类对的样本的权重，增加分类错的权重。样本权重值更新的公式如下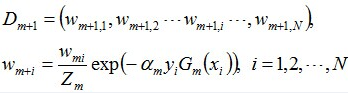：。从这里可以看到，如果某个样本被分错了，则\(y_i * G_m(x_i)\)为负，负负得正，取指数后数值大于1，所以次样本权重值相对上一轮是增大的；如果某个样本被分对了，则\(y_i * G_m(x_i)\)为正，负正得负，取指数后数值小于1，所以次样本权重值相对上一轮是减小的。
   • ……

   • 第n次训练：此时得到的模型是前n-1个模型的权重线性组合。当模型的分类错误率达到指定阈值（一般为0）时，即可停止训练，采用此时的分类器模型。比如3次训练即达到要求的模型最终是：\(G(x)=sign[f_3(x)]=sign[\alpha_1 * G_1(x) + \alpha_2 * G_2(x) + \alpha_3 * G_3(x)]\)

   • 训练得到多个分类器，每个分类器的权重不等，权重值与其错误率相关。
   • 错误率：\(\theta_m = \frac{分类错误的样本数目}{所有样本数目}\)，其中\(m\)是第几次的训练。错误率是每一次训练结束后，此次的分类器的错误率，需要计算，因为这关乎到此分类器在最终的分类器里的权重。
   • 分类器权重：\(\alpha_m = \frac{1}{2} ln(\frac{1-\theta_m}{\theta_m})\)。
3. AdaBoosting算法示例：
   • 这里以一个10个样本的数据集（每个样本1个特征），详细的解释了如何训练AdoBoost算法，及每一轮迭代中阈值的选取，样本权重值的更新，分类器错误率的计算，分类器权重值的计算等过程，可以参考。
4. AdaBoosting算法损失函数：
   • 这里的\(\theta_m\)就是分类器的权重值（即上面的\(\alpha_m\)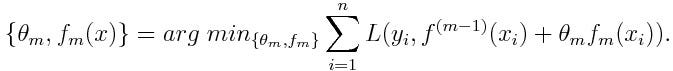）。要求解使得该函数最小化，可以采用前向分步算法（forward stagewise）策略：从前向后，每一步只学习一个基函数及其系数。

AdaBoost：Python源码版本

构建多个单层决策树的例子，比如对于一组数据样本（包含两个类别），具有两个特征，如何区分开来？

• stumpClassify：对于样本指定的特征，基于一个阈值，对样本进行分类，比如高于这个阈值的设置为-1（取决于判断符号threshIneq ）
• buildStump：对于样本、类别、权重D，构建一个多决策树。对样本的每一个特征进行查看，在每一个特征的取值范围内不断的尝试不同的阈值进行分类，同时不停的更新权重矩阵D，最终的目的是找到使得分类错误率最小时的特征、特征阈值、判断符号（大于还是小于，为啥这个会有影响？）。

def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
    retArray = ones((shape(dataMatrix)[0],1))
    if threshIneq == 'lt':
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0
    return retArray
    
def buildStump(dataArr,classLabels,D):
    dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
    m,n = shape(dataMatrix)
    numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
    minError = inf #init error sum, to +infinity
    for i in range(n):#loop over all dimensions
        rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
        stepSize = (rangeMax-rangeMin)/numSteps
        for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
            for inequal in ['lt', 'gt']: #go over less than and greater than
                threshVal = (rangeMin + float(j) * stepSize)
                predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
                errArr = mat(ones((m,1)))
                errArr[predictedVals == labelMat] = 0
                weightedError = D.T*errArr  #calc total error multiplied by D
                #print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
                if weightedError < minError:
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst

AdaBoost：sklearn版本

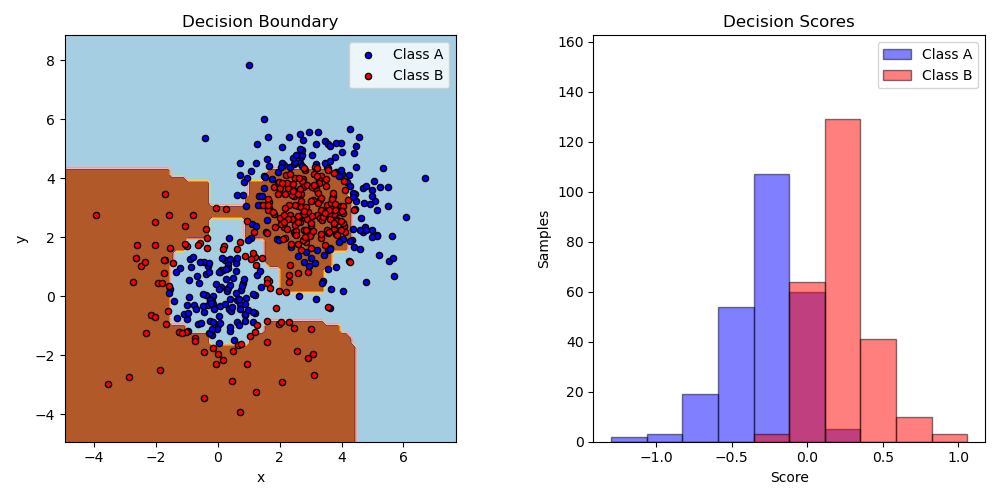
sklearn给出了一个二分类的例子，首先生成了一个数据集，两个高斯分布混合而成的。这些样本是线性不可分的，使用AdaBoost算法，构建基于决策树的分类器，可以很好的区分开来：

import numpy as np
import matplotlib.pyplot as plt

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_gaussian_quantiles


# Construct dataset
X1, y1 = make_gaussian_quantiles(cov=2.,
                                 n_samples=200, n_features=2,
                                 n_classes=2, random_state=1)
X2, y2 = make_gaussian_quantiles(mean=(3, 3), cov=1.5,
                                 n_samples=300, n_features=2,
                                 n_classes=2, random_state=1)
X = np.concatenate((X1, X2))
y = np.concatenate((y1, - y2 + 1))

# Create and fit an AdaBoosted decision tree
bdt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1),
                         algorithm="SAMME",
                         n_estimators=200)

bdt.fit(X, y)

plot_colors = "br"
plot_step = 0.02
class_names = "AB"

plt.figure(figsize=(10, 5))

# Plot the decision boundaries
plt.subplot(121)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
                     np.arange(y_min, y_max, plot_step))

Z = bdt.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
plt.axis("tight")

# Plot the training points
for i, n, c in zip(range(2), class_names, plot_colors):
    idx = np.where(y == i)
    plt.scatter(X[idx, 0], X[idx, 1],
                c=c, cmap=plt.cm.Paired,
                s=20, edgecolor='k',
                label="Class %s" % n)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.legend(loc='upper right')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Decision Boundary')

参考

• 机器学习实战第7章
• 机器学习周志华第8章
• 决策树、GBDT、XGBoost和LightGBM之GBDT
• Adaboost 算法的原理与推导
• Boosting algorithm: AdaBoost