目录
神经元模型
- 神经网络：由具有适应性的简单单元组成的广泛并行互联的网络，它的组织能够模拟生物神经系统对真实世界所做出的交互反应。【Kohonen，1988】
- 基本成员：神经元模型
- 兴奋时，会向其他相连的神经元发送化学物质，而改变这些神经元的电位。
- 如果某神经元的电位超过了一个阈值，那么就被激活，处于兴奋状态，向其他神经元发送化学物质。
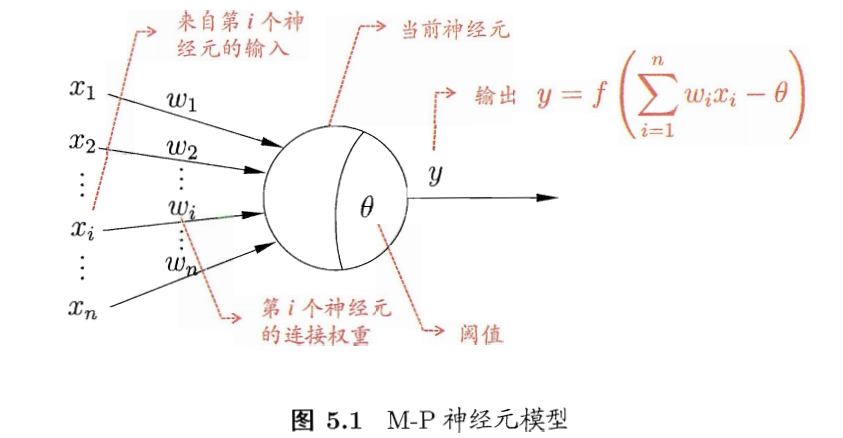
- M-P神经元模型：
- 1943，McCulloch and Pitts
- 神经元接收来自n个其他神经元的输入信号，通过带权重的链接进行传递，收到的总输入值与神经元的阈值相比，然后通过激活函数处理以产生输出
- 激活函数
- 理想的：阶跃函数，将信号输出为1（兴奋）或者0（抑制）
- 阶跃函数：不连续，不光滑
- 实际使用Sigmoid函数，将输入值挤压到(0,1)，也称挤压函数。
感知机与多层网络
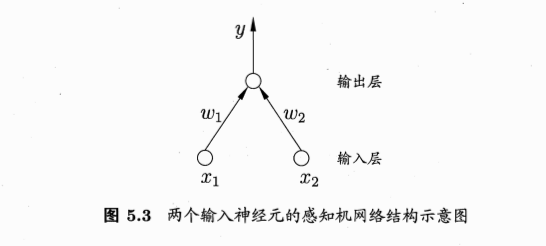
感知机
- perceptron，两层神经元组成
- 输出层是M-P神经元（阈值逻辑单元）
感知机的线性组合：aggregation
- 把许多感知机线性组合起来
- 得到的G也是一个感知机模型
- 包含两层权重：输入层到隐藏层的权重\(w_t\)，隐藏层到输出层的权重\(\alpha\)
- 包含两层sign函数：注意是两层，隐藏层的转换有一层，最后输出层的转换也有一层
线性组合的感知机可实现非线性边界计算
- 例子：两个感知机线性组合实现逻辑AND运算
- g1,g2取值为{-1,1}
- G(x) = sign(-1 + g1(x) + g2(x))
- g1=-1，g2=-1，则G(x)=0
- g1=-1，g2=1，则G(x)=0
- g1=1，g2=-1，则G(x)=0
- g1=1，g2=1，则G(x)=1
- 所以只有当g1和g2均取正值1时，组合的G才取正值1
感知机越多越好？
- 感知机的线性组合同样很powerful
- 比如感知机越多时，可以得到更加光滑的分隔边界和稳定的模型
- 使用的感知机越多，能得到任意的convex set（凸多边形边界）
- 越多时模型越复杂，也容易过拟合
多层功能神经元: multi-layer
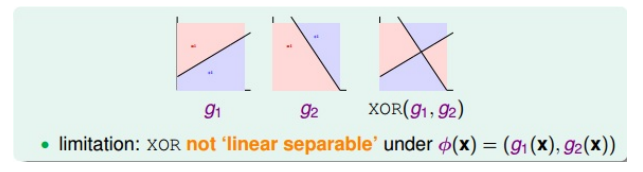
单层感知机线性组合的局限：
- 能实现一些非线性问题：比如AND、OR、NOT
- 有的非线性问题不能解决，比如：实现异或(XOR)操作。为什么不能解决？因为XOR得到的是非线性可分的区域。
单层扩展到多层，解决异或问题
- XOR的拆分：\(XOR(g_1,g_2) = OR(AND(-g_1, g_2), AND(g_1, -g_2))\)
- 拆分的结果显示，本身异或操作就是两次转换：第一层的AND，第二层的OR
- 对应的感知机模型：
多层神经网络：
- 感知机：简单
- 感知机的线性组合aggregation：powerful，能解决部分非线性问题
- 多层前馈神经网络(multi-layer feedforward neural networks)：more powerful
输出层：
- 输出的是一个分数
- 可选择不同的线性模型
- 二分类：linear classification模型
- 线性回归问题：线性回归模型
- 软分类问题：逻辑回归模型
中间层：
- 中间层，每层有神经元
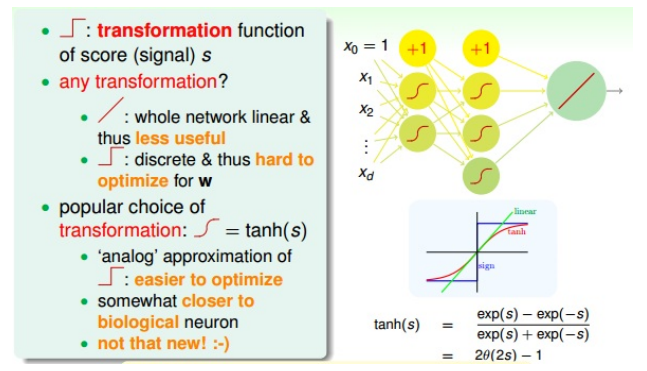
- 不使用线性函数做变化。如果每个神经元（节点）都是进行线性运算，那么通过线性组合的神经网络模型也必然是线性的。这跟直接使用一个线性模型没有区别。
- 不使用阶梯函数(sign，非线性)做变换：离散、不处处可导，在优化计算时难处理
- 常使用tanh(s)做变换：\(tanh(s) = \frac{exp(s)-exp(-s)}{exp(s)+exp(-s)}\)
- 平滑函数，类似”S“型
- 当|s|较大时，tanh(s)与阶梯函数相近
- 当|s|较小时，tanh(s)与线性函数相近
- 处处可导，便于优化计算
- 形状类似阶梯函数，具有非线性性质
- 与sigmoid逻辑函数关系：\(tanh(s)=2\theta(2s) - 1, \theta(s)=\frac{1}{1+exp(s)}\)
感知机和网络的学习
- 给定训练数据集，权重\(w_i(i=1,2,...,n)\)，基于阈值\(\theta\)可通过学习得到
- 阈值\(\theta\)可看做一个固定输入为-1的哑结点（dummy node）所对应的链接权重\(w_{n+1}\)，=》权重和阈值的学习统一为权重的学习
- 学习过程，就是根据训练数据来调整神经元之间的连接院(connection weight)以及每个功能神经元的阈值。（连接权重+阈值 =》统一的权重）
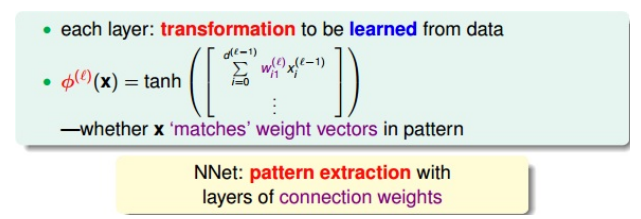
- 学习的核心：pattern extraction，模式提取
- 例子：以tanh作为激活函数为例
- 神经网络的学习：
- 计算的过程是转换：输入的x和权重w的乘积
- 乘积越大，则tanh(wx)越接近于1，表明这种转换的效果越好。
- w、x为两个向量，乘积越大，则两向量的內积也越大，两向量越接近于平行，表明x和w有模式上的相似性。
- 如果每一层的输入x和权重w有模式的相似性，比较接近平行，那么转换的效果越好，能够得到表现良好的神经网络模型
- 核心：模式提取，从数据中找到数据本身蕴含的模式和规律
误差逆传播算法:BP
- BP算法（error backpropagation）：神经网络的学习算法
- BP网络：
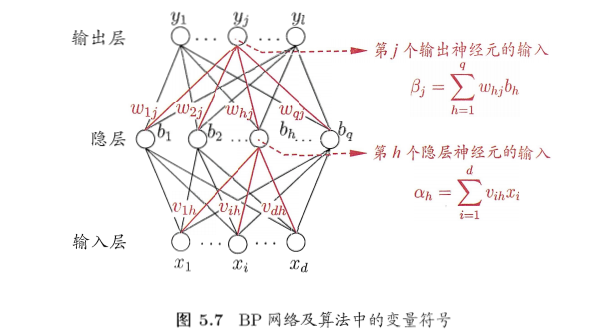
- 参数数目：(d+l+1)q+l，
- 输入层到隐藏层的权重：dxq
- 隐藏层到输出层的权重：qxl
- 隐藏层神经元的阈值：q
- 输出层神经元的阈值：l
- 基于梯度下降策略，以目标的负梯度方向对参数进行调整
- BP流程：
神经网络的过拟合优化
- 如果是SGD：每次迭代更新时只取一个点，会不够稳定。可采用mini-batch的方式，每次选取一些数据，训练然后求平均值更新权重
- 容易过拟合：训练误差持续下降，测试误差上升
- 缓解策略1：早停(early stopping)，若训练集误差降低，验证集误差升高，则停止训练。使用验证集进行迭代次数的选取。
- 缓解策略2：正则化，目标函数增加一个描述网络复杂度的部分，比如链接权重和阈值的平方和。
- 熟悉的是L2正则化：\(\Omega=\sum (w_{ij}^{(l)})^2\)，但是使得每个权重进行等比例缩小(shrink)，大的权重缩小程度大，小的权重缩小程度小，问题：难以得到值为0的权重，而这时我们希望的，如果某些权重为0，则权重是稀疏的，能减少VC demension。
- L1正则化：\(\sum \|w_{ij}^{(l)}\|\)，权重的稀疏解。但是绝对值不容易微分。
- 常用的weighted-elimination regularizer：\(\sum \frac{(w_{ij}^{(l)})^2}{1+(w_{ij}^{(l)})^2}\)，类似于L2，但是做了尺度的缩小，能使得大的权重和小的权重得到同等程度的缩小，从而让更多的权重为0。
全局最小与局部极小
- 若\(E\)表示神经网络在训练集上的误差，则它是关于连接权重\(w\)和阈值\(\theta\)的函数。参数寻优过程，在参数空间中，寻找一组最优参数使得E最小。
- 最优：
- 局部极小：local minimum，参数空间中的某个点，邻域点的误差均大于此点。梯度为0的点，只要其附近的点的误差大于此点，则此点为局部极小。
- 局部极小可有多个，全局最小只有一个。
- 全局最小：global minimum，参数空间的所有点的误差均大于此点
- 全局最小一定是局部最小，反之不成立。
- 如果有多个局部最小，则不能保证找到的解是全局最小 =》陷入局部最小。
- 跳出局部最小的策略
- 多组不同参数初始化。多个不同的初始点开始搜索，取最小的，可能不陷入局部最小。
- 模拟退化技术。在每一步都以一定的概率接受比当前解更差的结果，从而有助于跳出局部最小。
- 随机梯度下降。不同于标准的梯度下降，随机梯度下降在计算梯度时引入随机因素，有机会跳出局部最小。
- 遗传算法。训练神经玩过更好的逼近全局最小。
其他常见神经网络
RBF网络
- RBF(Radial Basis Function): 径向基函数网络
- 单隐藏层前馈神经网络
- 使用径向基函数作为隐藏层神经元的激活函数
- 输出层是对隐藏层输出的线性组合
- RBF网络表示：\(\phi(x)=\sum_{i=1}^qw_i\rho(x, c_i)\)，q隐藏层神经元个数，\(c_i\)第i个神经元对应的中心，\(w_i\)第i个神经元对应的权重
- 训练步骤：
- 1.确定神经元中心\(c_i\)，随机采用、聚类等方式
- 2.利用BP算法确定参数\(w_i,\beta_i\)
ART网络
- 竞争型学习：无监督学习策略，输出神经元相互竞争，每一时刻仅有一个竞争获胜的神经元被激活，其他均处于抑制状态（胜者通吃原则：winner-take-all）
- ART(adaptive resonance theory)：自适应谐振理论网络。
- 比较层：接收输入样本，传给识别神经元
- 识别层：神经元对应一个模式类
- 识别阈值
- 重置模块
- 可进行增量学习或在线学习
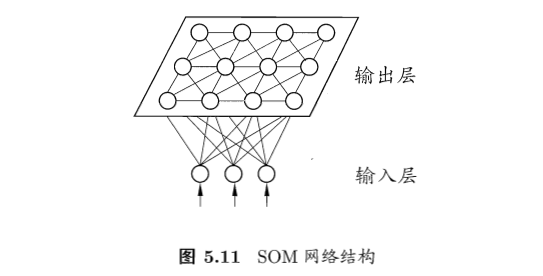
SOM网络
- SOM(self-organizing map)：自组织映射网络
- 竞争学习型的无监督神经网络
- 将高维数据映射到低维空间，同时保持高维空间的拓扑结构，即高维空间相似的样本点映射到网络输出层中的邻近神经元
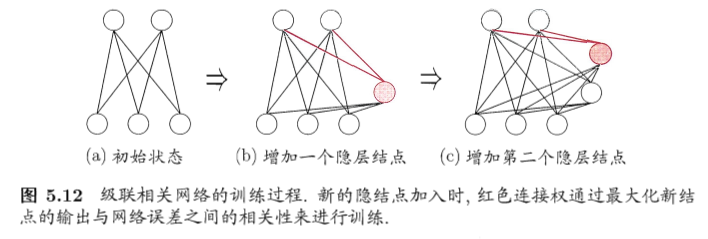
自适应网络：级联相关网络
- 结构自适应网络：网络结构也是学习的目标之一
- 在训练过程中找到最符合数据特点的网络结构
- 代表：级联相关网络（cascade-correlation）
- 级联：建立层次链接的层级结构，随着训练，会建立新的层级
- 相关：通过最大化新神经元的输出与网络误差之间的相关性来训练相关的参数
- 优点：
- 无需设置网络层数、隐藏神经元数目
- 训练速度快
- 缺点：
- 数据小时容易过拟合
RNN：Elman网络
- 递归神经网络：网络中可出现环状结构
- 最早的递归神经网络：Elman网络
Boltzmann机
- 能量：为网络状态定义一个能量，最小化时网络最理想，网络训练就是最小化此能量函数
- 基于能量的模型：玻尔兹曼机
- 显层：数据的输入和输出
- 隐层：数据的内在表达
- 神经元都是布尔型，0、1两种状态，1是激活，0是抑制
参考
- 机器学习周志华第5章
- 林轩田机器学习技法课程学习笔记12 — Neural Network
If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/neural-network.html
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me