期望、方差、协方差、相关系数
2017-07-11
期望
- 定义:实验中每次可能结果的概率乘以其结果的总和
- 反映随机变量平均取值的大小
- 线性运算:\(E(ax+by+c)=aE(x)+bE(y)+c\)
- 推广形式:\(E(\sum_{k=1}^{n} a_i x_i + c) = \sum_{k=1}^{n}(a_i E(x_i)) + c\)
- 函数期望:
- f(x)是x的函数
- 离散函数:\(E(f(x))=\sum_{k=1}^{n}f(x_k)P(x_k)\)
- 连续函数:\(E(f(x))=\int_{-\infty}^{\infty}f(x)p(x)dx\)
- 性质:
- 函数的期望大于期望的函数,即\(E(f(x)) >= f(E(x))\)
- 一般情况下,乘积的期望不等于期望的乘积
- 如果X和Y相互独立,则\(E(xy)=E(x)E(y)\)
方差
- 度量随机变量和其数学希望之间的偏离程度
- 是一种特殊的期望
- 定义:\(Var(x)=E((x-(E(x))^2))\)
- 性质:
- 变种:\(Var(x)=E(x^2)-(E(x))^2\)
- 常数的方差为0
- 方差不满足线性性质
- 如果X和Y相互独立,则\(Var(ax+by)=a^2Var(x)+b^2Var(y)\)
import numpy as np
arr = [1,2,3,4,5,6]
#求均值
arr_mean = np.mean(arr)
#求方差
arr_var = np.var(arr)
#求标准差
arr_std = np.std(arr,ddof=1)
print("平均值为:%f" % arr_mean)
print("方差为:%f" % arr_var)
print("标准差为:%f" % arr_std)
协方差
- 衡量两个变量线性相关性强度及变量尺度
- 定义:\(Cov(x,y)=E((x-E(x))(y-E(y)))\)
- 方差是一种特殊的协方差:
- 当X=Y时,\(Cov(x,y)=Var(x)=Var(y)\)
- 性质:
- 两个独立变量的协方差为0。因为此时独立的随机变量x、y满足:\(E[xy]=E(x)E(y)\)
- 计算公式:\(Cov(\sum_{i=1}^{m}a_{i}x_{i}, \sum_{j=1}^{m}b_{i}y_{i})=\sum_{i=1}^{m}\sum_{j=1}^{m}a_{i}b_{j}Cov(x_{i}y_{i})\)
- 特殊情况:\(Cov(a+bx,c+dy)=bdCov(x,y)\)
- 理解:
- 表示的是两个变量总体误差的期望
- 如果两个变量的趋势一致,比如变量x大于自身期望且y也大于自身期望,那么两个变量x、y之间的协方差就是正值
- 如果两个变量的趋势相反,比如变量x大于自身期望但是y小于自身期望,那么两个变量x、y之间的协方差就是负值
from numpy import array
from numpy import cov
x = array([1,2,3,4,5,6,7,8,9])
print(x)
y = array([9,8,7,6,5,4,3,2,1])
print(y)
Sigma = cov(x,y)[0,1]
print(Sigma)
# [1 2 3 4 5 6 7 8 9]
# [9 8 7 6 5 4 3 2 1]
# -7.5
相关系数
- 研究两个变量之间线性相关程度的量
- 为什么引入相关系数?
- 协方差就是描述两个变量X、Y的相关程度的
- 相同量纲下,协方差没有问题
- 但是当x、y属于不同量纲时,协方差会在数值上表现出很大的差异
- 因而引入了相关系数
- 定义:\(Corr(x,y)=\frac{Cov(x,y)}{\sqrt({Var(x)Var(y)})}\)
- 性质:
- 取值范围在[-1, 1],可看成无量纲的协方差
- 值越接近于1,正相关性越强;越接近于-1,负相关性越强;等于0时,没有相关性。
from scipy import stats
# two sample rank test
def sig_spearman_corr(x,y):
p=stats.spearmanr(x,y)[0]
return p
def sig_pearson_corr(x,y):
p=stats.pearsonr(x,y)[0]
return p
参考
Read full-text »
Sequencing adapter: mode and trimming
2017-04-29
Read full-text »
LATEX常见用法
2017-04-26
LATEX常见用法
这里也总结了一些常见的写法,可以参考一下:
Greek letters
| Symbol | Script |
|---|---|
| \(\alpha\) | \alpha |
| \(\beta\) | \beta |
| \(\theta\) | \theta |
| \(\pi\) | \pi |
Power and indices
| Symbol | Script |
|---|---|
| \(k_{n+1}\) | k_{n+1} |
| \(n^2\) | n^2 |
| \(k_n^2\) | k_n^2 |
| \(k_{n^2}\) | k_{n^2} |
Fractions and Binomials
| Symbol | Script |
|---|---|
| \(\frac{n!}{k!(n-k)!}\) | \frac{n!}{k!(n-k)!} |
| \(\binom{n}{k}\) | \binom{n}{k} |
| \(\frac{\frac{x}{1}}{x - y}\) | \frac{\frac{x}{1}}{x - y} |
| \(^3/_7\) | ^3/_7 |
Roots
| Symbol | Script |
|---|---|
| \(\sqrt{k}\) | \sqrt{k} |
| \(\sum_{\substack{0<i<m,0<j<n}} P(i, j)\) | \sum_{\substack{0<i<m,0<j<n}} P(i, j) |
Sums and Integrals
| Symbol | Script |
|---|---|
| \(\sum_{i=1}^{10} t_i\) | \sum_{i=1}^{10} t_i |
| \(\sqrt[n]{k}\) | \sqrt[n]{k} |
| \(\sum_{i=1}^{m}\sum_{j=1}^{m}\) | \sum_{i=1}^{m}\sum_{j=1}^{m} |
Some other constructions
| Symbol | Script |
|---|---|
| \(\overline{abc}\) | \overline{abc} |
| \(\overline{abc} \\ a_i\) | \overline{abc} \\\ a_i,两个斜杠\\表示分行 |
| \(\cdot\),\(\cdot\cdot\cdot\) | \cdot,\cdot\cdot\cdot,位于中心的点 |
| \(\bigoplus\) | \bigoplus |
| \(\leftarrow\), \(\rightarrow\) | \leftarrow, \rightarrow |
| \(\longleftarrow\), \(\longrightarrow\) | \longleftarrow, \longrightarrow,长的版本 |
| \(\wedge\) | \wedge,可表示并且,逻辑字符 |
| \(w^{[l]}=\begin{bmatrix}1.5 & 0 \\0 & 1.5\end{bmatrix}\) | w^{[l]}=\begin{bmatrix}1.5 & 0\\0 & 1.5\end{bmatrix},矩阵表示 |
| \(w^{[l]}=\begin{matrix}1.5 & 0 \\0 & 1.5\end{matrix}\) | w^{[l]}=\begin{matrix}1.5 & 0\\0 & 1.5\end{matrix},矩阵表示 |
| \(w^{[l]}=\begin{pmatrix}1.5 & 0 \\0 & 1.5\end{pmatrix}\) | w^{[l]}=\begin{pmatrix}1.5 & 0\\0 & 1.5\end{pmatrix},矩阵表示 |
| \(\mid x \mid\) | \mid x \mid |
| \(\int_{-\infty}^{\infty}\) | \int_{-\infty}^{\infty} |
参考
Read full-text »
Venn plot
2017-04-19
推荐2个online版本的venn工具,画出来的图是很漂亮的:
- http://bioinfogp.cnb.csic.es/tools/venny_old/index.html 最多画4个集合的;
-
http://bioinfogp.cnb.csic.es/tools/venny/ 这是上面的工具的2.0版本,可以用这个;

Read full-text »
Normalization
2017-04-18
归一化
定义:将数据缩放到特定的区间中,以使得数值之间具有可比较性。
目标:
- 把数变为[0, 1]之间的数值
- 有量纲表达式变为无量纲表达式
为什么需要归一化:
- 提升模型的收敛速度。在梯度下降时,如果不同的特征的值范围差异很大,那么达到全局最小所需的步数就会很多。
- 提升模型的精度。比如在计算相似性(距离等)时,不同数值范围的特征对距离值所产生的影响是不一样的(小的特征值可能不怎么影响),当进行归一化之后,能够使得不同的特征做出的贡献相同。
- 防止梯度爆炸。在神经网络中,梯度爆炸就是由于初始化权值过大,前面层会比后面层变化的更快,就会导致权值越来越大,梯度爆炸的现象就发生了。
哪些模型需要归一化:
- SVM:在特征缩放后,最优解与原来的不等价,所以如果不做缩放,模型参数会被较大或者较小的参数所主导。
- 逻辑回归:在特征缩放后,不会改变最优解,但是如果目标函数过于不均一,收敛会很慢,所以需要归一化。
- 神经网络、SGD:模型效果会强烈的依赖于归一化
哪些模型不需要归一化:
- 特征值在【0,1】之间的不再需要,否则会破坏其原始的稀疏性
- 决策树:效果不受归一化影响
- ICA:不需要归一化
- 最小二乘法OLS:不需要
方法
1. min-max normalization (Rescaling)
公式:\(X_{norm} = \frac{X - X_{min}}{X_{max}-X_{min}}\)
结果:将原始数据经过线性变换,把数值缩放到[0,1]之间,不会改变数据的分布。
2. Mean normalization
公式:\(X_{norm} = \frac{X - X_{mean}}{X_{max}-X_{min}}\)
结果:将原始数据经过线性变换,把数值缩放到[-1,1]之间
3. Standardization (标准化),z-score标准化,zero-mean normalization
公式:\(X_{norm} = \frac{X - X_{mean}}{\sigma}\),其中\(\sigma\)是标准差。
结果:转换后的数值,其平均值为0,方差为1,即服从标准正太分布,这个转换不会改变数据的分布。
4. Scaling to unit length
公式:\(X_{norm} = \frac{X}{\|X\|}\),其中\(\|X\|\)是这个数据向量的欧式长度(Euclidean length)。
结果:转换后的数值在[0,1]之间。
5. log函数转换
公式:\(X_{norm} = \frac{log{X}}{log{X_{max}}}\)
结果:转换后的数值在[0,1]之间。
6. atan函数转换
公式:\(X_{norm} = atan{X}*\frac{2}{\pi}\)
结果:如果X都大于0,则区间映射到[0,1],小于0的数据映射到[-1,0]之间。
7. quantile normalization
原理:
- 1)记录每个样本(列)中的每个数据的rank(原始rank);
- 2)每个样本,从小到达排序,计算排序后每个rank的平均值(排序后rank平均值);
- 3)根据原始rank从排序后rank平均值提取对应的值,取代原来的值,即为归一化之后的值。

结果:使得不同的数据集具有相同的分布,容易比较。(这个方法在microarray数据中使用得很多,原先叫quantile standardization,后来才叫做quantile normalization。wiki给出了一个例子,说的是在不同的样本中,如果将基因的表达量归一化到同一水平。)。下面是不同样本中前后表达量分布的例子: 
例子比较
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('ticks')
np.random.random(42)
X = np.random.exponential(size=1000)
X_norm_min_max = (X - X.min()) / (X.max() - X.min())
X_norm_mean_max = (X - X.mean()) / (X.max() - X.min())
X_norm_zscore = (X - X.mean()) / X.std()
X_norm_unit = X / np.linalg.norm(X)
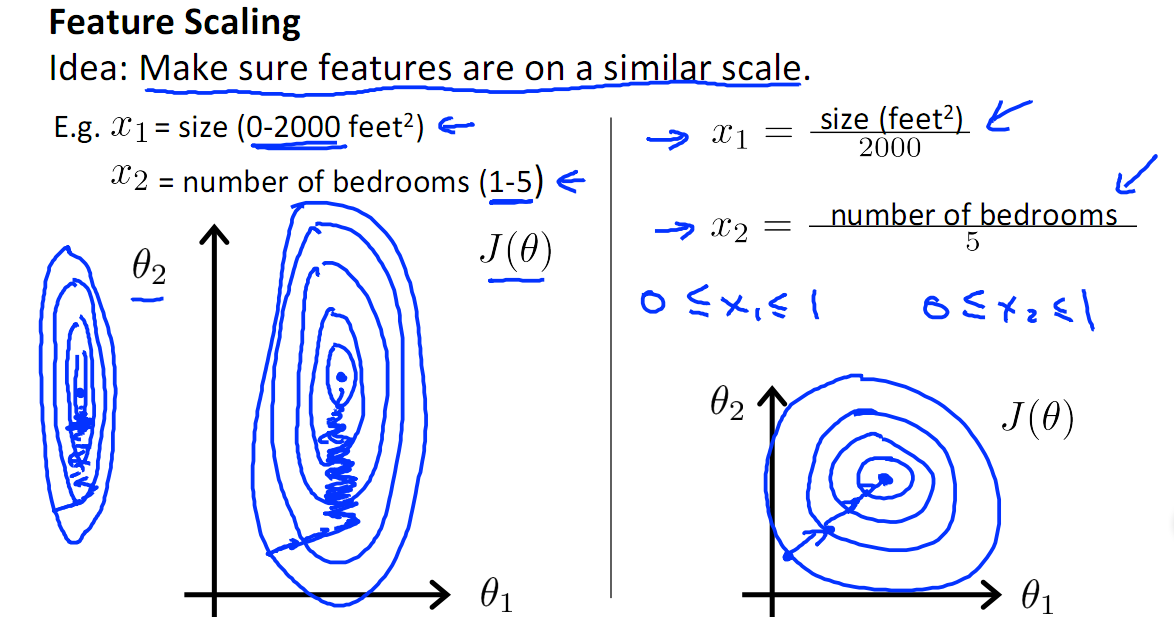
fig, ax = plt.subplots(3, 2, figsize=(16,18), sharex=False, sharey=False)
sns.distplot(X, ax=ax[0,0])
ax[0,0].set_title('Raw')
sns.distplot(X_norm_min_max, ax=ax[0,1])
ax[0,1].set_title('min-max norm')
sns.distplot(X_norm_mean_max, ax=ax[1,0])
ax[1,0].set_title('mean-max norm')
sns.distplot(X_norm_zscore, ax=ax[1,1])
ax[1,1].set_title('z-score norm')
sns.distplot(X_norm_unit, ax=ax[2,0])
ax[2,0].set_title('unit length norm')
参考
- Feature_scaling @ wiki
- 数据标准化/归一化normalization
- 标准化和归一化什么区别?
- About Feature Scaling and Normalization
- Preprocessing data@sklearn
- Quantile_normalization @ wiki
Read full-text »
Violin plot
2017-04-05
plot use sns.violinplot
# violin plot
def df_sns_violinplot(df,col_str,savefn,orient='v',class_col="",order=None):
assert savefn.endswith("png"), "[savefn error] should be .png: %s"%(savefn)
savefn=savefn.replace('png','violin.png')
print "[df_sns_violinplot]"
col_str = None if col_str == "" else col_str
class_col= None if class_col == "" else class_col
print " - col_str: %s"%(col_str)
print " - class_col: %s"%(class_col)
print df.head(2)
print df.dtypes
#fig,ax=plt.subplots(nrows=1,ncols=1,figsize=(8,8)) # plot multiple violin in one fig
if class_col:
s=sns.violinplot(y=col_str,x=class_col,data=df,order=order) # ax=ax[0,1,...]
else:
print "plot col_str: ",col_str
#s=sns.violinplot(x='p_val_poisson',data=df) # ax=ax[0,1,...]
s=sns.violinplot(df[col_str],order=order) # ax=ax[0,1,...]
title_str=savefn.split("/")[-1]+':'+str(df.shape[0])
fig=s.get_figure()
fig.suptitle(title_str)
fig.savefig(savefn)
print " - savefig: %s"%(savefn)
plt.close()
return savefn
Read full-text »
Tmux: 终端复用
2017-03-18
会话嵌套
在本地使用tmux打开了会话,在会话中登陆了服务器,然后打开了服务器上的tmux会话。如果本地和服务器上对于快捷键的设置是一样的,那么输入快捷键时只能被外部的会话捕捉到。可以通过对快捷键字母输入两次的方式将命令传入到内层的会话,比如:
Ctl + b + <: 是在外部跳到左边的panelCtl + b + b + <: 是在内部跳到左边的panel。(字母输入两次)
更新config文件
有时候想修改config设置,比如不同的快捷键等,可以按照如下步骤:
- 修改文件:~/.tmux.conf。现在使用的文件可在这里下载到,同时使用``和
Ctl+b作为前置键。 - 进入tmux终端
- 敲击
: source-file ~/.tmux.conf或者tmux source ~/.tmux.conf - 可参考的tmux配置: oh-my-tmux。这个里面可以把前后的window修改一下,默认屏蔽掉了
n,p选择前后tab的功能. - 在tmux里面,可以
前置键+r直接reload修改后的tmux配置
Read full-text »
Python module numpy
2017-03-02
python numpy
Read full-text »
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me