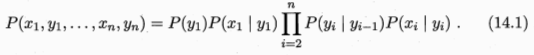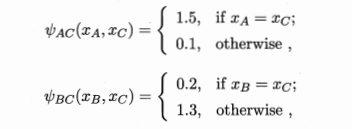Home > MachineLearning > Main text

概率图模型

Tag: python, machine learning
2019-01-07

目录

图模型

  • 任务：根据已观测的样本对感兴趣的未知变量进行估计和推测
  • 概率模型：将学习任务归结为计算变量的概率分布的描述框架
    • 推断：利用已知变量推测未知变量的分布。核心：基于观测变量推测出未知变量的条件分布。
    • 给定：关心的变量集合Y、可观测变量集合O、其他变量集合R
    • 生成式模型：考虑联合分布\(P(Y,R,O)\)
    • 判别式模型：考虑条件分布\(P(Y,R\|O)\)
    • 推断：由观测变量值\(P(Y,R,O)\)或者\(P(Y,R\|O)\)，推断得到条件概率分布\(P(Y\|O)\)
  • 概率图模型：
    • 一类用图表达变量相关关系的概率模型
    • 节点：一个或一组随机变量
    • 边：变量间的概率相关关系（变量关系图）
  • 分类：基于边的性质
    • 有向图（贝叶斯网）：使用有向无环图表示变量间的依赖关系
    • 无向图（马尔科夫网）：使用无向图表示变量间的相关关系

隐马尔科夫模型（有向图）

  • 隐马尔科夫模型：hidden markov model，HMM
    • 结构最简单的动态贝叶斯网络
    • 著名的有向图模型
    • 时序数据建模：语音识别、自然语言处理
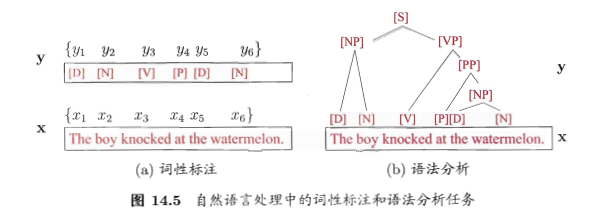
  • 变量：
    • 状态变量：\(y_i\)，第i时刻的系统状态，通常为隐藏的，也称为隐变量(hidden variable)
    • 系统通常在多个状态之间切换，因此状态变量的取值范围称为状态空间，通常是N个可能取值的离散空间。
    • 观测变量：\(x_i\)，第i时刻的观测值
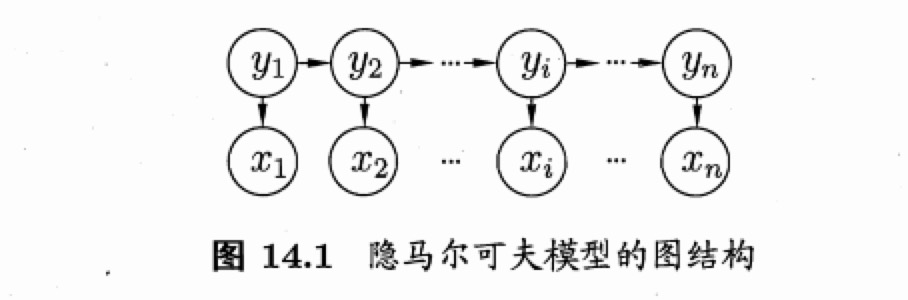
  • 箭头：变量间的依赖关系
  • 观测变量：取值仅依赖于状态变量，即\(x_t\)由\(y_t\)确定，与其他状态变量及观测变量的取值无关
  • t时刻的状态\(y_t\)仅依赖于t-1时刻的状态\(y_{t-1}\)，与其余n-2个状态无关。即马尔科夫链：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态。
    • 所有变量的联合概率分布：20190815145333
  • 模型参数：
    • 状态转移概率：模型在各个状态间切换的概率。记为矩阵：\(A=[a_{ij}]_{N\times N}\)，其中的\(a_{ij}=P(y_{t+1}=s_j\|y_t=s_i), 1\le i, j\le N\)表示：在时刻\(t\)状态为\(s_i\)，在下一时刻状态为\(s_j\)的概率
    • 输出观测概率：模型根据当前状态获得各个观测值的概率。记为矩阵\(B=[b_{ij}]_{n\times M}\)，其中的\(b_{ij}=P(x_t=o_j\|y_t=s_i), 1\le i, j\le N\)表示：在时刻\(t\)状态为\(s_i\)，则观测值为\(o_j\)的概率
    • 初始状态概率：模型在初始时刻各状态出现的概率。记为\(\pi={\pi_1,\pi_2,...,\pi_N}\)，其中\(\pi_i=P(y_1=s_i), 1\le i\le N\)表示：模型的初始状态为\(s_i\)的概率
  • 模型表示：
    • 状态空间Y
    • 观测空间\(\chi\)
    • 3参数：状态转移概率，输出观测概率，初始状态概率，\(\lambda=[A,B,\pi]\)
  • 对于给定参数的模型，产生观测序列的过程：
    • 设置t=1,根据初始状态概率\(\pi\)选择初始状态\(y_1\)
    • 根据状态\(y_t\)和输出观测概率\(B\)选择观测变量取值\(x_t\)
    • 根据状态\(y_t\)和状态转移矩阵\(A\)转移模型状态，即确定\(y_{t+1}\)
    • 若\(t<n\),设置\(t=t+1\)，并转移到第2步，否则停止
  • 3个基本问题：
    • 给定模型与观测序列的匹配程度。给定模型\(\lambda=[A,B,\pi]\)，如何计算产生观测序列\(x=[x_1,x_2,...,x_n]\)的概率\(P(x\|\lambda)\)。【根据以往的观测，推测当前观测有可能的值，求取概率\(P(x\|\lambda)\)取最大的】
    • 给定模型和观测推断隐藏状态。给定模型\(\lambda=[A,B,\pi]\)和观测序列\(x=[x_1,x_2,...,x_n]\)，如何找到与此观测序列最匹配的状态序列\(y={y_1,y_2,...,y_n}\)。【语音识别：观测值为语音信号，隐藏状态为文字，根据信号推测最可能的文字】
    • 给定观测序列得到最佳模型参数。给定观测序列\(x=[x_1,x_2,...,x_n]\)，如何调整模型参数\(\lambda=[A,B,\pi]\)，使得该序列出现的概率最大。【通常不好人工指定模型参数，需根据训练样本学得最优参数】

马尔科夫随机场（无向图）

  • 典型的马尔科夫网的无向图模型
  • 节点：一个或一组变量
  • 边：变量之间的依赖关系

  • 势函数（potential functions）:又称为因子，定义在变量子集上的非负实函数，主要用于定义概率分布函数

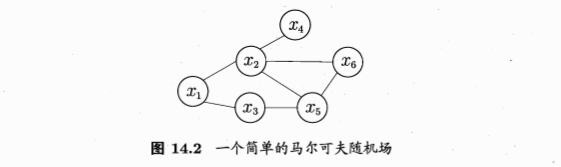
  • 例子：简单的随机场 20190815153007
  • 团：clique，对于某个子集节点，若其中任意两结点有边连接，则子集为一个团
  • 极大团：maximal clique，在一个团中加入另外任何一个结点都不再形成团。极大团就是不能被其他团所包含的团。
  • {x1,x2,x3}不构成团，因为x2与x3之间无连接
  • {x2,x6}是团，但不是极大团，因为可加入x5，从而形成团。同样的{x2,x5},{x5,x6}都不是极大团
  • 极大团：{x1,x2},{x1,x3},{x2,x4},{x3,x5},{x2,x5,x6}

  • 每个节点至少出现在一个极大团中

  • 多变量的联合概率分布：
    • 基于团分解为多个因子的乘积，每个因子仅与一个团有关
    • n个变量\(x={x_1,x_2,...,x_n}\)，所有团构成的集合是C，\(x_Q\)：团\(Q\subset C\)对应的变量集合

    • 联合概率：\(P(x)=\frac{1}{Z}\prod_{Q\subset C}\phi_Q(x_Q)\)，\(\phi_Q\)是团Q对应的势函数（因子），可对Q中的变量关系进行建模，Z是规范化因子，确保P(x)是被正确定义的概率。

    • 若变量个数很多，团数目很多，很多项的乘积，有计算负担
    • 注意：若团Q不是极大团，则Q必须被一个极大团\(Q'\)包含，即\(x_Q\subseteq x_{Q*}\)
    • 所以联合概率可基于极大团定义
    • 极大团集合为\(C'\)：\(P(x)=\frac{1}{Z*}\prod_{Q\subset C*}\phi_Q(x_Q)\)
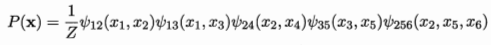
    • 对于上面的例子有(5个极大团的联合)：20190815154733
  • 条件独立性
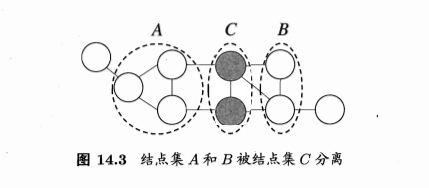
    • 从结点集A的结点到B的结点都必须经过结点集C，则A和B被C分离，C称为分离集 20190815155320
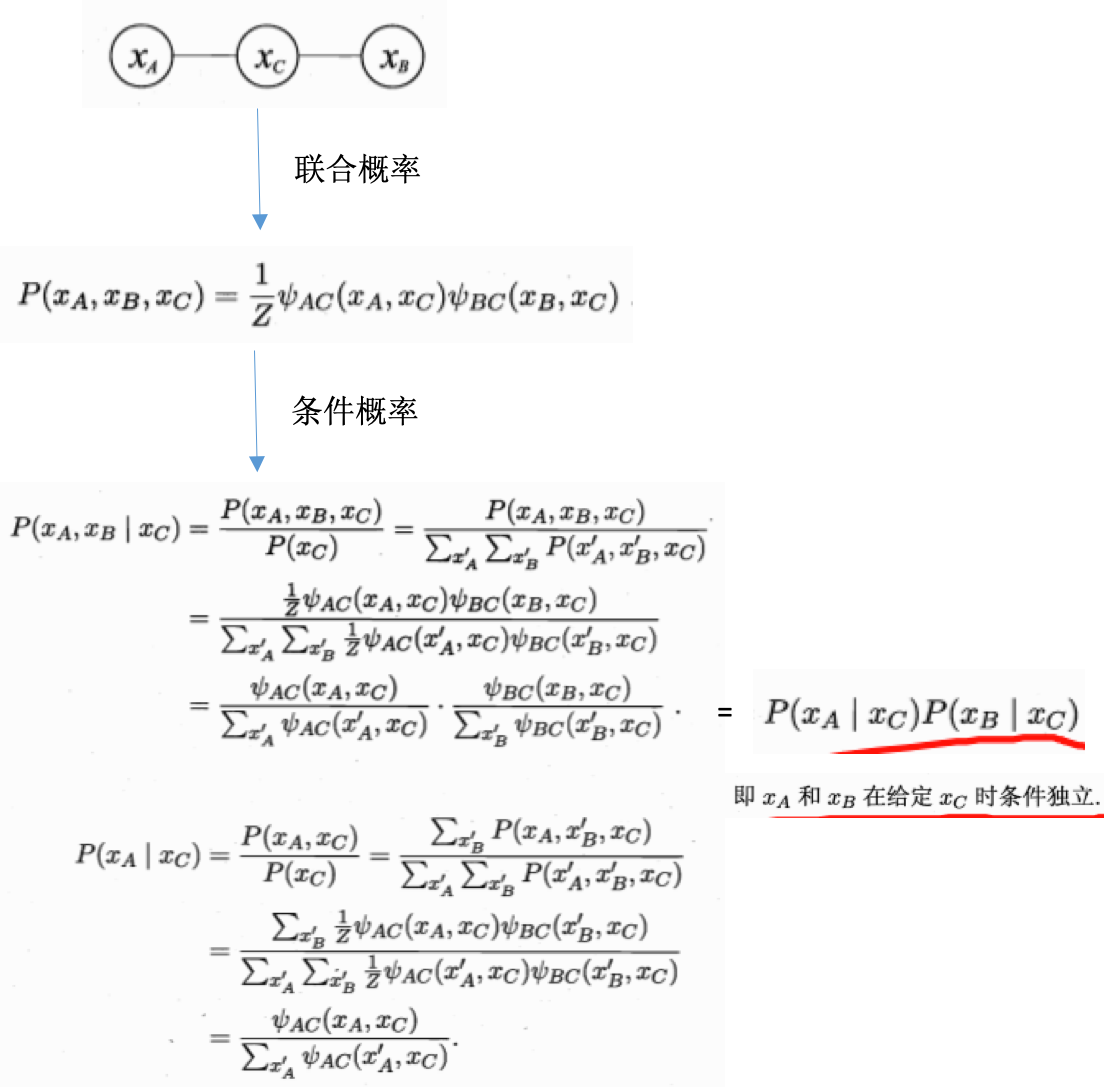
    • 全局马尔科夫性：给定两个变量子集的分离集，则这两个变量子集条件独立 20190815155817
    • 【推论】局部马尔科夫性：给定某变量的邻接变量，则该变量条件独立于其他变量
    • 【推论】成对马尔科夫性：给定所有其他变量，两个非邻接变量条件独立
  • 势函数：
    • 定量刻画变量集\(x_Q\)中变量之间的相关关系
    • 非负函数：指数函数通常用于定义势函数，\(\phi_Q(x_Q)=e^{-H_Q(x_Q)}\)
    • 在所编号的变量取值上有较大函数值
    • 例子：20190815160226
    • 该模型偏好A、C取相同值（势能大），B、C取不同值（势能小）
    • 即：A、C正相关，B、C负相关
    • 联合概率：如果A、C相同，B、C不同，则联合下来将取得较高的联合概率

条件随机场

  • 生成式模型：对联合分布进行建模。隐马尔科夫模型、马尔科夫随机场都是生成式的。
  • 判别式模型：对条件分布进行建模。条件随机场模型。
  • 条件随机场：
    • 判别式模型
    • 无向图
    • 对多个变量在给定观测值后的条件概率进行建模
    • 观测序列：\(x={x_1,x_2,...,x_n}\)
    • 标记序列：\(y={y_1,y_2,...,y_n}\)
    • 目标：构建条件概率，\(P(y\|x)\)
    • 标记变量y可以是结构型变量：分量之间具有某种相关性 20190815162635
    • 词性标注任务：观测为语句，标记为词性，具有线性序列结构
    • 语法分析任务：观测为语句，标记为语法树，具有树形结构
  • \(G=<V,E>\)：结点与标记变量一一对应的无向图，若每个变量\(y_v\)均满足马尔科夫性，即：\(P(y_v\|x,y_{V\{v\}})=P(y_v\|x,y_{n(v)})\)，则(y,x)构成一个条件随机场。
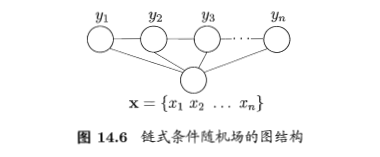
  • 链式条件随机场：chain-structured CRF
    • 最常用的
    • 尤其是标记序列建模时 20190815163628
  • 条件概率定义：
    • 使用势函数+图结构 20190815164655

学习与推断

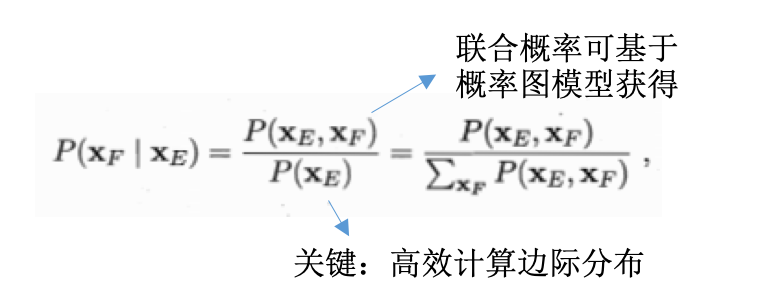
  • 基于概率图模型定义的联合概率分布，对目标变量的边际分布或以某些可观测变量为条件的条件分布进行推断
  • 边际分布：对无关变量求和或者积分后得到的结果。
    • 例子：马尔科夫网，变量的联合分布表示为极大团的势函数乘积，给定参数\(\Theta\)求解变量x的分布，就是对其他无关变量进行积分的过程，称为边际化（marginalization）
  • 参数估计（学习）：确定具体分布的参数，极大似然法估计或者最大后验概率估计求解
  • 具体的：
    • 变量集x：分为不相交的\(x_E, x_F\)
    • 推断目标：计算边际概率\(P(x_F)\)或者条件概率\(P(x_F\|x_E)\): 20190815165847
  • 概率图推断：
    • 精确推断：计算出目标变量的边际分布或条件分布的精确值。一般计算复杂度极高。
    • 近似推断法：在较低的时间复杂度下获得原问题的近似解。

变量消去（精确推断）

  • 动态规划算法
  • 利用图模型所描述的条件独立性来消减计算目标概率值所需的计算量

  • 最直观的精确推断法

  • 有向图的推断流程：20190815171256

  • 同样适用于无向图

  • 缺点：
    • 若需计算多个边际分布，重复使用变量消去法将会造成大量的冗余计算

信念传播

  • 信念传播：belief propagation，将变量消去法中的求和操作看做一个消息传递过程，解决多个边际分布计算时的重复问题
    • 消去过程看成是消息传递过程
    • 每次消息传递仅与变量xi及其邻接结点直接相关（消息传递的计算被限制在图的局部进行）
    • 一个结点仅在接收到其他所有结点的消息后才能向另一个结点发送消息
    • 结点的边际分布正比于所接收的消息的乘积

近似推断

  • 精确推断：大计算开销
  • 近似推断：更常用
    • 采样：sampling，使用随机化方法完成近似
    • 变分推断：variational inference，使用确定性近似完成近似推断

MCMC采样

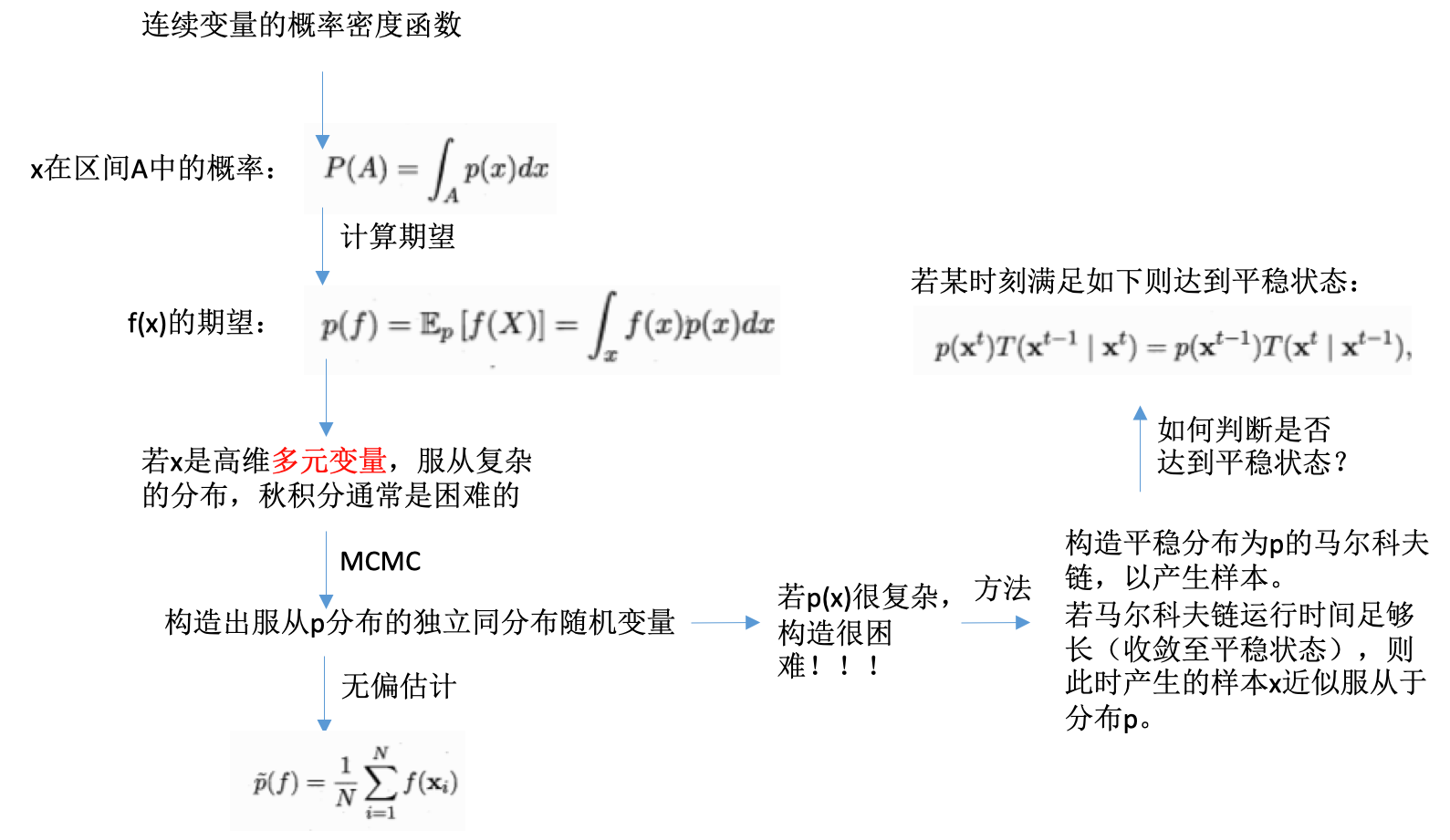
  • 关心分布不是真的关心分布，是可以计算期望，以提供决策
  • 推断很可能是计算期望
  • 如果直接计算期望比推断概率更容易，则可直接操作计算期望使得推断的求解更高效
  • 例子：20190815172817

  • 关键：采样，高效的基于图模型所描述的概率分布来获取样本

  • MCMC：
    • 马尔科夫链蒙特卡洛方法
    • markov chain monte carlo
    • 概率图模型最常用的采样技术
  • 具体：
    • 构造一条马尔科夫链
    • 马尔科夫链收敛至平稳分布【关键】
    • 此时恰为待估计参数的后验分布
    • 通过这条马尔科夫链来产生符合后验分布的样本
    • 基于生成的样本进行估计 20190815194525
  • 构建马尔科夫链关键：
    • 构造转移概率
    • 不同的构造方法得到不同的MCMC算法
  • MH算法
    • MCMC的代表
    • Metropolis-Hastings
    • 基于拒绝采样来逼近平稳分布p
    • 即每次根据上一轮的采样结果\(x^{t-1}\)来采样获得候选状态样本\(x*\)，但是这个候选样本会以一定的概率被拒绝掉
    • 从状态\(x^{t-1}\)到状态\(x*\)的转移概率为：\(Q(x*\|x^{t-1})A(x*\|x^{t-1})\)，其中\(Q(x*\|x^{t-1})\)是用户给定的先验概率，\(A(x*\|x^{t-1})\)是\(x*\)被接受的概率
    • 若\(x*\)收敛至平稳状态：20190815203512
  • 吉布斯采样：
    • gibbs sampling
    • MH算法的特例
    • 同样适用马尔科夫链获取样本，该马尔科夫链的平稳分布也是采样的目标分布p(x)
    • 具体：
    • 给定\(x={x_1,x_2,...,x_N}\)，目标分布p(x)，初始化x的取值
    • (1) 随机或以某个次序选取某变量\(x_i\)
    • (2) 根据x中除了\(x_i\)外的变量的现有取值，计算条件概率\(p(x_i\|X_{\bar i})\)
    • (3) 根据\(p(x_i\|X_{\bar i})\)对样本变量\(x_i\)采用，用采样值代替原值。【所以区别是没有拒绝概率这一条？】

变分推断

  • 使用已知简单分布来逼近需推断的复杂分布

  • 通过限制近似分布的类型，得到一种局部最优、但具有确定解的近似后验分布

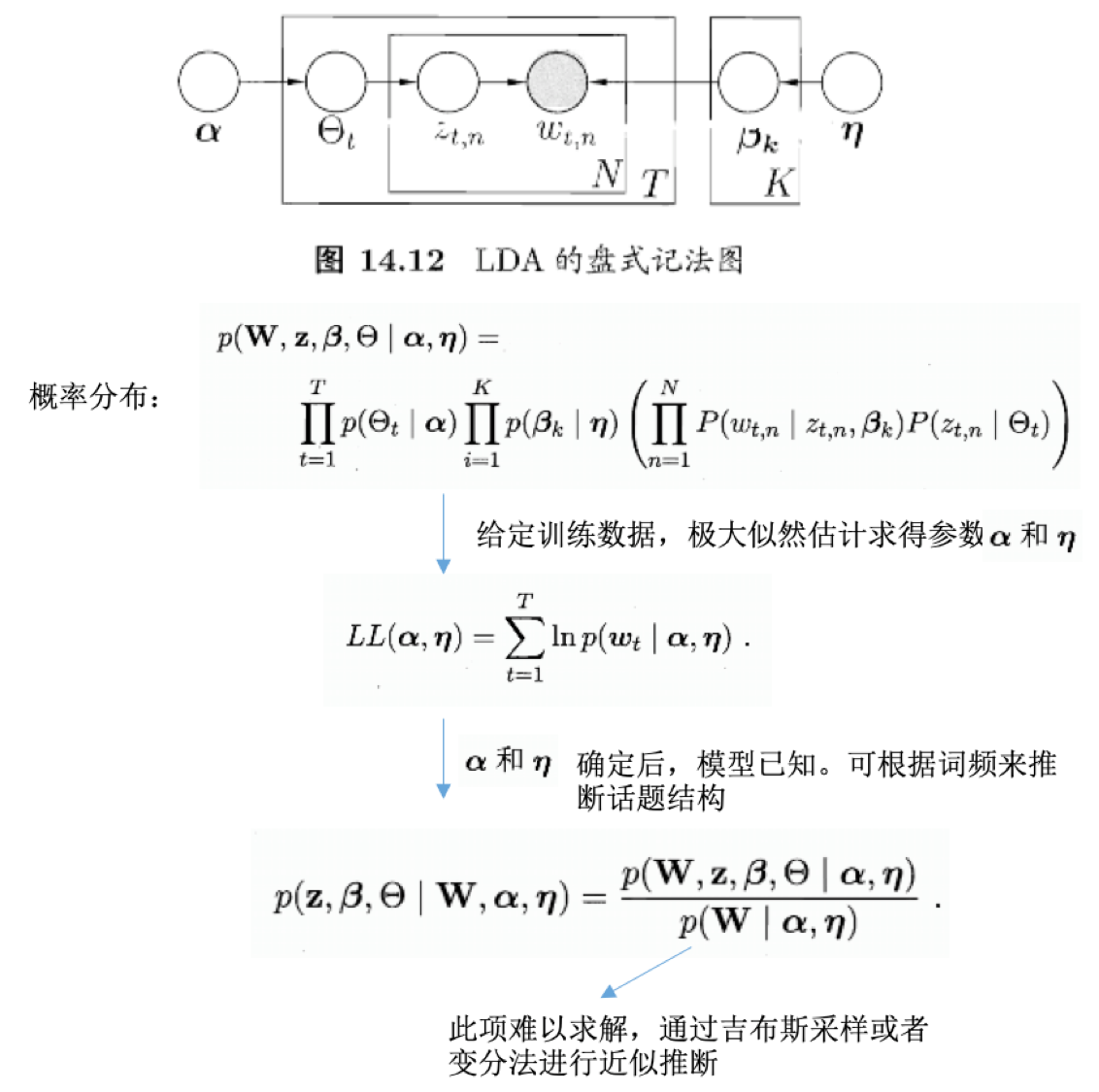
  • 盘式记法：
    • plate notation
    • 概率图模型的一种简洁表示方法
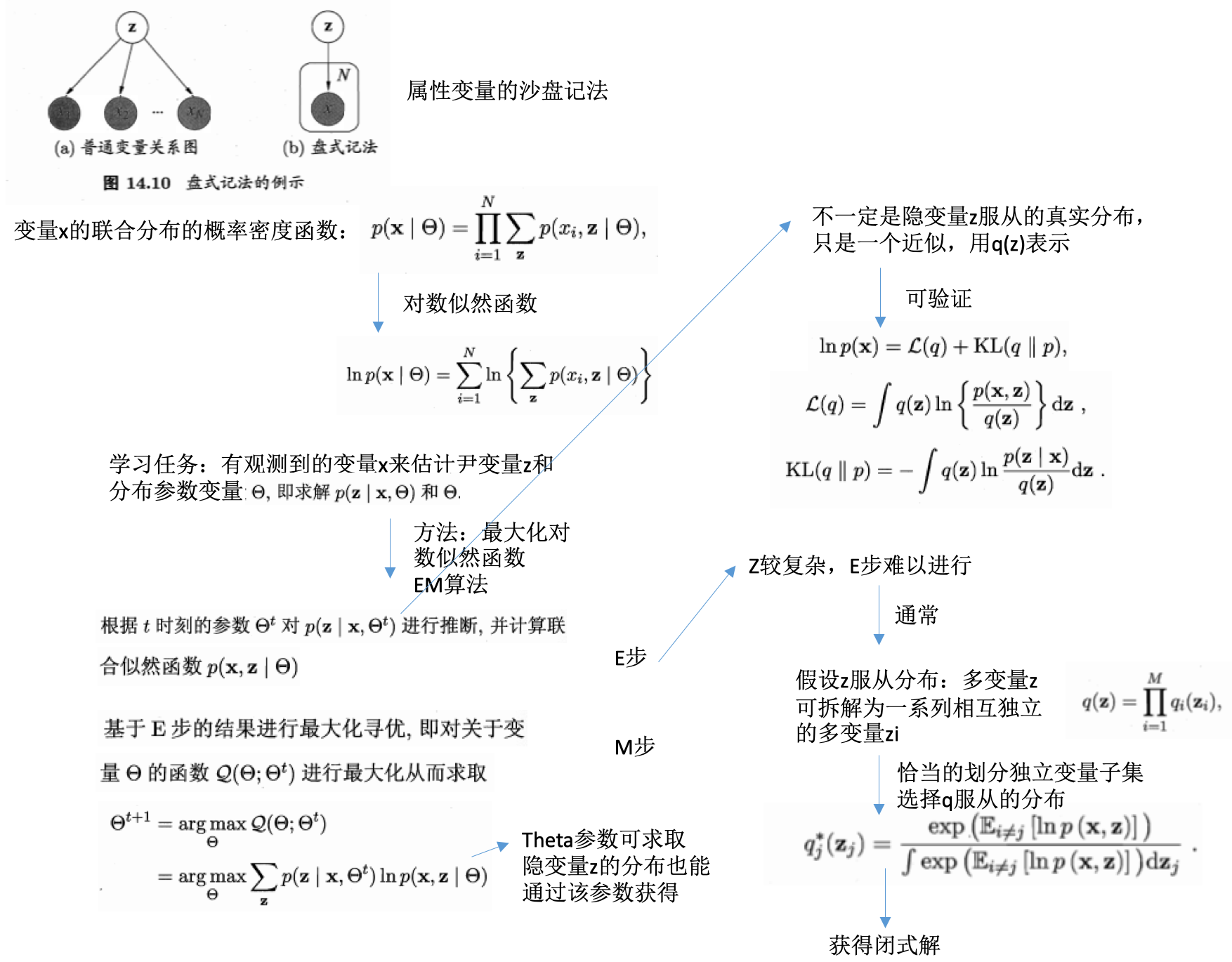
  • 隐变量分解及假设分布：20190815211906
  • 关键：
    • 如何对隐变量进行拆解
    • 假设各变量子集服从何种分布
    • 两者确定后，即可套用上式的结论，结合EM算法进行概率图模型的推断和参数估计
    • 若果隐变量的拆解或分布假设不恰当，会导致效率低、效果差

话题模型

  • 话题模型：
    • 一族生成式有向图模型
    • 处理离散的数据，文本集合、信息检索、自然语言处理
    • 隐狄利克雷分配模型LDA：典型代表，latent dirichlet allocation
  • 词：
    • word
    • 待处理数据的基本离散单元
    • 文本处理：一个词就是一个英文单词
  • 文档：
    • document
    • 待处理的数据对象
    • 由一组词组成
    • 词在文档中不计顺序
    • 一篇文章、网页等
  • 话题：
    • topic
    • 表示一个概念
    • 具体表示为一系列相关的词，以及他们在该概念下出现的概率
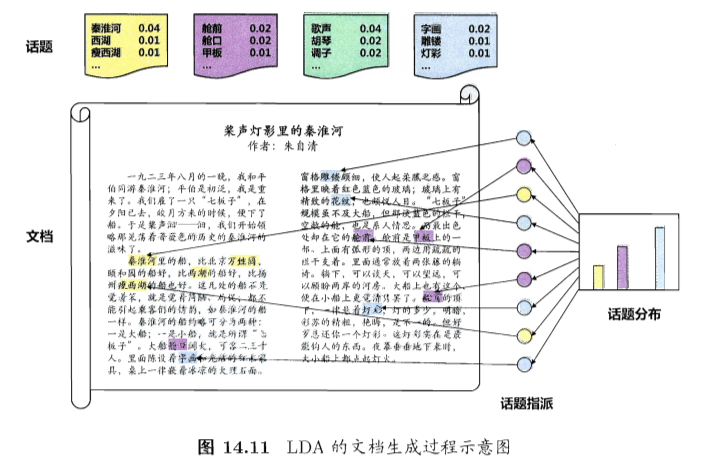
  • LDA生成过程：20190815212815
  • 现实任务：
    • 统计可获得词频向量，但是不知道谈论哪些话题，不知道每篇文档与哪些话题有关
  • LDA：
    • 生成式模型的角度看待文档和话题
    • 每篇文档包含多个话题：\(\Theta_{t,k}\)表示文档t中包含话题k的比例，进而通过下面的步骤由话题生成文档t:
    • 根据参数为\(\alpha\)的狄利克雷分布随机采样一个话题分布\(\Theta_t\)
    • 按如下步骤生成文档中的N个词：
      • 根据\(\Theta_t\)进行话题指派，得到文档t中词n的话题\(z_{t,n}\)
      • 根据指派的话题所对应的词频分布\(\beta_k\)随机采样生成词
  • 示例：这个post举了一个例子，在python中如何进行LDA分析，这里是重新跑的notebook：
    • 目标：分析1987-2016年间发表在NIPS上的文章的文本内容（共6560篇文档），获取话题

    • 工具：sklearn（CountVectorizer统计文本、LatentDirichletAllocation进行LDA分析），pyLDAvis模块进行话题结果的可视化

    • 问题：
    • 【1】文本的前期处理不够干净，比如通过词云图，很多无用的符号（et,al,ie,example）是没有去掉的。当然，最后提取的话题的靠前的term也不包含这些。
    • 【2】执行的速度有点慢
    • 【3】这里直接指定的话题数目是5，没有采用评估量作为依据进行挑选（说会在后续的post给出）
    • 【4】如何基于话题结果对每篇文章assign类型？
    • 【5】跑出来的结果不太一样，比如其topic 0是：”model learning network neural figure time state networks using image “，但我这里是”learning data algorithm function set training problem 10 error kernel“。随机数的设定。

参考

  • 机器学习周志华第14章

If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/probabilistic-graphic-model.html
Previous: Softmax function

    Category

    Latest articles

    Links