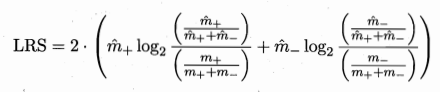目录

• 目录
• 基本概念
• 序貫覆盖
• 剪枝优化
• 一阶规则学习
• 归纳逻辑程序设计
  • 最小一般泛化
  • 逆归结
• 参考

基本概念

• 规则：
  • rule
  • 语义明确、能描述数据分布所隐含的客观规律或领域概念
  • 可写成”若。。。，则。。。“形式的逻辑规则
  • 形式表示：\(\bigoplus \leftarrow f_1 \wedge f_2 \wedge \cdot\cdot\cdot \wedge f_L\)
  • \(\leftarrow\)：逻辑蕴含符号
  • \(f_1 \wedge f_2 \wedge \cdot\cdot\cdot \wedge f_L\)：规则体（body），表示该规则的前提（右边部分）。由逻辑文字组成的合取式，\(\wedge\)：表示并且。
  • \(\bigoplus\)：规则头（head），表示该条规则的结果。一般是逻辑文字，规则所判定的目标类别或概念。
  • \(L\)：规则中逻辑文字的个数，是规则的长度
  • 这样的逻辑规则也称为”if-then规则“
• 规则学习：
  • rule learning
  • 从训练数据中学习出一组能用于对未见示例进行判别的规则
  • 具有更好的可解释性
  • 数理逻辑具有很强的表达能力
• 覆盖：cover，符合某规则的样本称为被该规则覆盖
  • 例子：
  • 规则1：\(好瓜 \leftarrow （根蒂=蜷缩） \wedge（脐部=凹陷）\)
  • 规则2：\(\neg好瓜 \leftarrow （纹理=模糊）\)
  • 被规则1覆盖的是好瓜，但未被规则1覆盖的未必不是好瓜
  • 被规则2覆盖的是好瓜，但未被规则2覆盖的不是好瓜。因为此时的规则头带有\(\neg\)标签
• 冲突：
  • conflict
  • 规则集合中的每一条规则可看做一个模型
  • 当同一个示例被判别结果不同的多条规则覆盖时，发生冲突
  • 冲突消解：
    • conflict resolution
    • 投票法：判别规则数多的一类结果
    • 排序法：在规则集合上定义顺序，冲突时使用排序最前的规则。带序规则或者优先级规则
    • 元规则法：根据领域知识事先设定一些元规则，即关于规则的规则，比如”发生冲突时使用长度最短的规则“
• 默认规则：
  • default rule
  • 有的样本不能被所有规则所覆盖
  • 处理未被覆盖的样本，比如设置默认规则：未被规则1、2所覆盖的瓜不是好瓜
• 形式分类：
  • 命题规则：原子命题和逻辑连接词构成的简单陈述句。
  • 一阶规则：所有自然数加1都是自然数，这种就是一阶规则，可以写成表达式：\(\forall X(自然数(\sigma(X)) \leftarrow 自然数(X), sigma(X)=X+1)\)
    • 能表达复杂的关系，也称为关系型规则(relational rule)
  • 命题规则是一阶规则的一个特例，一阶规则的学习复杂得多

序貫覆盖

• 规则学习目标：产生一个能覆盖尽可能多的样本的规则集
• 序貫覆盖：
  • sequential covering
  • 最直接做法
  • 逐条归纳
  • 在训练集上每学到一条规则，就将该规则覆盖的训练样本去除，然后以剩下的训练样本组成训练集重复上述过程
  • 每次只处理一部分数据，也称为分治策略
• 关键：如何从训练集学出单条规则
  • 寻找最优的一组逻辑文字构成规则体
  • 搜索问题
• 最简单做法：
  • 从空规则开始
  • 将正样本类别作为规则头，逐个遍历训练集中的每个属性及取值，尝试将其作为逻辑文字增加到规则体中
  • 若能使当前规则仅覆盖正样本，则产生一条规则

  • 去除此规则所覆盖的正样本，尝试生成下一条规则

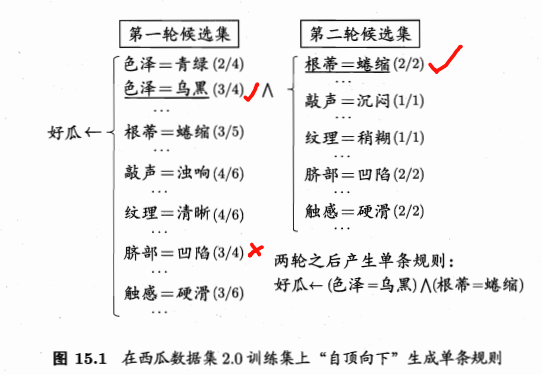
  • 例子：西瓜训练集2.0
  • 根据第一个样本加入规则：\(\neg好瓜 \leftarrow （色泽=亲绿）\)
  • 此规则覆盖样本1，6，10，17，其中2个正样本，2个负样本，不符合规则的条件
  • 尝试基于”色泽“的其他原子命题：”色泽=乌黑“，亦不能满足
  • 基于”色泽“不能产生一条规则，所以返回”色泽=青绿“，尝试增加一个基于其他属性的原子命题，比如”根蒂=蜷缩“，\(好瓜 \leftarrow （色泽=青绿） \wedge（根蒂=蜷缩）\)
  • 此规则覆盖了负样本17，不行
  • 更换基于”根蒂“的其他原子命题：\(好瓜 \leftarrow （色泽=青绿） \wedge（根蒂=稍蜷）\)
  • 此规则不覆盖任何负样本，符合规则的条件
  • 保留此规则，去掉其覆盖的正样本6，将剩下的样本作为训练集。重复进行规则生成。
  • 最后可得到一个序贯覆盖学习的结果：
  • 缺点：基于穷尽搜索，在属性和候选值较多事出现组合爆炸
• 现实策略：
  • 自顶向下：top-down，从比较一般的规则开始，逐渐添加新文字以缩小规则覆盖范围，直到满足预定条件为止。规则逐渐特化的过程，也称为生成-测试法。
  • 自底向上：bottom-up，从比较特殊的规则开始，逐渐删除文字以扩大规则覆盖范围，直到满足条件为止。规则逐渐泛化的过程，也称为数据驱动法。
  • 自顶向下：容易获得泛化性能较好的规则，对噪声的鲁棒性更强。命题规则学习通常使用。
  • 自底向上：更适合训练样本较少的情形。一阶规则学习这类假设空间很复杂的任务上使用。
• 自顶向下：
  • 空规则开始
  • 准确率评估规则好坏
  • 第一轮：两个相同准确率（3/4），选择次序靠前的
  • 第二轮：5个相同的准确率(100%)，选择覆盖样本最多、且属性次序最靠前的。

  • 对于这里：先准确率，相同时考虑覆盖样本数，再相同时考虑属性次序。具体可自行设计。

  • 每次仅考虑一个”最优“
  • 贪心：易限于局部最优
  • 做法：集束搜索（beam search），每轮保留最优的b个逻辑文字，在下一轮均用于创建候选集，再把候选集中最优的b个留待下一轮使用
• 序贯覆盖：
  • 简单有效
  • 基本框架，可扩展至其他规则学习
  • 多分类问题：当学习第c类的规则时，将所有 属于类别c的为正样本，其他均为负样本

剪枝优化

• 规则生成：贪心搜索过程，容易过拟合
• 缓解过拟合：
  • 剪枝
  • 预剪枝：在规则生长过程中

  • 后剪枝：发生在规则产生后

  • 性能指标：评估增加、删除逻辑文字前后的规则性能，判断是否需要剪枝
  • 借助统计性显著性检验：CN2算法
  • 使用似然率统计量（likelihood ratio statistics，LRS）：\(m_+,m_-\)：训练集正负样本，\(\hat m_+,\hat m_-\)：规则覆盖的正负样本
  • 衡量规则覆盖的样本分布与经验分布的差别：值越大，说明差别越大；值越小，说明规则的效果可能是偶然现象。
  • 一般设置LRS很大：比如0.99，才让算法停止生长
• 后剪枝：
  • 减错剪枝，reduced error pruning，REP
  • 将样本集划分为训练集和验证集
  • 从训练集学得规则集合
  • 对规则集合进行多轮剪枝：每一轮穷举可能的剪枝操作，然后用验证集对剪枝产生的所有候选规则集进行评估，保留最好的那个规则集进行下一轮剪枝

  • 重复，直到通过剪枝无法提高验证集的性能为止

  • 有效

  • 复杂度太高

  • IREP：incremental REP
  • 在生成每条规则前，先将当前样本集划分为训练集和验证集
  • 在训练集山生成一条规则r，立即在验证集上对其进行REP剪枝，得到规则r’
  • 将r’覆盖的样本去掉，在更新后的数据集上重复上述过程
  • IREP：对单条规则进行剪枝，更加高效
  • REP：针对规则集进行剪枝
• RIPPER：
  • 泛化性能超过很多决策树
  • 学习速度更快
  • 将剪枝和后处理优化相结合
  • 剪枝+后处理：
  • 对于R中的每条规则\(r_i\)，会产生两个变体：
  • \(r_i'\)：基于\(r_i\)覆盖的样本，用IREP*重新生成一条规则\(r_i'\)，称为替代规则(replacement rule)
  • \(r_i''\)：对\(r_i\)增加文字进行特化，然后使用IREP*剪枝生成一条规则\(r_i''\)，称为修订规则(revised rule)

  • 把\(r_i'\)和\(r_i''\)分别与R中除了\(r_i\)之外的规则放在一起，组成规则集R’和R‘’，与R进行比较，选择最优的保留下来。

  • 为什么更好？
  • 之前：按序生成规则，每条规则没有考虑对其后产生的规则，属于贪心算法，容易陷入局部最优
  • 现在：后处理优化过程中将R中的所有规则放在一起重新加以优化，是通过全局的考虑来缓解贪心算法的局部性，从而得到更好的效果。

一阶规则学习

• 命题逻辑：难以处理对象之间的关系
  • 挑西瓜：很难把西瓜的特征用具体的属性值描述出来
  • 现实：西瓜之间进行比较。命题逻辑难以胜任。
• 关系数据：根据属性的比较，可以把训练集转换为关系集
• 一阶规则：
  • 规则头、规则体：一阶逻辑表达式
  • 可表达递归概念：\(更好(X,Y) \leftarrow 更好(X,Z) \wedge 更好(Z,Y)\)
  • 容易引入领域知识
• FOIL：
  • first-order inductive learner
  • 著名的一阶规则学习算法
  • 遵循序罐覆盖框架且采用自顶向下的规则归纳策略
  • 使用“FOIL增益”来选择文字：\(F_{Gain}=\hat m_+ \times (log_2{\frac{\hat m_+}{\hat m_+ + \hat m_-}} - log_2{\frac{m_+}{m_+ + m_-}})\)
  • vs 决策树增益：仅考虑正样本的信息量，并使用新规则覆盖的正样本数作为权重

归纳逻辑程序设计

• 归纳逻辑程序设计
  • ILP：inductive logic programming
  • 一阶规则学习中引入函数和逻辑表达式嵌套
  • 具备强大的表达能力
  • 解决基于背景知识的逻辑程序归纳
• 函数和表达式嵌套的挑战：
  • 给定一元谓词P、一元函数f
  • 组成的文字有无穷多个
  • 候选原子公式有无穷多个
  • 若采用自顶向下的规则生成，在规则长度很大时无法列举而失败

最小一般泛化

• 归纳逻辑：
  • 自底向上
  • 一个正样本作为初始
  • 对规则进行逐步泛化
• 泛化：
  • 将规则中的常量替换为逻辑变量
  • 删除规则中的某个文字
• 最小一般泛化：
  • LGG：least general generalization

  • 把特殊的规则转变为更一般的规则

  • 给定一阶公式r1,r2
  • 先找出涉及相同谓词的文字
  • 对文字的每个位置的常量进行考察
  • 若常量在两个文字中相同则保持不变，记为：\(LGG(t,t)=t\)
  • 若不同则替换为用一个新变量，且变换应用于公式其他位置，记为：\(LGG(s,t)=V\)，V是新变量
  • 例子：
• LGG是能特化为r1和r2的所有一阶公式中最为特殊的一个:BU 不存在既能特化为r1和r2，也能泛化为他们的LGG的一阶公式r‘。

逆归结

• 演绎：从一般性规律出发来探讨具体事物。代表：数学定理证明
• 归纳：从个别事物出发概括出一般性规律。代表：机器学习
• 归结原理：
  • resolution principle
  • 一阶谓词演算中的演绎推理能用一条十分简洁的规则描述
  • 将复杂的逻辑规则与背景知识联系起来化繁为简
  • 逆归结：基于背景知识来发明新的概念和关系

参考

• 机器学习周志华第15章