Home > MachineLearning > Main text

强化学习

Tag: python, machine learning
2019-01-15

目录

任务与奖赏

如何种西瓜？

  • 选种
  • 定期浇水、施肥等【执行某个操作】
  • 一段时间才收获西瓜

  • 收获后才知道种出的瓜好不好【好瓜是辛勤种植的奖赏】

  • 执行操作后，不能立即获得最终奖赏

  • 难以判断当前操作对最终操作的影响

  • 强化学习：reinforcement learning
    • 需要多次种瓜，在种瓜过程中不断摸索，然后才能总结出好的种瓜策略

    • 这种过程的抽象

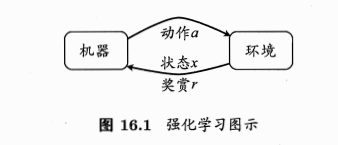
    • 通常用马尔科夫决策过程描述：MDP（markov decision process）20190817155741
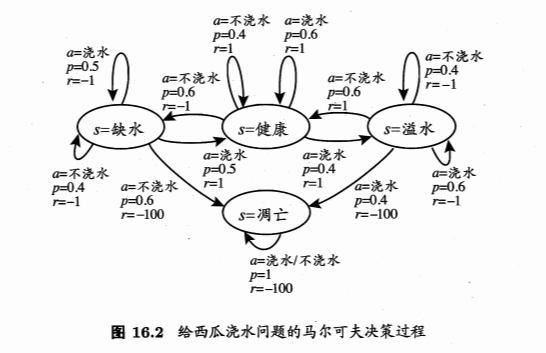
    • 机器处于环境E中，状态空间为X，每个状态\(x\in X\)是机器感知到的环境的描述（如瓜苗的长势好不好的描述）
    • 机器可采取的动作空间A：比如浇水、施肥
    • 状态转移：某个动作a作用在当前状态x上，潜在的转移函数P使得环境从当前状态按照某种概率转移到另一个状态。如x=缺水，a=浇水，则瓜苗的长势发生变化，一定概率恢复健康，也一定概率无法恢复。

    • 奖赏：在转移到另一个状态时，根据潜在的奖赏函数R反馈给机器一个奖赏，如健康+1，凋零-10

    • 模型对应四元组：\(E=<X,A,P,R>\)
    • \(P: X\times A\times X \longmapsto R\)：状态转移概率
    • \(R: X\times A\times X \longmapsto R\)：奖赏
  • 西瓜浇水的马尔科夫决策过程：
    • 4个状态：健康、缺水、溢水、凋亡
    • 2个动作：浇水、不浇水
    • 状态保持健康+1；缺水/溢水-1；凋亡-100且无法恢复 20190817160746
  • 机器 vs 环境：
    • 环境中的状态转移、奖赏返回不受机器控制
    • 机器可通过选择动作影响环境
  • 策略：
    • 机器的核心：学习策略
    • 通过在环境中不断尝试而学得一个策略(policy) \(\pi\)

    • 根据这个策略，在状态x下就能得知要执行的动作\(a=\pi(x)\)

    • 策略表示方法：
    • 【1】函数表示：\(\pi: X \longmapsto A\)，确定性策略表示

    • 【2】概率表示：\(\pi: X \times A \longmapsto R\)，随机性策略表示，当前状态x下选择动作a的概率

    • 策略好坏？
    • 取决于长期执行这一策略后得到的累计奖赏
    • 强化学习目的：找到能使长期累计奖赏最大化的策略
    • 计算方式：
      • T步累计奖赏
      • \(\gamma\)折扣累计奖赏
  • 强化学习 vs 监督学习：
    • 状态 =》 样本
    • 动作 =》 标记
    • 策略 =》 分类器或者回归器

    • 模型形式无差异

    • 强化学习没有有标记样本，没有直接可以告诉机器在什么状态下采取什么动作。
    • 只有等最终结果揭晓，才能通过”反思“之前的动作是否正确进行学习
    • 某种意义：延迟标记信息的监督学习问题

K-摇臂赌博机

探索-利用窘境

最大化单步奖赏：

  • 最终奖赏的简单情况
  • 仅考虑一步操作

  • 通过尝试发现各个动作产生的结果

  • 需考虑2个方面：
    • 每个动作的奖赏
    • 执行奖赏最大的动作
    • 注意：如果每个动作的奖赏是确定值，直接尝试，选最大的即可。通常一个动作的奖赏值来于一个概率分布，仅一次尝试不能确切获得平均奖赏值。

单步强化学习：

  • 理论模型：K-摇臂赌博机
  • 有K个摇臂，在投入一个硬币后可选择按下一个摇臂，每个摇臂以一定概率吐出硬币，但是这个概率赌徒是不知道的

  • 赌徒目标：通过一定的策略最大化自己的奖赏

  • 仅探索法：
    • exploration-only
    • 若仅为了获知每个摇臂的期望奖赏
    • 所有的尝试机会平均分配给每个摇臂，各自的平均吐币概率作为奖赏概率的近似估计
    • 很好的估计每个摇臂的奖赏
    • 失去很多选择最优摇臂的机会
  • 仅利用法：
    • exploitation-only
    • 若仅为了执行奖赏最大的动作
    • 按下目前最优的摇臂（即目前为止平均奖赏最大的），若多个最优，随机选取一个
    • 不能很好的估计每个摇臂的奖赏
  • 两者都难以使最终的累计奖赏最大化
  • 探索-利用窘境：
    • 尝试次数有限
    • 一方加强则另一方削弱
    • 需在探索和利用之间达成较好的折中

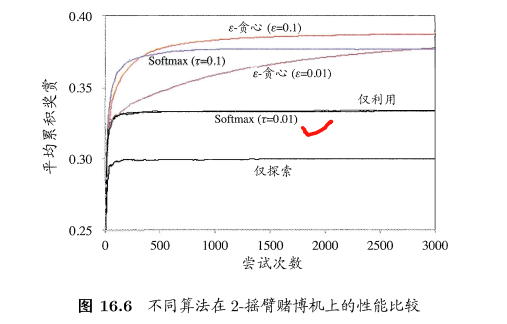
\(\epsilon\)-贪心

  • 基于概率对探索和利用进行折中
  • 每次尝试，以\(\epsilon\)概率进行探索，以均匀概率随机选取一个摇臂
  • 以\(1-\epsilon\)概率进行利用，选择当前平均奖赏最高的摇臂
  • 摇臂k的平均奖赏：\(Q(k)=\frac{1}{n}\sum_1^nV_i\)，k此尝试的奖赏的均值
  • 问题：对于每个臂的计算，都需要n个记录值，不够高效
  • 做法：对均值进行增量式计算，每尝试一次就立即更新\(Q(k)\)
    • n-1 =》 n：\(Q_nk=\frac{1}{n}{(n-1)\times Q_{n-1}(k)+v_n}=Q_{n-1}(k)+\frac{1}{n}(v_n - Q_{n-1}(k))\)
    • 只需记录两个值：已尝试次数n-1; 最近平均奖赏 \(Q_{n-1}(k))\) 20190817164255
  • 若概率分布较宽（不确定性大），需更多的探索，需较大的\(\epsilon\)
  • 若概率分布较集中（不确定性小），需少的探索，需较小的\(\epsilon\)
  • 通常：取较小的常熟，如0.1，0.01
  • 如果尝试次数很大，可逐渐减小\(\epsilon\)值

Softmax

  • 基于当前已知的摇臂平均奖赏对探索和利用进行折中
  • 若各摇臂平均奖赏相当，则选取概率也相当
  • 若某些奖赏高于其他，则被选取概率也更高
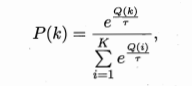
  • 摇臂概率分配基于玻尔兹曼分布：20190817164922
  • \(Q(i)\)：当前摇臂的平均奖赏
  • \(\tau>0\)：温度，越小则平均奖赏高的摇臂被选取的概率越高
  • \(\tau\)趋于0：趋于仅利用
  • \(\tau\)趋于无穷大：趋于仅探索

  • 算法描述：20190817165141

  • Softmax vs \(\epsilon\)-贪心
    • 好还取决于具体应用
    • 例子：2-摇臂机，臂1返回奖赏1概率是0.4，返回0概率是0.6；臂2返回奖赏1概率是0.2，返回0概率是0.8
    • 平均累计奖赏如下：20190817165406
    • 不同的参数条件下不一样

有模型学习

  • 上面的是单步强化学习
  • 实际：多步强化学习
  • 模型已知：假设任务对应的马尔科夫决策过程四元组已知（即机器对环境进行了建模，能在机器内部模拟出与环境相同或近似的状况）
  • 状态x执行动作a到状态x‘的转移概率、对应的奖赏已知

策略评估

  • 模型已知，能评估任意策略的期望累计奖赏
  • 状态值函数：state value function，\(V^\pi(x)\)，从状态x出发，使用策略\(pi\)带来的累计奖赏【指定状态】
  • 状态-动作值函数：state-action value function，\(Q^\pi(x,a)\)：从状态x出发，执行动作a后，再使用策略\(pi\)带来的累计奖赏【指定状态-动作】
  • 马尔科夫性质计算值函数：
    • 马尔科夫性质
    • 递归（动态规划）20190817171147

策略改进

  • 策略进行累计奖赏评估后，发现不是最优策略，希望改进
  • 理想的策略应该是能够最大化累计奖赏的：\(\pi^* = arg max \sum_{x \in X}V^{\pi}(x)\)
  • 一个强化学习可能有多个最优策略，最优值函数
  • 20190817201658

策略迭代与值迭代

  • 前面：如何评估一个策略的值函数+评估策略后改进
  • 策略迭代：policy iteration，结合以找到最优解
    • 从一个初始策略出发
    • 先进行策略评估，然后改进策略
    • 评估改进的策略，再进一步改进策略
    • 。。。
    • 不断迭代评估和改进
    • 直到策略收敛、不再改变
  • 基于T步累计奖赏的策略迭代：20190817202040
  • 基于T步累计奖赏的值迭代：
    • value iteration
    • 策略迭代需每次改进策略后重新进行评估
    • 比较耗时
    • 策略改进与值函数的改进是一致的
    • 可将策略改进视为值函数的改善 20190817202317
  • 模型已知：
    • 强化学习 =》 基于动态规划的寻优问题
    • 与监督学习不太，不涉及泛化能力，而是为每一个状态找到最好的动作

免模型学习

  • 现实：环境的转移概率、奖赏函数难以得知
  • 免模型学习：
    • model-free learning
    • 学习算法不依赖于环境建模
    • 比有模型学习困难得到

蒙特卡罗强化学习

  • 策略迭代问题：如何品谷策略？模型未知不能做全概率展开
  • 通过在环境中执行动作，以观察专一的状态和得到的奖赏
    • 策略评估替代方案：多次采样，求平均
    • 蒙特卡罗强化学习
  • 策略迭代算法：估计状态值函数V
    • 由V退出状态-动作值函数Q
    • 模型已知时，容易
    • 未知时困难
    • 估计对象从V转变为Q：估计状态-动作值函数
  • 评估过程：
    • 从起始状态出发，使用某种策略进行采样
    • 执行该策略T步获得轨迹：\(<x_0,a_0,r_q,...,x_{T-1},a_{T-1},r_{T-1}>\)
    • 对轨迹中出现的每一对状态-动作，记录奖赏之和，作为其一次采样
    • 多次采样获得多个轨迹

    • 每个状态-动作的累计奖赏采样值求和取平均，得到状态-动作值函数的估计

    • 策略是确定性的，对策略进行采样，可能得到的是多个相同的轨迹
    • 而我们需要不同的采样轨迹
    • 可使用\(\epsilon\)贪心法
    • 以\(\epsilon\)的概率从所有动作中随机选取一个，以\(1-\epsilon\)的概率选取当前最优动作
    • 这样多次采样会产生不同的采样轨迹
  • 策略改进：
    • 可以以同样的策略进行改进
    • 因为引入的贪心策略是均匀分配给所有动作的
  • 同策略蒙特卡罗强化学习：
    • on-policy
    • 被评估和改进的是同一个策略 20190817204134
  • 异策略蒙特卡罗强化学习：
    • off-policy 20190817204252

时序差分学习

  • 蒙特卡罗：
    • 考虑采样轨迹，克服模型未知给策略评估造成的困难
    • 完成采样轨迹后进行评估，效率低下
    • 没有充分利用强化学习任务的MDP结构
  • 时序差分：
    • temporal difference
    • 结合动态规划和蒙特卡罗的思想
    • 更高效的免模型学习
  • 蒙特卡罗：求平均是批处理式的
  • 增量式进行：
    • 从t时刻到t+1时刻的增量 20190817204927
  • 每执行一步策略就更新一次值函数估计
  • Sarsa算法：
    • 同策略算法
    • 评估\(\epsilon\)-贪心策略
    • 执行\(\epsilon\)-贪心策略
    • 更新需知道：State前一步状态, Action前一步动作, Reward奖赏值, State当前状态, Action将执行动作【这也是使用了马尔科夫的性质的体现】
  • Q-学习算法：
    • 异策略算法
    • 评估\(\epsilon\)-贪心策略
    • 执行原始策略 20190817205416

值函数近似

  • 强化学习：
    • 有限空间状态，每个状态可用一个编号指代
    • 值函数：关于有限状态的表格值函数，数组表示，i对应的函数值就是数组i的值
  • 状态空间是连续的？无穷多个状态？
    • 状态空间离散化：转换为有限空间后求解

    • 转换：是难题

    • 直接对连续状态空间进行学习
    • 简化情形：值函数为状态的线性函数：\(V_{\theta}(x)=\theta^Tx\)
    • x：状态向量，\(\theta\)：参数向量
    • 此时的值函数难以像有限状态那样精确记录，这种求解是值函数近似（value function approximation）
  • 线性值函数近似：20190817210623

模仿学习

  • 模仿学习：
    • imitation learning
    • 现实任务中，往往能得到人类专家的决策过程范例，从这样的范例中学习，就是模仿学习

直接模仿学习

  • 多步决策搜索空间巨大

  • 缓解：直接模仿人类专家的“状态-动作对”

  • 人类专家轨迹数据集：\(\{\tau_1,\tau_2,...,\tau_m\}\)
  • 每条轨迹包含状态+动作：\(\tau_i=<s_1^i,a_1^i,...,s_{n_i+1}^i>\), \(n_i\):第i条轨迹的转移次数
  • 数据 =》在什么状态下选择什么动作，可利用监督学习
  • 抽取“状态-动作”对：
    • 新数据集：\(D=\{(s_1,a_1),(s2,a_2),...\}\)
    • 特征：状态
    • 标记：动作
    • 使用分类或回归算法学得策略模型

逆强化学习

  • 现实任务：设计奖赏函数很困难
  • 逆强化学习：
    • 从人类专家提供的范例数据中反推奖赏函数有助于解决该问题
    • inverse reinforcement learning
  • 基本思想：
    • 使机器做出与范例一致的行为，等价于在某个奖赏函数的环境下寻求最优策略，该策略所产生的轨迹与范例数据一致。
    • 寻找某种奖赏函数使得范例数据最优，然后使用这个奖赏函数来训练强化学习策略
  • 算法：
    • 从随机策略开始
    • 迭代求解更好的奖赏函数
    • 基于奖赏函数获得更好的策略
    • 直到最终获得最符合范例轨迹数据集的奖赏函数和策略 inverse_reinforcement_learning.jpeg

参考

  • 机器学习周志华第16章

If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/reinforcement-learning.html
Previous: 【1-1】深度学习引言

    Category

    Latest articles

    Links