目录
二分类
- 神经网络:对于m个样本,通常不用for循环去遍历整个训练集
- 神经网络的训练过程:
- 前向传播:forward propagation
- 反向传播:backward propagation
-
例子:逻辑回归
- 二分类:
- 目标:识别图片是猫或者不是
- 提取特征向量:3通道的特征向量,每一个是64x64的,最后是64x64x3
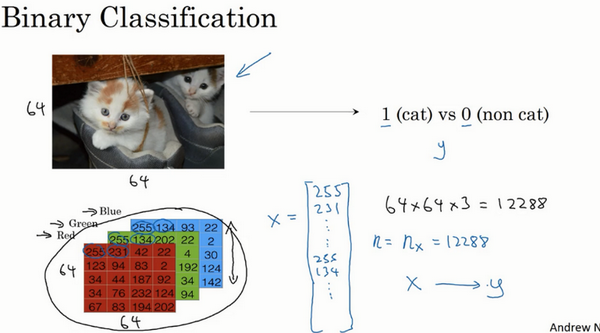
- 符号表示:
- 训练样本的矩阵表示X:每一个样本是一列,矩阵维度:特征数x样本数
- 输出标签y:矩阵维度:1x样本数

逻辑回归
- 二分类:
- 输入特征向量,判断是不是猫
- 算法:输出预测值\(\hat y\)对实际值\(y\)的估计
- 正式的定义:让预测值\(\hat y\)表示实际值\(y\)等于1的可能性
- 例子:
- 图片识别是否是猫
- 尝试:\(\hat y=w^Tx+b\),线性函数,对二分类不是好的算法,因为是想“让预测值\(\hat y\)表示实际值\(y\)等于1的可能性”,所以\(\hat y\)应该在【0,1】之间。
- sigmoid函数:
- 当z很大时,整体值接近于1(1/(1+0))
- 当z很小时,整体值接近于0(1/(1+很大的数))
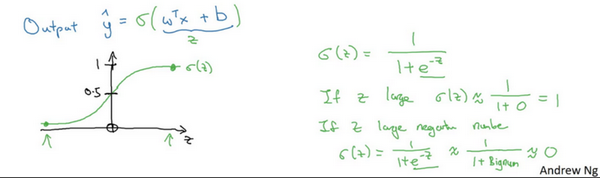
- 让机器学习参数\(w\)及\(b\),使得\(\hat y\)称为对\(y=1\)这一情况的概率的一个很好的估计。
逻辑回归的代价函数
- 损失函数L:
- 衡量预测输出值与实际值有多接近
- 一般使用平方差或者平方差的一半
- 逻辑回归损失函数loss function:
- 逻辑回归如果也使用平方差:
- 优化目标不是凸优化的
- 只能找到多个局部最优解
- 梯度下降法很可能找不到全局最优
- 逻辑回归使用对数损失:\(L(\hat y, y)=-ylog(\hat y)-(1-y)log(1-\hat y)\)
- 单个样本的损失
- 为啥是这个损失函数?【直观理解】
- 当y=1时,损失函数\(L=-log(\hat y)\),L小,则\(\hat y\)尽可能大,其取值本身在[0,1]之间,所以会接近于1(也接近于此时的y)
- 当y=0时,损失函数\(L=-log(1-\hat y)\),L小,则\(1-\hat y\)尽可能大,\(\hat y\)尽可能小,其取值本身在[0,1]之间,所以会接近于0(也接近于此时的y)
- 逻辑回归如果也使用平方差:
- 代价函数cost function
- 参数的总代价
- 对m个样本的损失函数求和然后除以m
- 为什么是这个损失函数?
- 多样本的代价函数
梯度下降法
- 逻辑回归的代价函数是凸函数(convex function),像一个大碗一样,具有一个全局最优。如果是非凸的,则存在多个局部最小值。

- 梯度下降:
- 初始化w和b参数。逻辑回归,无论在哪里初始化,应该达到统一点或大致相同的点。
- 朝最陡的下坡方向走一步,不断迭代
- 直到走到全局最优解或者接近全局最优解的地方
- 迭代:
- 公式:\(w := w - \alpha \frac{dJ(w)}{dw} 或者 w := w - \alpha \frac{\partial J(w,b)}{\partial w}\)
- 学习速率:\(\alpha\),learning rate,控制步长,向下走一步的长度
- 函数J(w)对w求导:\(\frac{dJ(w)}{dw}\),就是斜率(slope)
- 偏导:\(\partial\)表示,读作round,\(\frac{\partial J(w,b)}{\partial w}\)就是J(w,b)对w求偏导
-
在逻辑回归还有参数b,同样的进行迭代更新
- 一个参数:求导数(derivative),用小写字母d表示
- 两个参数:求偏导数(partial derivative),用\(\partial\)表示
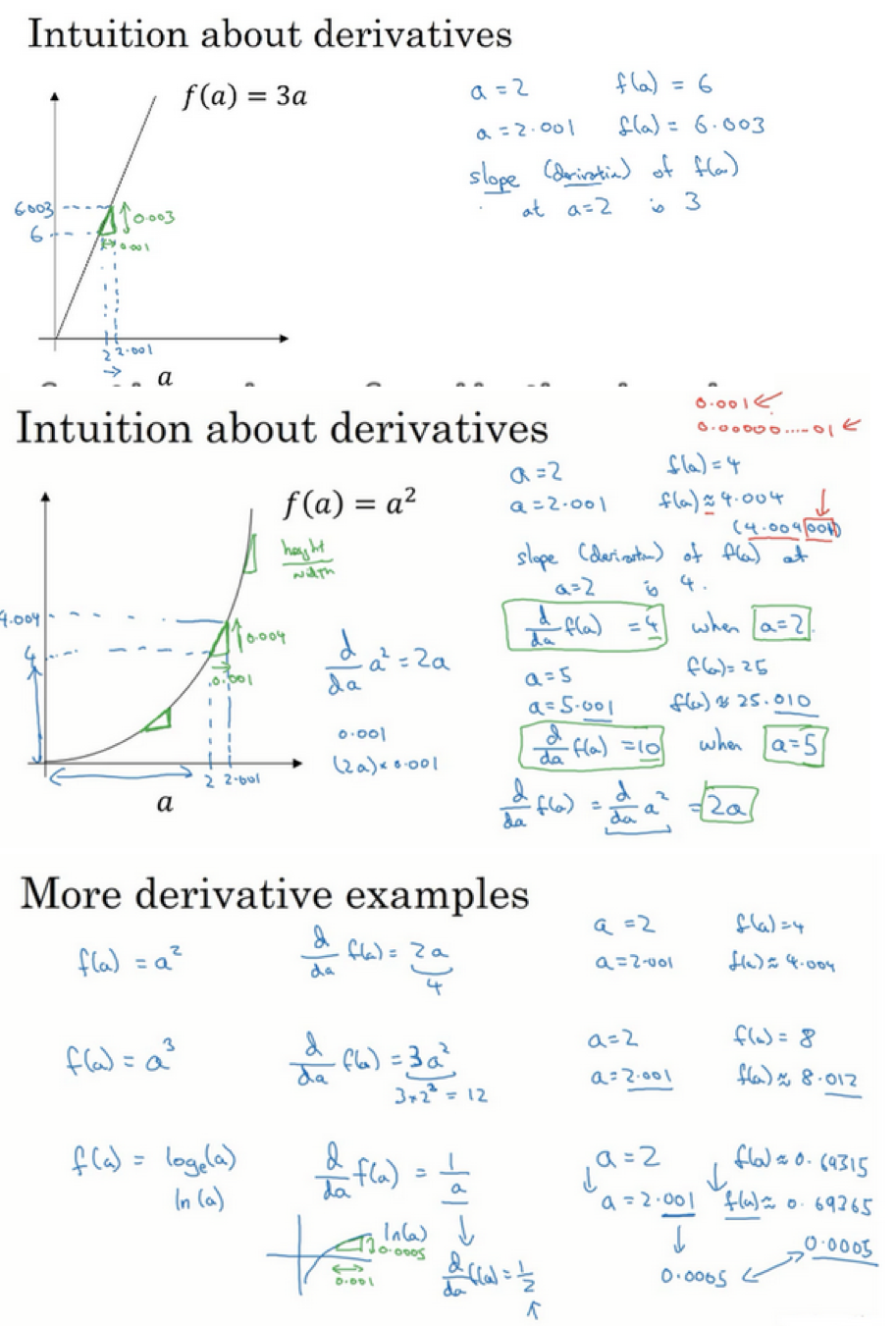
导数及例子
计算图
- 神经网络:按照前向或反向传播过程组织的
- 例子:计算函数J的值

- 计算J的值:从左向右的过程,蓝色箭头
- 计算导数:从右向左的过程,红色箭头
使用计算图求导数
- 在一个计算图中,计算导数
- 导数:最后输出的变量,对于某个你关心的变量的导数
- 直观做法:某个变量改变(增加)一点点(这里都是0.001),那么最后输出的变量改变(增加)了多少倍?这个倍数就是导数
- 需要使用到链式法则,改变一个变量,最先受到影响的是其最相近的变量,然后向后传播,直到影响最终的输出变量。
- 所以在计算导数的时候,是反向的,看离输出变量最近的变量的导数,再一次往回推。
- 这里是举得例子,核心:【1】小增量,【2】反向一次计算
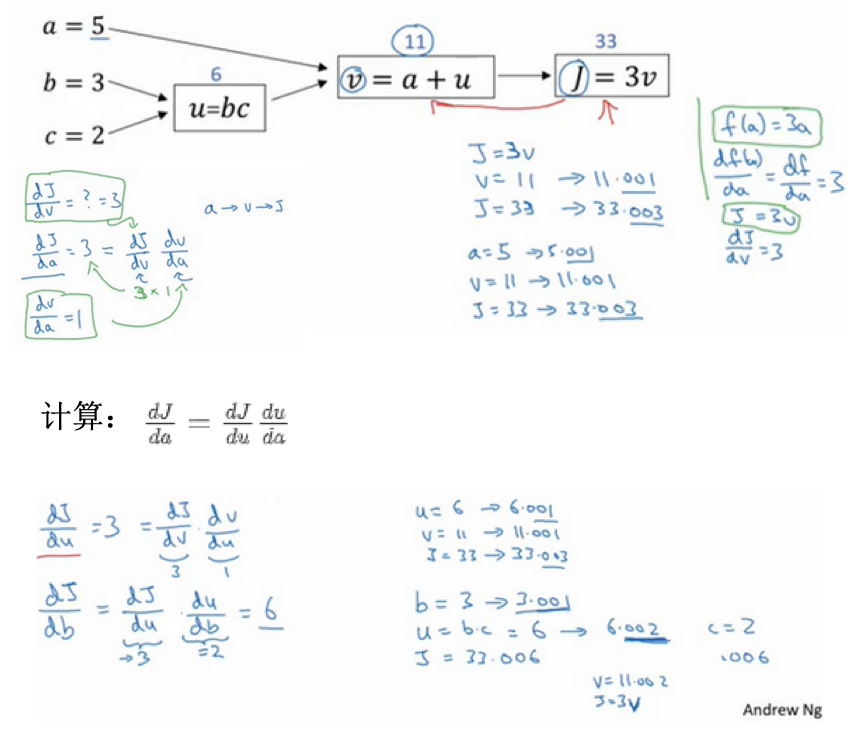
- 表示:\(dv,da,db\)等形式,分别表示最后的输出对于某个变量的导数,在编程时注意命名
逻辑回归中的梯度计算
- 单个样本
- 数据特征值:x1,x2
- 参数变量:w1,w2,b
- 构建计算图:特征值+参数变量值 =》计算Z值 =》计算预测值(逻辑回归变换)=》计算损失函数

- 单个样本各参数的导数
- 损失函数值对于每个参数的导数:单个样本就是计算单个样本的损失函数
- 链式法则,反向计算

- 多样本(m)的梯度下降
计算代码实现:
J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db
缺点:
- for循环
- 循环1:所有样本
- 循环2:所有特征,这里只假设有2个特征,所以只有w1和w2
- 需要向量化计算
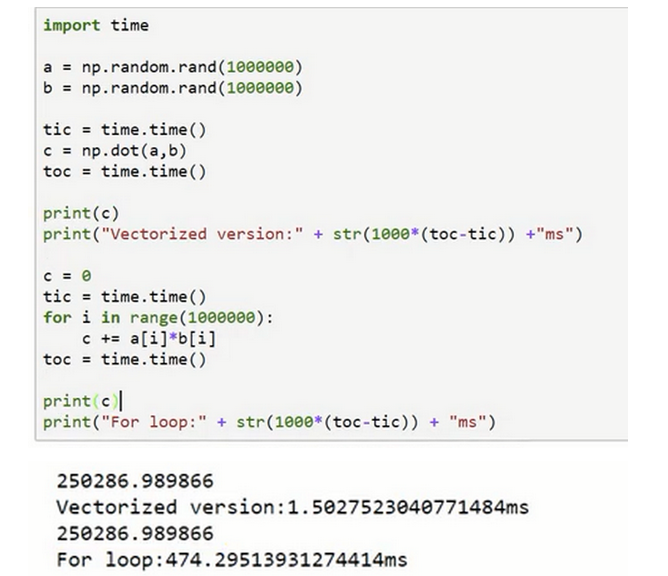
向量化
- 取代代码中的for循环,比如计算两个数组的对应元素乘积的和(W*X),可以使用for循环,但是向量化更简单(每个数组可看成一个向量)

-
尽量使用numpy内置的向量操作 * 比如向量乘积(dot) * 还有很多其他的:求指数,绝对值,倒数等

- 逻辑回归导数求解引入向量化
逻辑回归向量化
- 向量化前向传播:
- 传统:遍历每个样本,分别根据公式\(z^(i)=wTx^(i)+b\)计算z,再计算激活函数值a
- 向量化:

- 在numpy中:\(Z=np.dot(w.T, X)+b\),这里直接+b,实际使用了python重点额广播特性(broadcasting,自动填充)。计算了Z之后,直接调用sigmoid函数,可直接计算激活函数值。
- 向量化后向传播:
- 同时计算m个样本的梯度
- 之前:\(dz^{(1)}=a^{(1)}-y^{(1)}, dz^{(2)}=a^{(2)}-y^{(2)}, ...\)
- 构建:\(dZ=A-Y=[a^{(1)}-y^{(1)} a^{(2)}-y^{(2)} ...]\),这里的每个元素其实就是上面的导数
- 合在一起:
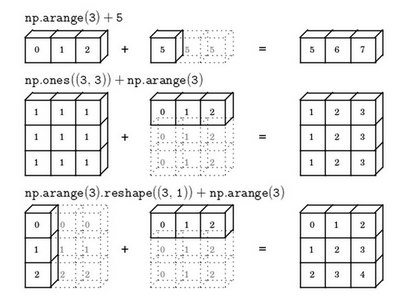
numpy广播机制
numpy向量:清除一维数组
- 广播功能:灵活,但是也可能出现bug
- 避免使用一位数组,使用向量
- 在随机生成函数中,只指定数目时,得到的是一维数组a,其shape函数返回值是
(n,) - 此时不是向量,所以其有些操作看起来是奇怪的,比如a和a的转置的乘积,得到的只是一个数值,而不是向量
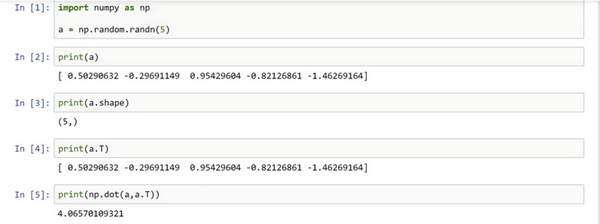
- 在随机生成函数中,只指定数目时,得到的是一维数组a,其shape函数返回值是
- 显示的指定向量维度:
- 使用assert判断维度:
assert(a.shape == (5,1)),可以避免其维度是(5,)的情况 - 使用reshape更改为指定的维度
参考
If you link this blog, please refer to this page, thanks!
Post link:https://tsinghua-gongjing.github.io/posts/neural-networks-and-deep-learing-1-programming.html
Previous:
强化学习
Next:
【1-3】浅层神经网络
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me