12: Support Vector Machines
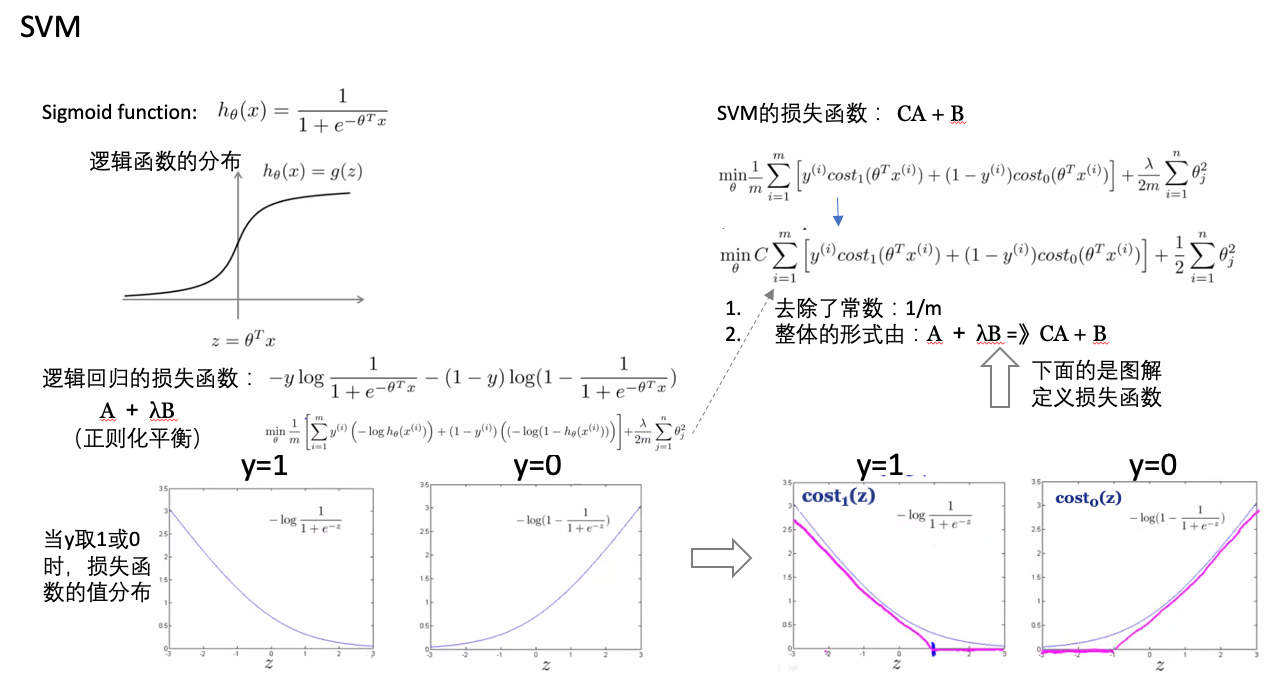
- 损失函数:
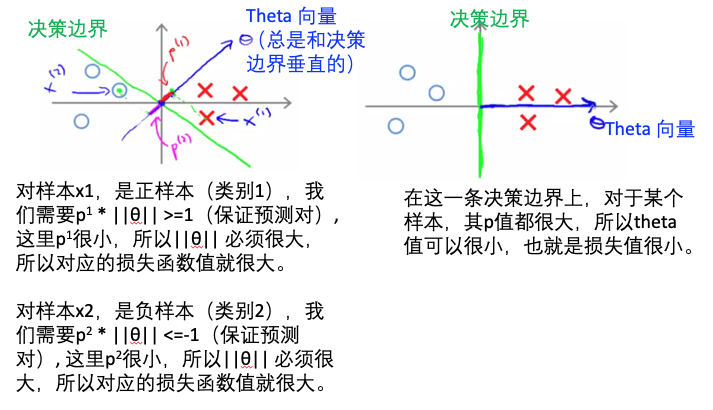
- SVM vs logistic regression决策边界的比较:
- 与逻辑回归相比,SVM是更稳健的,因为其选择的是最大距离(large margin),比如下图中逻辑回归选择了黄绿的边界,能够将现有数据分隔开,但是泛化能力差;黑色的是SVM选择的边界(最大化距离)。
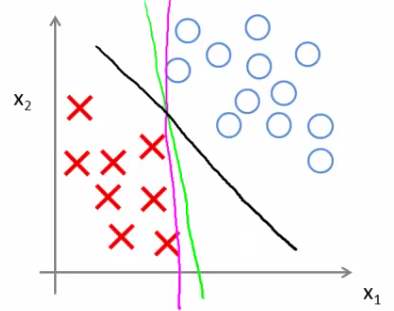
- 与逻辑回归相比,SVM是更稳健的,因为其选择的是最大距离(large margin),比如下图中逻辑回归选择了黄绿的边界,能够将现有数据分隔开,但是泛化能力差;黑色的是SVM选择的边界(最大化距离)。
- 核(kenel):
- 多项式拟合hθ(x) = θ0+ θ1 x f1+ θ2 x f2 + θ3 x f3:
- f1=x1, f2=x1x2, f3=… ,基于特征的组合进行多项式拟合(指定的组合特征向量再乘以权重矩阵)。
- h(x)=1,x<=0
- h(x)=0, x>0
- 多项式拟合计算消耗太大
- 对于空间中,选取某些点作为landmark(这些点是怎么选取的?随机的?),然后对于某个数据点(样本),计算数据点到landmark点之间的距离(相似性),比如用高斯核,计算的这个距离就是欧式距离。
- 相似性函数(similarity function):称为核
- 高斯核:
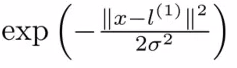
- 如果x距离landmark点很近,那么f1=e(-0)=1; 如果x距离lanmark点很远,那么f1=e(-large number)=0.
- 所以核函数就是定义某个点x距离landmark点的远近的,很近的时候值为1,很远的时候值为0。比如下面的例子是选择landmark点为[5,3],其他x1,x2值时距离此点的远近。
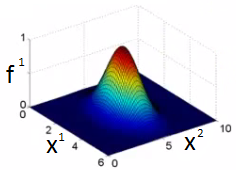
- 多项式拟合hθ(x) = θ0+ θ1 x f1+ θ2 x f2 + θ3 x f3:
- 基于核函数的非线性模型:
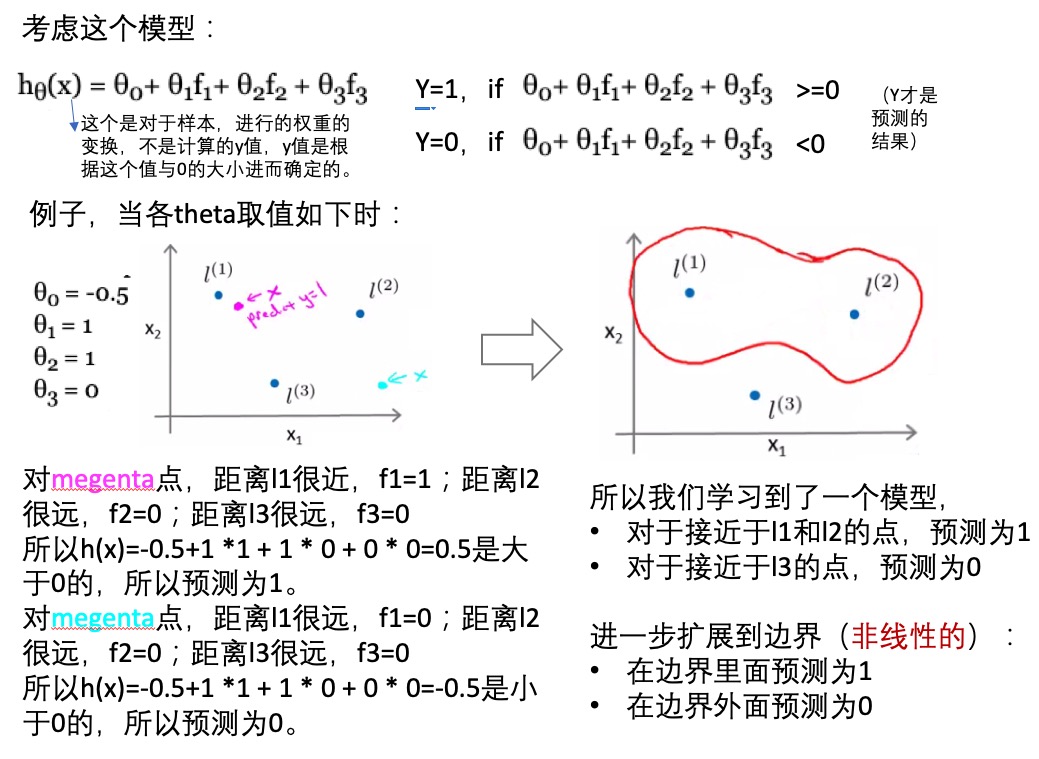
- 如何选取landmark(训练集全都放置一个):
- 对于训练集的每个样本,在其相同的位置放一个landmark,所以总共会有m个landmark
- 对于每个训练样本,计算特征向量:f0,f1,。。。,fm,其中恒有f0=1。有一个fi就是这个样本自己(因为上一步是每个样本都放置了一个landmark),此时fi=1。
- m个feature + f0 =》得到一个特征向量举证:[m+1, 1]维度的
- SVM训练:
- 现在有了特征向量,还有权重矩阵,如果他们的内积是>=0的,则预测的y=1,否则预测为y=0。所以现在需要训练得到权重矩阵!!!
- 有多少个样本m,就有多少个特征
- 使用之前提到的损失函数,训练的到最优的参数(权重矩阵)。在这里是对特征向量f进行优化,而不是原来的x。【xi =》fi,原来的i个特征值变成现在的与各个landmark点的距离远近】
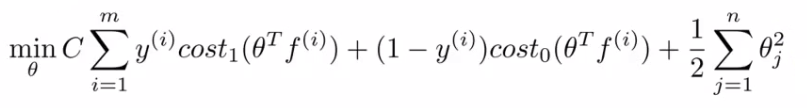
- SVM参数C(CA+B):
- 与正则化里面的1/lambda功能类似,平衡bias和variance
- 小的C:low bias high variance -》过拟合
- 大的C:high bias low variance -》欠拟合
- SVM参数σ2:
- 是在计算特征值f时用到的
- 小的σ2:特征值差异很大,low bias high variance
- 大的σ2:特征值差异较平滑,high bias low variance
- 高斯核:
- 需要定义方差σ2
- 什么时候使用高斯核:特征数n少或者样本数m大
- 在使用之前,必须进行特征缩放。【不然具有大值的特征会主导计算的特征值】
- 线性核:
- 当样本数m小,特征数n很大时:少样本、多特征
- 没有足够的数据
- SVM的多类别:
- 很多工具都支持
- 或者使用one-vs-all的方式
- 逻辑回归 vs SVM:
- 特征数目(n)相对于训练样本(m)很大时,使用逻辑回归或者SVM的线性核。比如文本分类问题:特征10000,训练集1000.
- 特征数目少(1-1000),样本数中等(10-10000),使用高斯核。
- 特征数目少(1-1000),样本数目很多(50000+):1)SVM+高斯核 =》会很慢;2)可以逻辑回归或者SVM线性核;3)手动的增加或者组合特征,增加特征数目。
- 逻辑回归和SVM线性核很相似:做的事情类似,效果相当
- SVM+多种不同的内核,可以构建非线性模型。很多时候神经网络也可以,但是SVM训练会快很多
- SVM是全局最小值,是凸优化的问题
- 通常难以选择最优算法:1)获取更多的数据;2)设计新的特征;3)算法debug
If you link this blog, please refer to this page, thanks!
Post link:https://tsinghua-gongjing.github.io/posts/CS229-12-SVM.html
Previous:
半监督学习
Next:
[CS229] 13: Clustering
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me