EM算法

Home > MachineLearning > Main text

Tag: python, machine learning

2018-07-25

最大似然

最大似然的想法经常被用到

具体到这个例子中，有如下过程：

假设\(\theta\)为黑球的占比，所以\(\theta_甲=0.01\)，\(\theta_乙=0.99\)
只取一次，只有1个样本，随机独立，所以每个样本服从\(p=\theta\)的伯努利分布
计算似然值（在不同\(\theta\)取值下，出现某个数据集的可能性）：
甲箱：\(ln P_X(x_1,...,x_n;\theta_甲)=\sum_{i=1}^nln(x_i;\theta_甲)=ln(0.01)\)
乙箱：\(ln P_X(x_1,...,x_n;\theta_甲)=\sum_{i=1}^nln(x_i;\theta_甲)=ln(0.99)\)
所以最可能的是乙箱

调查学校男女生身高

抽样男生100，女生100，量取身高，左手边是男生，右手边是女生（注意：男女生分开）
假设男生女生身高服从高斯分布，但是分布的均值和方差未知
需要估计模型参数：即均值和方差
从分布是\(p(x\|θ)\)的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率: \(L(\theta)=L(x_1,...,x_n;\Theta)=\prod p(x_i;\theta), \theta\subset\Theta\)
只有\(\theta\)是未知的，所以是\(\theta\)的函数
要使得\(L(\theta)\)取到最大值，值需要对\(\theta\)求导，求得导数=0时的\(\theta\)值即可。
函数：反应了在不同的参数\(\theta\)取值下，取的当前这个样本集的可能性，因此称为参数\(\theta\)相对于样本集\(X\)的似然函数。

最大似然的思想

内容：已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。
思想：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

求最大似然函数估计值的一般步骤

（1）写出似然函数；
（2）对似然函数取对数，并整理；
（3）求导数，令导数为0，得到似然方程；
（4）解似然方程，得到的参数即为所求；

为什么需要EM算法？

最大似然估计的拓展
模型的数据不完备：比如某些属性值是缺失的

EM算法原理：期望最大化算法（Expectation-Maximization）

原理

若参数\(\Theta\)已知，则可根据训练数据集推断出最优隐变量\(Z\)的值（E步）；反之，若最优隐变量\(Z\)的值已知，可方便的对参数\(\Theta\)做极大似然估计（M步）。

对模型参数\(\Theta\)做极大似然估计：

隐变量（latent variable）：未观测的变量\(Z\)
已观测变量集：\(X\)
模型参数：\(\Theta\)
最大化对数似然：\(LL(\Theta\|X,Z)=lnP(X,Z\|\Theta)\)
问题：\(Z\)是隐变量，无法直接进行求解

先计算隐变量的期望，再估计模型参数：

解决：通过对\(Z\)计算期望，来最大化已观测数据的对数边际似然（marginal likelihood）
对数边际似然：\(LL(\Theta\|X)=lnP(X\|\Theta)=ln\sum_{Z}P(X,Z\|\Theta)\)

EM步骤两步

基于\(\Theta^t\)推断隐变量\(Z\)的期望，记为\(Z^t\)
基于已观测变量\(X\)和\(Z^t\)对参数\(\Theta\)做极大似然估计，记为\(\Theta^(t+1)\)
交替直到收敛

EM图解

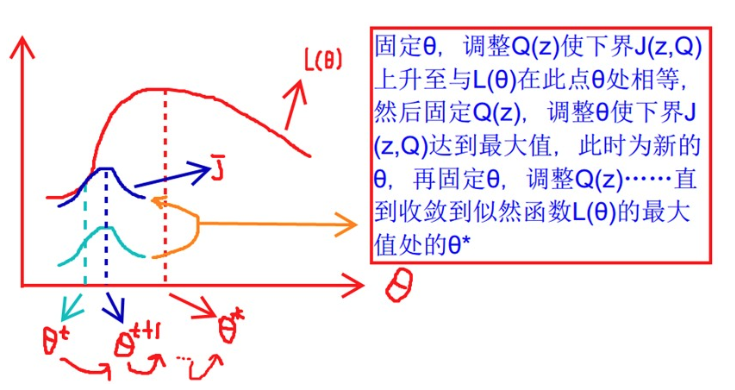
固定\(\theta\)，调整\(Q(z)\)使得下界\(J(z,Q)\)上升至于\(L(\theta)\)在此点\(\theta\)相等
然后固定\(Q(z)\)，调整\(\theta\)使得下界\(J(z,Q)\)达到最大值（\(\theta^t\)到\(\theta^(t+1)\)）
再固定\(\theta\)，调整\(Q(z)\)。。。
直到收敛到似然函数\(L(\theta)\)的最大值处\(\theta^*\)

EM算法特点

估计隐变量参数
是迭代算法

EM算法例子

调查学校男女生身高：引入隐变量

抽样男生100，女生100，量取身高，但是男女生是在一起的。
假设男生女生身高分别服从高斯分布，但是对应分布的均值和方差未知
问题：随便指定一个身高，不知道是来自男生还是女生？
描述：抽取得到的每个样本都不知道是从哪个分布抽取的
所以这里既有有了隐变量：抽取得到的每个样本都不知道是从哪个分布抽取的
需要估计模型参数：即各自的均值和方差

抛硬币的例子

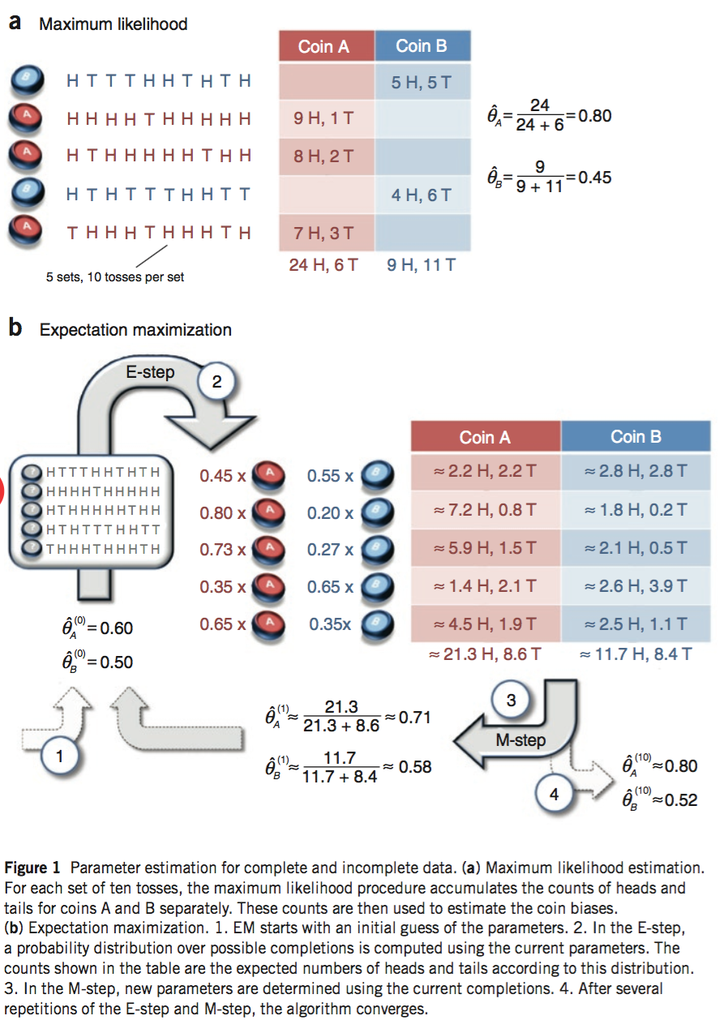
现在有两个硬币A和B，要估计的参数是它们各自翻正面（head）的概率。观察的过程是先随机选A或者B，然后扔10次。以上步骤重复5次。

如果知道每次选的是A还是B，那可以直接估计（见下图a）。
如果不知道选的是A还是B（隐变量），只观测到5次循环共50次投币的结果，这时就没法直接估计A和B的正面概率。EM算法此时可起作用（见下图b）。

抛两枚硬币模型的python实现

具体参考这里：

对于第一次的抛，测试输出是否和论文一致：

# 硬币投掷结果观测序列
observations = np.array([[1, 0, 0, 0, 1, 1, 0, 1, 0, 1],
                         [1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
                         [1, 0, 1, 1, 1, 1, 1, 0, 1, 1],
                         [1, 0, 1, 0, 0, 0, 1, 1, 0, 0],
                         [0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])
                         
coin_A_pmf_observation_1 = stats.binom.pmf(5,10,0.6)
coin_B_pmf_observation_1 = stats.binom.pmf(5,10,0.5)

normalized_coin_A_pmf_observation_1 = coin_A_pmf_observation_1/(coin_A_pmf_observation_1+coin_B_pmf_observation_1)

# 更新在当前参数下A、B硬币产生的正反面次数
counts['A']['H'] += weight_A * num_heads
counts['A']['T'] += weight_A * num_tails
counts['B']['H'] += weight_B * num_heads
counts['B']['T'] += weight_B * num_tails

# 在初始化的theta下，AB分别产生正反面的次数被估计出来了
# 可以基于结果更新theta了
new_theta_A = counts['A']['H'] / (counts['A']['H'] + counts['A']['T'])
new_theta_B = counts['B']['H'] / (counts['B']['H'] + counts['B']['T'])
# new_theta_A=0.713
# new_theta_B=0.581
# 是和论文一致的

完整的模型：

def em_single(priors, observations):
    """
    EM算法单次迭代
    Arguments
    ---------
    priors : [theta_A, theta_B]
    observations : [m X n matrix]
 
    Returns
    --------
    new_priors: [new_theta_A, new_theta_B]
    :param priors:
    :param observations:
    :return:
    """
    counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}}
    theta_A = priors[0]
    theta_B = priors[1]
    # E step
    for observation in observations:
        len_observation = len(observation)
        num_heads = observation.sum()
        num_tails = len_observation - num_heads
        contribution_A = stats.binom.pmf(num_heads, len_observation, theta_A)
        contribution_B = stats.binom.pmf(num_heads, len_observation, theta_B)   # 两个二项分布
        weight_A = contribution_A / (contribution_A + contribution_B)
        weight_B = contribution_B / (contribution_A + contribution_B)
        # 更新在当前参数下A、B硬币产生的正反面次数
        counts['A']['H'] += weight_A * num_heads
        counts['A']['T'] += weight_A * num_tails
        counts['B']['H'] += weight_B * num_heads
        counts['B']['T'] += weight_B * num_tails
    # M step
    new_theta_A = counts['A']['H'] / (counts['A']['H'] + counts['A']['T'])
    new_theta_B = counts['B']['H'] / (counts['B']['H'] + counts['B']['T'])
    return [new_theta_A, new_theta_B]
    
def em(observations, prior, tol=1e-6, iterations=10000):
    """
    EM算法
    :param observations: 观测数据
    :param prior: 模型初值
    :param tol: 迭代结束阈值
    :param iterations: 最大迭代次数
    :return: 局部最优的模型参数
    """
    import math
    iteration = 0
    while iteration < iterations:
        new_prior = em_single(prior, observations)
        delta_change = np.abs(prior[0] - new_prior[0])
        if delta_change < tol:
            break
        else:
            prior = new_prior
            iteration += 1
    return [new_prior, iteration]

# 调用EM算法
print em(observations, [0.6, 0.5])
# [[0.79678875938310978, 0.51958393567528027], 14] # 这个结果与论文一致

参考

If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/EM.html

Previous: K-近邻算法

Next: Think Stats: distribution calculation