分布的运算：

1. 偏度（skewness）是度量分布函数不对称程度的统计量。负的偏度表示分布向左偏（skews left），此时分布函数的左边会比右边延伸得更长；正的偏度表示分布函数向右偏。
2. 判断偏度另一方法：比较均值和中位数的大小。
3. 乌比冈湖效应（Lake Wobegon effect）：虚幻的优越性（ illusory superiority），是指人们通常会觉得自己各方面的能力都比社会上的平均水平高的一种心理倾向。
4. 基尼系数（Gini coefficient）是一个衡量收入不平衡程度的指标。
5. 随机变量（random variable）：代表产生随机数的过程。
6. 累计分布函数：CDFX(x)=P(X≤x)，随机变量X小于等于x的概率。
7. 概率密度函数（probability density function，PDF）：累积分布函数的导数。表示的不是概率，而是概率密度。因为其求导的来源是累计分布，表示某个数值点上概率的密度大小，而不是直接的概率值的大小。衡量：x轴上每个单位的概率。通过数值积分，可计算变量X在某个区间的概率。
8. 卷积：PDFZ=PDFY∗PDFX，两个随机变量的和的分布就等于两个概率密度的卷积。卷积不是直接概率密度的相乘，是去所有值的积分。
9. 正太分布的性质：对线性变换和卷积运算是封闭的（closed）。线性：\(\begin{align} X ~ (\mu, \sigma), X1 = aX + b => X1 ~ (a\mu+b, a^2\sigma) \end{align}\)​​。
10. 中心极限定理（Central Limit Theorem）：如果将大量服从某种分布的值加起来，所得到的和会收敛到正态分布。条件：1）用于求和的数据必须满足独立性；2）数据必须服从同一个分布；3）这些数据分布的均值和方差必须是有限的；4）收敛的速度取决于原来分布的偏度：指数分布很快收敛，对数正太分布，收敛速度慢。
11. 分布函数之间的关系：

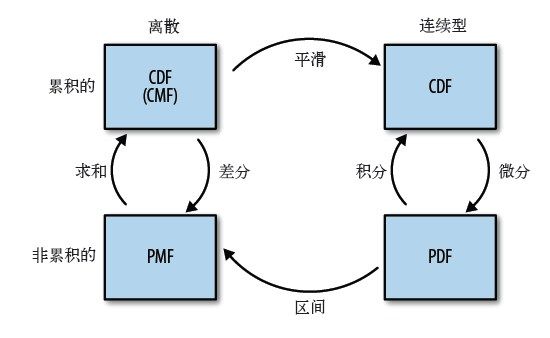
术语：

• 中心极限定理（Central Limit Theorem）** 早期的统计学家弗朗西斯·高尔顿爵士认为中心极限定理是“The supreme law of Unreason”。
• 卷积（convolution） 一种运算，用于计算两个随机变量的和的分布。
• 虚幻的优越性（illusory superiority） 心理学概念，是指人们普遍存在的将自己高估的一种心理。
• 概率密度函数（probability density function） 连续型累积分布函数的导数。
• 随机变量（random variable） 一个能代表一种随机过程的客体。
• 随机数（random variate） 随机变量的实现。
• 鲁棒性（robust） 如果一个统计量不容易受到异常值的影响，我们说它是鲁棒的。
• 偏度（skewness） 分布函数的一种特征，它度量的是分布函数的不对称程度。