概述
- 搜索引擎自动补全查询项,查看互联网上的用词来找出频繁的项集以作推荐。
- FP-growth:
- 高效(比Apriori快2个数量级)发掘频繁项集,不能用于发现关联规则
-
对数据集进行两次扫描,Apriori会对每个潜在的都进行扫描
- 基本过程:
- (1)构建FP树
- (2)从FP树中挖掘频繁项集
- FP(frequent pattern)树:
- FP-growth算法将数据存储在FP树中
- 一个元素项可以在FP树中出现多次
- 每个项集以路径的方式存储在树中,项集的出现频率也被记录
- 具有相似元素的集合会共享树的一部分
-
节点链接(node link):相似项之间的链接,用于快速发现相似项的位置
- 构建包含两步(两次扫描):
- 1)第一次扫描统计各item出现的频率,保留支持度在给定阈值以上的,得到频率表(header table)
- 2)将数据按照频率表进行重新排序:是每个item内的排序,此时哪些支持度低的就直接被丢掉了
- 3)二次扫描,构建FP树
- 从FP树挖掘频繁项集:
- 3个步骤:
- 1)从FP树获得条件模式基
- 2)利用条件模式基,构建条件FP树
-
3)重复迭代前两步,直到树包含一个元素项为止
- 条件模式基(conditional pattern base):以所查找元素项为结尾的路径集合,每一条路径是一条前缀路径(prefix path)。
-
前面已经有了频率表在头指针表中,可从这里的单个频繁元素项开始
- 创建条件FP树:
- 1)找到某个频繁项集的条件模式基
- 2)去掉支持度小于阈值的item
-
3)用这些条件基(路径前缀)构建条件树
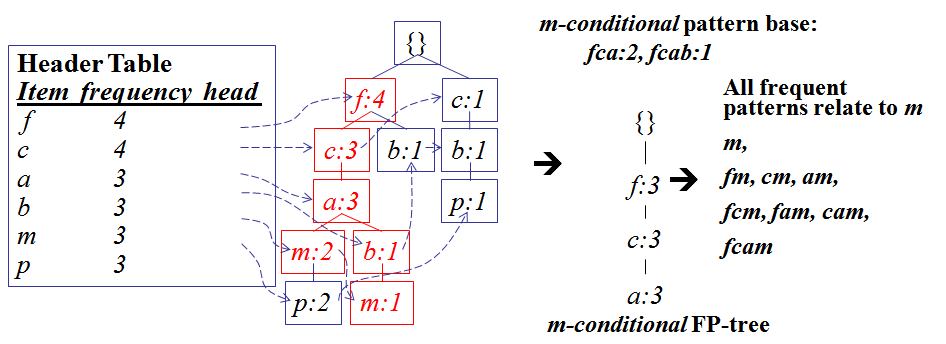
- 下图是对于上面数据中的m构建的条件FP树:
- 对于m含有的项包含3个({f,c,a,m,p}, {f,c,a,b,m}, {f,c,a,m,p}),
- 所以其条件基有3项({f,c,a,p}, {f,c,a,b}, {f,c,a,p}),
- 去掉支持度小于3的item,得到3项({f,c,a}, {f,c,a,b}, {f,c,a}),
- 所以其条件基为:fca:2, fcab:1(数值代表次数)。
- 类似的,上面是找的频繁集
m的条件树,可以再构建am,cm等的条件树,就能知道不同的组合的频繁集: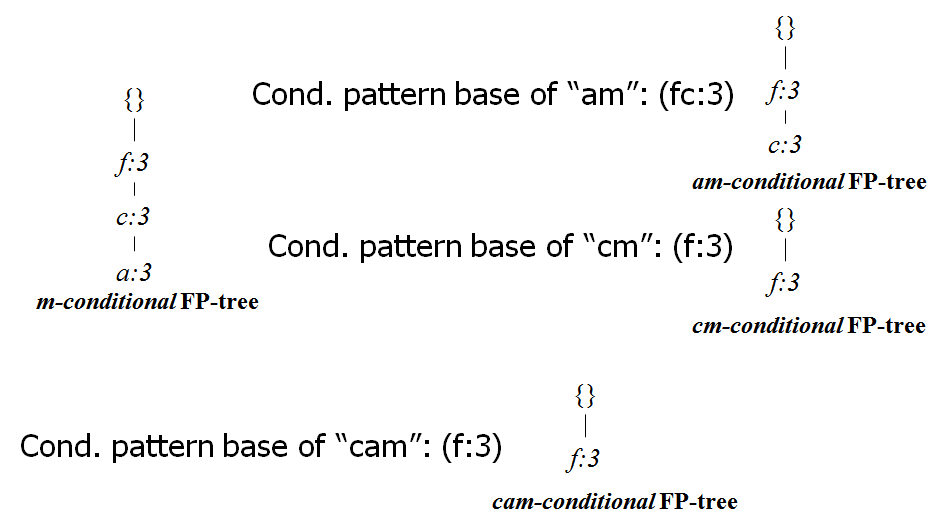
实现
Python源码版本
FP树构建:
class treeNode:
def __init__(self, nameValue, numOccur, parentNode):
self.name = nameValue
self.count = numOccur
self.nodeLink = None
self.parent = parentNode #needs to be updated
self.children = {}
def inc(self, numOccur):
self.count += numOccur
def disp(self, ind=1):
print ' '*ind, self.name, ' ', self.count
for child in self.children.values():
child.disp(ind+1)
def createTree(dataSet, minSup=1): #create FP-tree from dataset but don't mine
headerTable = {}
#go over dataSet twice
for trans in dataSet:#first pass counts frequency of occurance
for item in trans:
headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
for k in headerTable.keys(): #remove items not meeting minSup
if headerTable[k] < minSup:
del(headerTable[k])
freqItemSet = set(headerTable.keys())
#print 'freqItemSet: ',freqItemSet
if len(freqItemSet) == 0: return None, None #if no items meet min support -->get out
for k in headerTable:
headerTable[k] = [headerTable[k], None] #reformat headerTable to use Node link
#print 'headerTable: ',headerTable
retTree = treeNode('Null Set', 1, None) #create tree
for tranSet, count in dataSet.items(): #go through dataset 2nd time
localD = {}
for item in tranSet: #put transaction items in order
if item in freqItemSet:
localD[item] = headerTable[item][0]
if len(localD) > 0:
orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)]
updateTree(orderedItems, retTree, headerTable, count)#populate tree with ordered freq itemset
return retTree, headerTable #return tree and header table
从条件树挖掘频繁项集:
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])]#(sort header table)
for basePat in bigL: #start from bottom of header table
newFreqSet = preFix.copy()
newFreqSet.add(basePat)
#print 'finalFrequent Item: ',newFreqSet #append to set
freqItemList.append(newFreqSet)
condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
#print 'condPattBases :',basePat, condPattBases
#2. construct cond FP-tree from cond. pattern base
myCondTree, myHead = createTree(condPattBases, minSup)
#print 'head from conditional tree: ', myHead
if myHead != None: #3. mine cond. FP-tree
#print 'conditional tree for: ',newFreqSet
#myCondTree.disp(1)
mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
pyfpgrowth版本
python的模块pyfpgrowth可以很友好的进行频繁项集挖掘:
import pyfpgrowth
transactions = [[1, 2, 5],
[2, 4],
[2, 3],
[1, 2, 4],
[1, 3],
[2, 3],
[1, 3],
[1, 2, 3, 5],
[1, 2, 3]]
# find patterns in baskets that occur over the support threshold
patterns = pyfpgrowth.find_frequent_patterns(transactions, 2)
# find patterns that are associated with another with a certain minimum probability
# 所以这个是可以发掘规则的。。?
rules = pyfpgrowth.generate_association_rules(patterns, 0.7)
新闻网站点击流中的频繁项集:
gongjing@hekekedeiMac ..eafileSyn/github/MLiA/source_code/Ch12 (git)-[master] % head kosarak.dat
1 2 3
1
4 5 6 7
1 8
9 10
11 6 12 13 14 15 16
1 3 7
17 18
11 6 19 20 21 22 23 24
1 25 3
import fpGrowth
parsedData = [line.split() for line in open('kosarak.dat').readlines()]
parsedData[0:2]
# [['1', '2', '3'], ['1']]
initSet = fpGrowth.createInitSet(parsedData)
myFPtree, myHeaderTab = fpGrowth.createTree(initSet, 100000)
myFreqList = []
fpGrowth.mineTree(myFPtree, myHeaderTab, 100000, set([]), myFreqList)
len(myFreqList)
# 9
myFreqList
# [set(['1']), set(['1', '6']), set(['3']), set(['11', '3']), set(['11', '3', '6']), set(['3', '6']), set(['11']), set(['11', '6']), set(['6'])]
import pyfpgrowth
patterns = pyfpgrowth.find_frequent_patterns(parsedData, 100000)
len(patterns)
# 8
patterns
# {('3', '6'): 265180, ('11', '3', '6'): 143682, ('6',): 601374, ('11', '3'): 161286, ('1', '6'): 132113, ('1',): 197522, ('3',): 450031, ('11', '6'): 324013}
# 这个相比上面的结果少了一个:set(['1'])
参考
- 机器学习实战第12章
- FP-Growth Algorithm
If you link this blog, please refer to this page, thanks!
Post link:https://tsinghua-gongjing.github.io/posts/FP-growth-frequent-items.html
Previous:
Apriori关联分析
Next:
利用SVD简化数据
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me