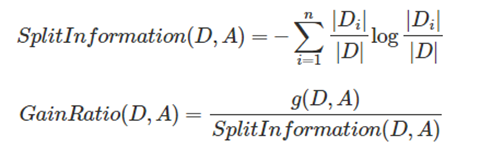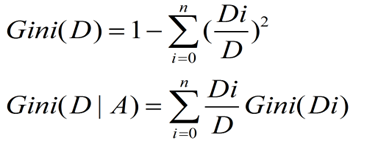决策树算法

Home > MachineLearning > Main text

Tag: python, machine learning

2018-07-28

概述

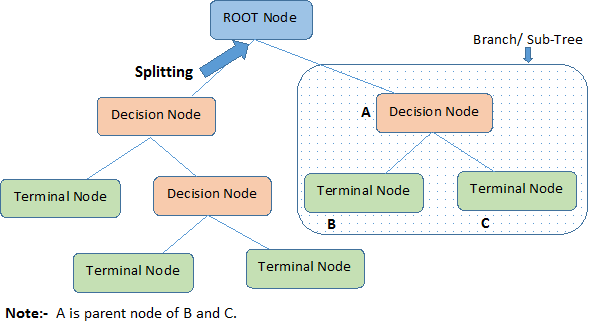
决策树算法：由一个决策图和可能的结果（包括资源成本和风险）组成，用来创建到达目标的规划。

决策树流程图

判断模块（decision block/node）
终止模块（terminating block/node）：已得出结论，可终止运行
分支（branch/sub-tree）：从判断模块引出的左右箭头

建树步骤

决策树的构建通常包含3个步骤：

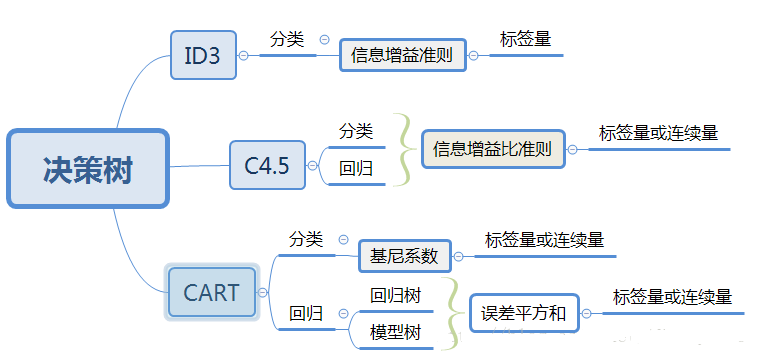
【1 特征选择】：选择什么特征进行分支，不同的算法采用不同的度量策略，比如ID3是基于信息增益最大的特征，C4.5则采用信息增益比，CART使用GINI系数
【2 生成决策树】：从从上至下递归的分支生成子节点
【3 剪枝】：决策树容易过拟合，所以需要缩小数的规模

建树的具体过程：

将所有的特征看成一个一个的节点（每次都是选取一个特征进行判断从而分支）；
遍历每个特征，进行分割计算，计算每个特征划分前后的信息增值（比如熵值之差）。选取最好的特征（增益最大的、熵值最小的）进行分割，从而将数据划分为不同的子节点；
对子节点分别递归执行上一步，直到每个最终的子节点都足够’纯’或者都属于同一类别为止。
递归结束条件：1）遍历完所有的属性，2）每个分支下的所有实例归属同一类。

如何选取划分特征？

ID3

信息增益(Information Gain)：划分数据集之前之后信息发生的变化，比如可以看熵值的变化，在每一个状态时具有一个熵值。

信息和熵值(Entropy)(参见下图的上半部分)：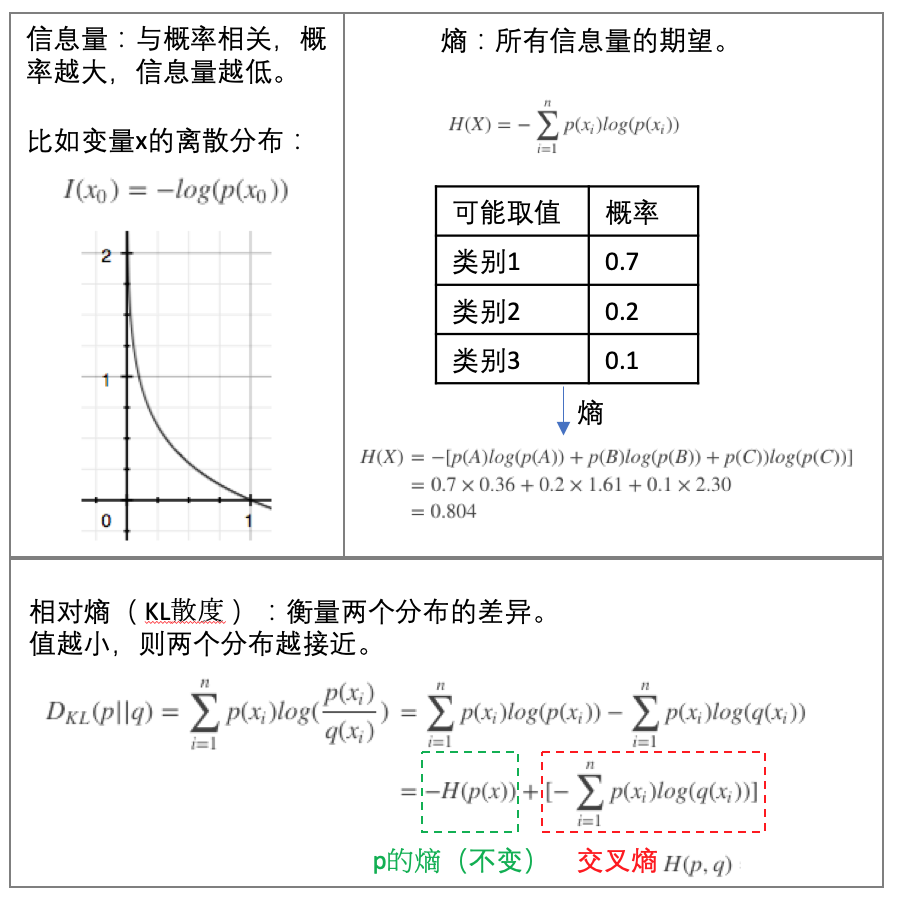

具体的计算如下：

下面是一个例子，比较不同的特征进行数据分隔时的信息增益大小：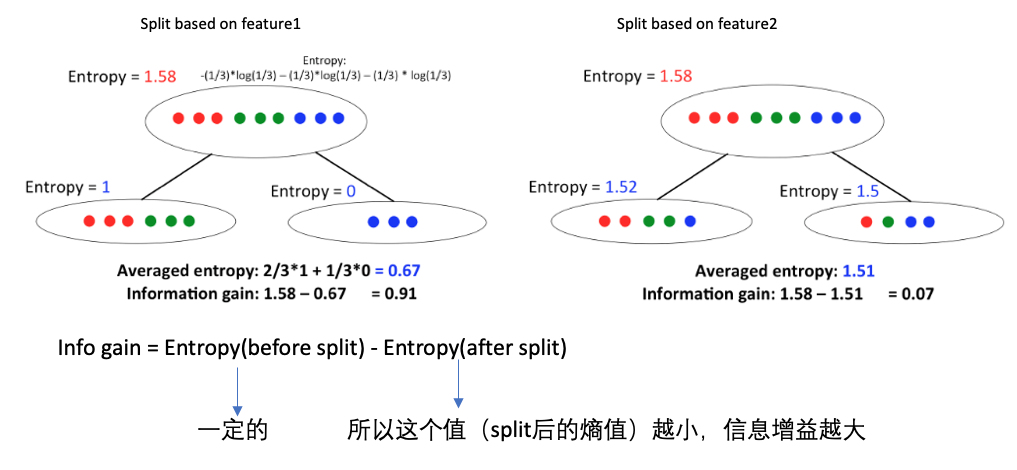

C4.5

ID3使用信息增益最大的特征作为分隔特征，这个对于特征是有偏向性的，具有多个值的特征其信息增益也容易大从而被选做分隔特征。为了消除这个，在C4.5中引入了信息增益比：

先计算某特征对于数据集的切割信息
然后用信息增益对于上述的切割信息进行归一化

CART

ID3和C4.5构建的树规模较大，为了提高建树的效率，CART方法被开发出来，其使用的是GINI系数来知道特征的选择：

三种算法的比较：

损失函数

在经典的ID3中，每次选取的分隔特征都是信息增益最大的，这个可以保证最后的分类效果达到最好，其损失函数值也是最小的。具体的，其损失函数很像最大似然估计函数：

实现

Python源码版本

计算给定数据集的香秾熵值：1）统计数据集label的count数，2）转换为概率，3）概率乘以对数概率并加和：

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet: #the the number of unique elements and their occurance
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) #log base 2
    return shannonEnt

划分数据集：对于给定的数据集，循环其每一个特征，计算特征对应的香农熵，选取其中熵值最小（信息增益最大）的特征作为划分的特征：

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):        #iterate over all the features
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
        uniqueVals = set(featList)       #get a set of unique values
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy
        if (infoGain > bestInfoGain):       #compare this to the best gain so far
            bestInfoGain = infoGain         #if better than current best, set to best
            bestFeature = i
    return bestFeature                      #returns an integer

sklearn版本

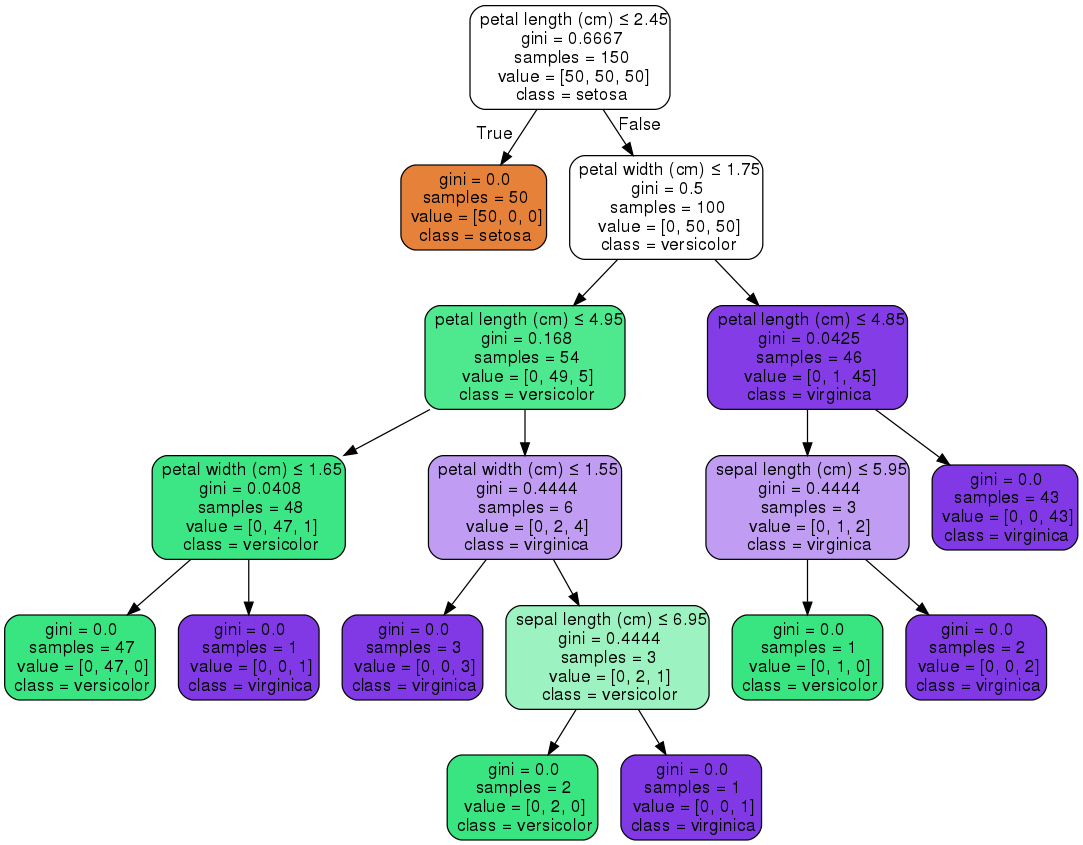
对于iris数据集应用决策树，过程中会搜索选取不同的特征及其阈值，以作为分隔的特征（节点）：

from sklearn.datasets import load_iris
from sklearn import tree

# Load in our dataset
iris_data = load_iris()

# Initialize our decision tree object
classification_tree = tree.DecisionTreeClassifier()

# Train our decision tree (tree induction + pruning)
classification_tree = classification_tree.fit(iris_data.data, iris_data.target)

import graphviz 
dot_data = tree.export_graphviz(classification_tree, out_file=None, 
                     feature_names=iris.feature_names,  
                     class_names=iris.target_names,  
                     filled=True, rounded=True,  
                     special_characters=True)  
graph = graphviz.Source(dot_data)  
graph.render("iris") 

参考

If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/decision_tree.html

Previous: Think Stats: distribution calculation

Next: 随机森林