• 背包问题：穷举算法
• 背包问题：动态规划
  • 构建网格
  • 填充行
• 背包问题FAQ
  • 再增加一个商品，需要重新构建网格吗？
  • 沿着列往下走，最大价值可能降低吗？
  • 行的顺序发生变化，结果会变吗？
  • 可以逐列而不是逐行填充吗？
  • 增加一个重量更小的商品有影响吗？
  • 可以偷取商品的一部分吗？
  • 旅游行程最优化
  • 处理相互依赖的情况
  • 计算最终的解时会设计两个以上的子背包吗？
  • 最优解可能导致背包没装满吗？
• 参考

背包问题：穷举算法

• 问题：偷取物品价值最高，如何选择？
• 简单算法：穷举
  • 3件商品：8种组合，选取最小的
  • 4件商品：16种组合，选取最小的
  • 5件商品：32种组合，选取最小的
  • 32件商品：40种组合，选取最小的
  • 每增加一件商品，需计算的集合数将翻倍
  • 算法时间：O(2^n)

背包问题：动态规划

• 原理：先解决子问题，再逐步解决大问题
• 背包问题：先解决小背包问题，再逐步解决原来的问题
• 下面是具体的流程：

构建网格

• DP都是从网格开始
• 最初是空的，就是通过填充网格，拿到最终解
• 填充是按照行开始的，一行一行的填充

填充行

• 行：表示当前的最大价值，当前所有物品+可选容积所决定
• 吉他行：
  • 物品：目前只有吉他可供选择
  • 实施：在对应容积（列）限制下，使得对应单元格价值最大，应该如何偷取？
  • 结果：现在只有吉他，且重量为1，在1-4之间，都偷取吉他达到单元格最大
• 音响行：
  • 物品：吉他+音响
  • 实施：在对应容积（列）限制下，使得对应单元格价值最大，应该如何偷取？
  • 结果1：更新单元格1，此前最大是吉他(1500)，现在可选的有音响(3000,4磅)，但是容积超过限制，因此不能偷取。
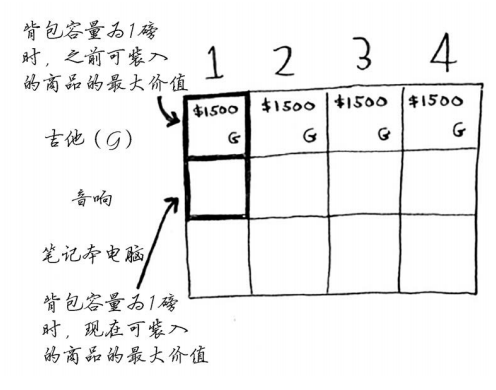
  • 结果2-3：同样的，可以偷取音响，但是容积不够，因此保持偷取原来最大的
  • 结果4：现在容积到达4，满足音响的，因此可以偷取音响，且价值高于原来的只偷取吉他，因此更新此处的偷取策略和价值
• 笔记本行：
  • 物品：吉他+音响+笔记本
  • 实施：在对应容积（列）限制下，使得对应单元格价值最大，应该如何偷取？
  • 结果1-2：小于2的时候，只能偷取1磅的吉他，保持偷吉他1500不变
  • 结果3：3磅的时候，满足可以偷取2000的笔记本，因此更新
  • 结果4：4的情形
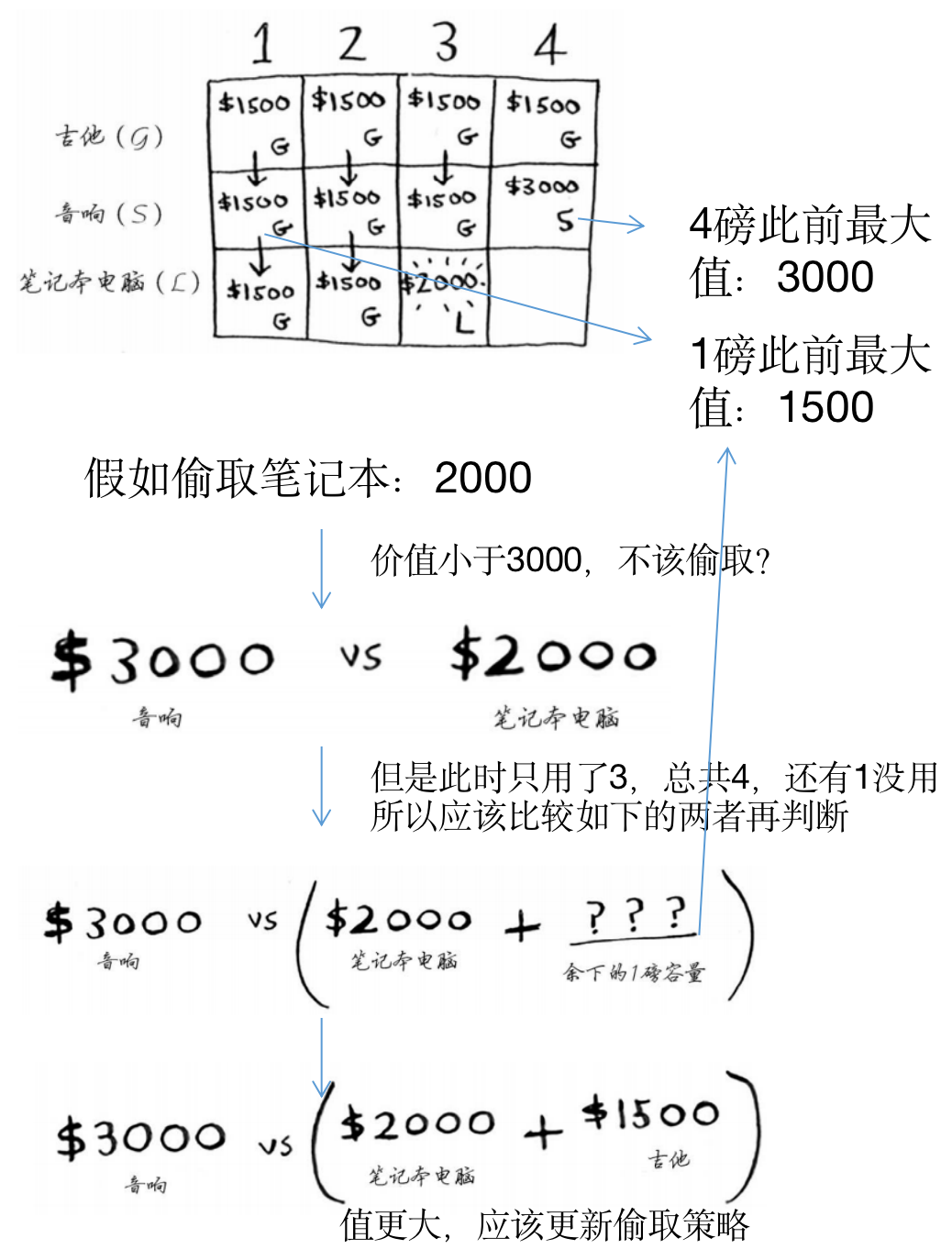
  • 从这里可以看到，为什么前面需要计算小背包时，能够获取的最大价值
• 填充公式：

背包问题FAQ

再增加一个商品，需要重新构建网格吗？

• 不用，本身DP就是逐步计算最大价值
• 可直接在原始网格后面，再添加一行新的物品，填充行

沿着列往下走，最大价值可能降低吗？

• 不会
• 每次迭代时，存储的都是当前的最大值，当新的值更小时，会保持这个最大值；当新的值更大时，会更新这个最大值，所以不可能比以前低。

行的顺序发生变化，结果会变吗？

• 不会有变化
• 各行的排列顺序无关紧要

可以逐列而不是逐行填充吗？

• 可以
• 就背包问题，逐列填充没有影响
• 但对于其他问题，可能有影响

增加一个重量更小的商品有影响吗？

• 需要重新构建粒度更细的网格
• 比如总共4，有一个0.5的项链，如果偷取项链，那么剩余3.5的最大价值是多少，之前的表格是不知道的，因此需要调整网格

可以偷取商品的一部分吗？

• 比如：有大米和扁豆，可打开包装，各偷取部分
• 不行。DP考虑的是要么拿走整件，要么不拿的情况，不能判断该不该拿商品的一部分。
• 其他方案：贪婪算法，先尽可能多的拿价值最高的，再次高的，等等

旅游行程最优化

• 前面的旅游问题可用DP方案
• 约束条件：有限的时间
• 单元格：整体的评分最大化
• 行：每个不同的城市景点

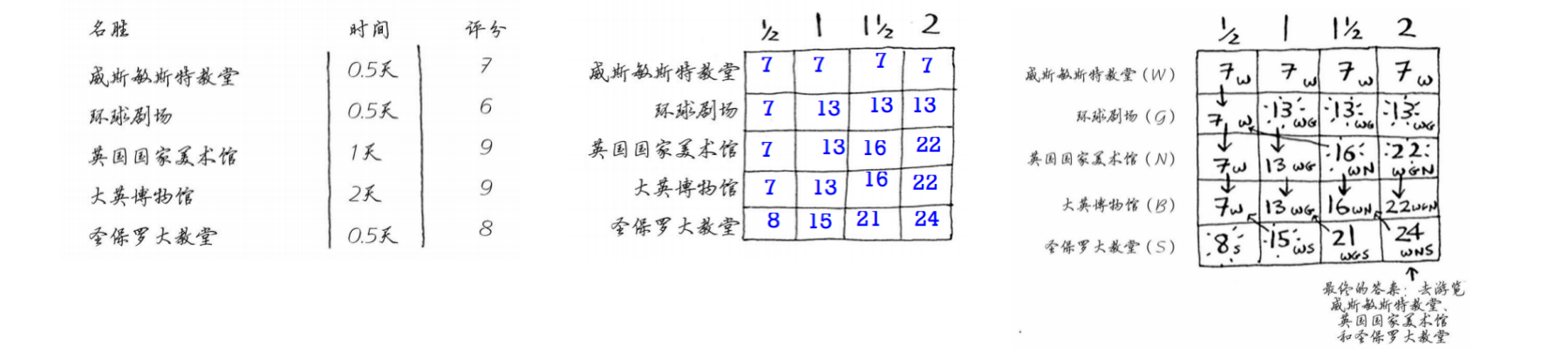
处理相互依赖的情况

• 比如在上面的形成增加了三个在巴黎的景点？是否可以DP？
• 不行。因为这三个地点在一起，是相互依赖的，当你到了其中一个之后，其他两个的时间是改变的。
• 仅当每个子问题都是离散的，即不依赖于其他子问题时，DP才管用。

计算最终的解时会设计两个以上的子背包吗？

• 不会。
• 大问题切成两个小问题
• 只是小问题，又可以切成两个小问题，但是每一次只涉及两个。

最优解可能导致背包没装满吗？

• 完全可能
• 比如还有一个3.5磅的无价之宝，当然会偷取这个，还剩0.5装不下任何其他东西。

参考

• 图解算法第九章