• 贪婪算法
• 教室调度问题
• 背包问题
• 集合覆盖问题：暴力穷举
• 集合覆盖问题：贪婪算法
• NP完全问题
• 参考

贪婪算法

贪婪算法：

• 原理：
  • 每步都采取最优的做法。比如下面的教室调度例子中，每次选择结束最早的课。
  • 即：每步都选择局部最优解，最终得到的就是全局最优解
• 优点：简单易行

教室调度问题

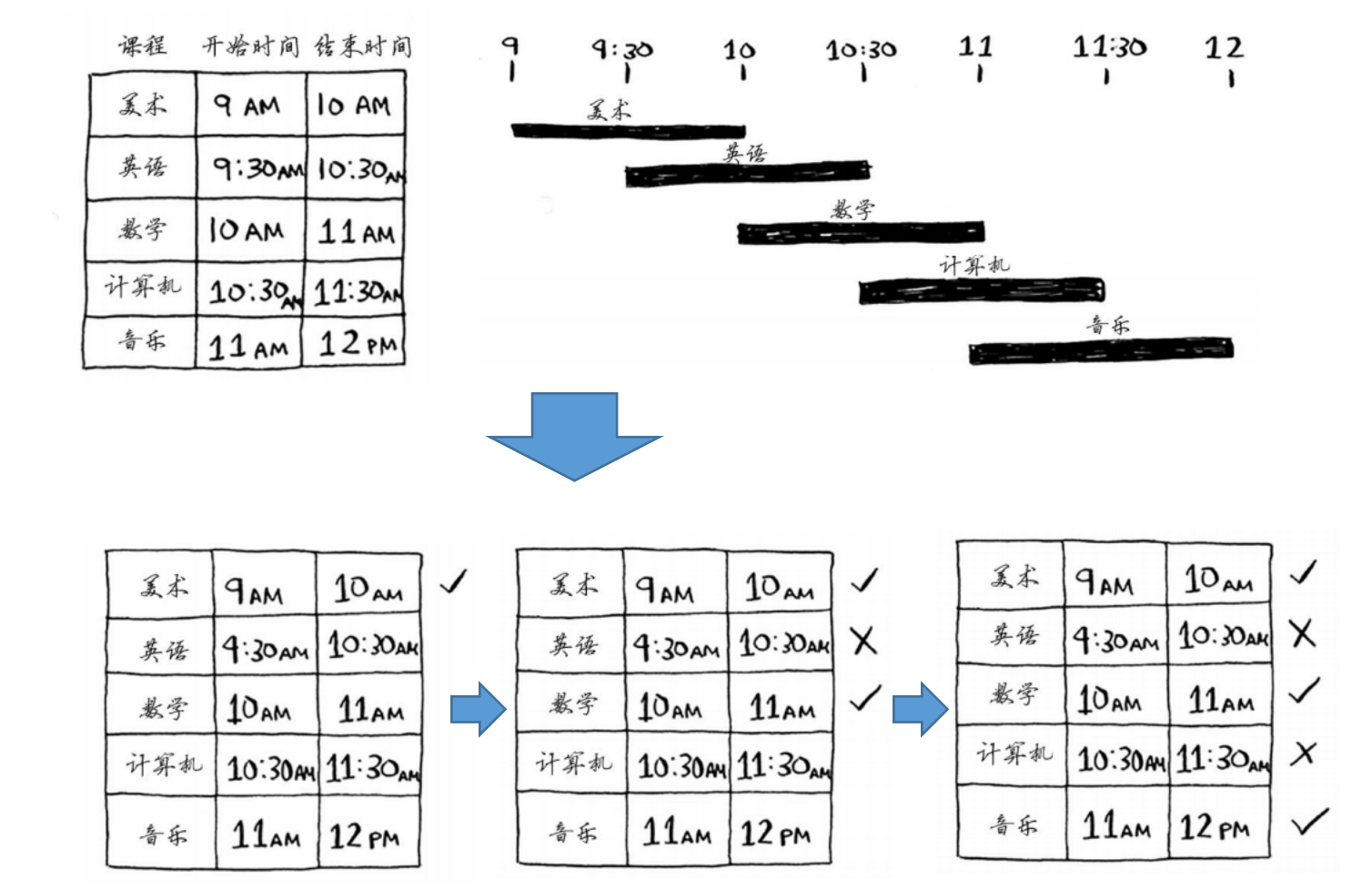
• 问题：给定一系列的课程上课时间，如何安排使得尽可能多的课程在同一个教室上？
• 解法：贪婪算法
  • 1）选出结束最早的课，设置为在教室上的第一堂课
  • 2）接下来，必须选择第一堂课上完之后才开始上的课，且是结束的最早的
  • 3）接下来，选择上堂课上完之后才开始上的课，且是结束的最早的
  • 4）重复。

背包问题

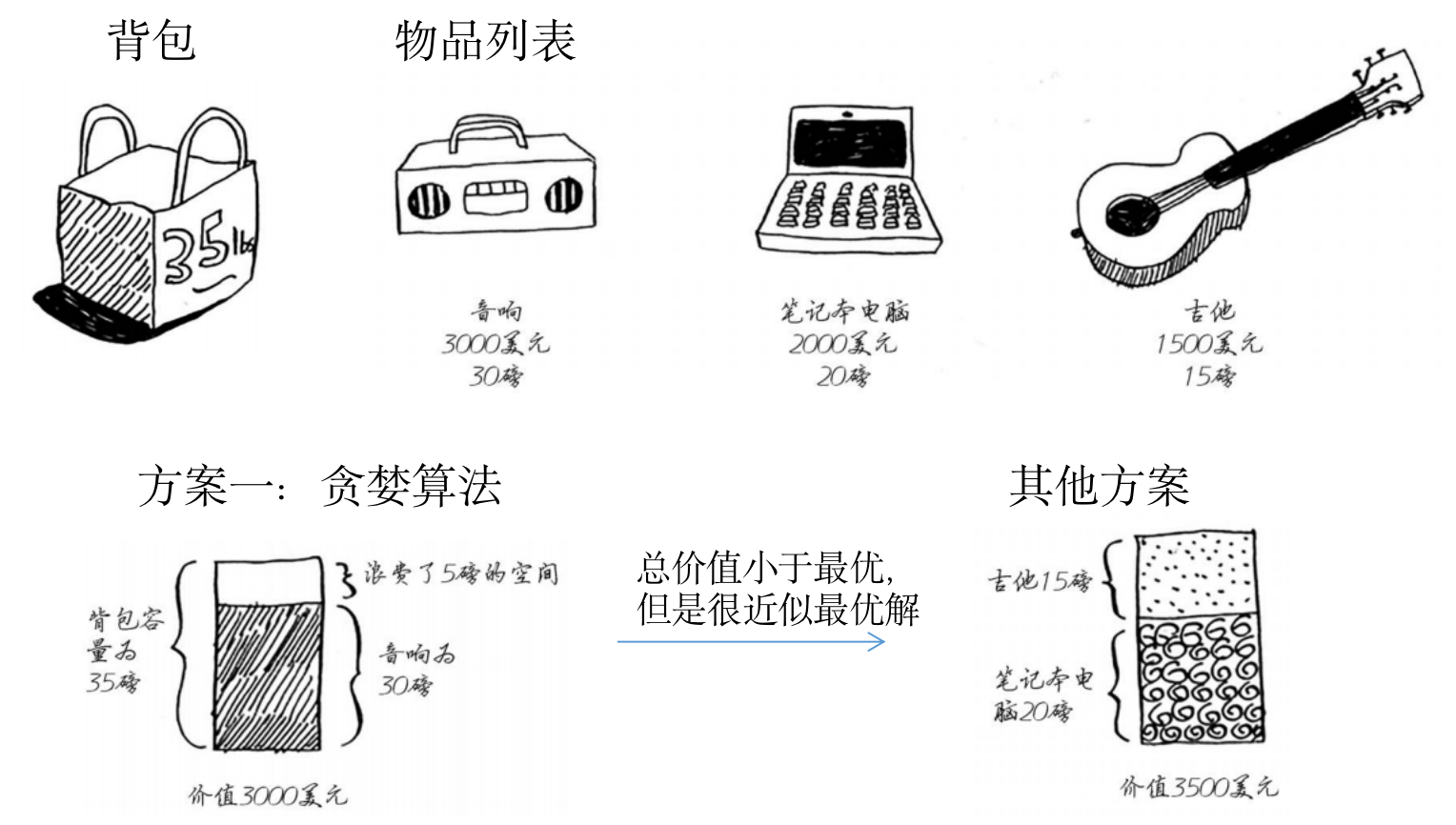
• 问题：一个贪婪的小偷，想在机场偷取物品放在自己的背包中，偷得物品总重量不超过背包可装重量35磅，每个物品均有对应价值，如何偷取使得价值最大？
• 贪婪解法：
  • 1）偷取可装入背包的最贵商品
  • 2）再偷取还可装入的最贵商品

  • 3）依次类推，直到装不下

  • 注意：
  • 贪婪策略虽然不能获得最优解，但是非常接近
  • 有些情况下，完美是优秀的敌人
  • 有时只需找到一个能大致解决问题的算法，而贪婪算法正好可以派上用场

集合覆盖问题：暴力穷举

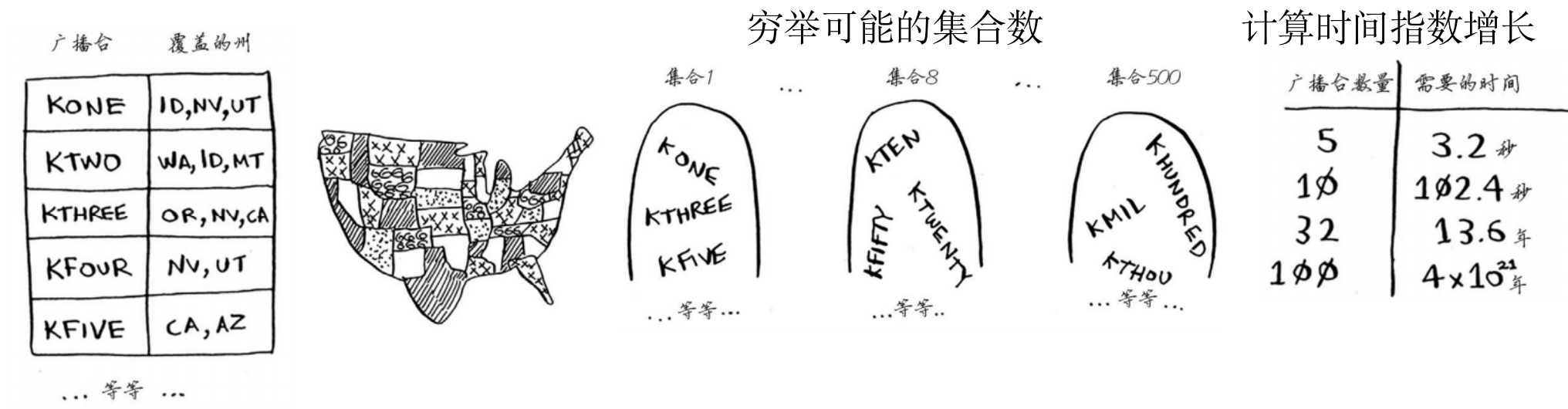
• 问题：一系列电台，每个电台只能在几个州收听到，如何选取最少的电台，使得能覆盖所有的州？
• 暴力解法：
  • 1）列出每个可能的电台集合，这里有2^n种，n是电台的总数
  • 2）从上述集合中，选出覆盖全美所有州的最小集合
  • 问题：
  • 随着电台数目的增加，集合数呈现指数上升（时间复杂度：2^n）
• 没有任何算法可以足够快的解决此问题

集合覆盖问题：贪婪算法

• 什么是近似算法：
  • approximation algorithm
  • 在获得精确解需要太长时间时，可使用近似
  • 近似算法的优劣判断：
    • 速度有多快
    • 得到的近似解与最优解的接近程度
• 贪婪算法：
  • 1）选出1个电台，其覆盖了最多的未覆盖的州
  • 2）重复第一步，直到所有的州都被覆盖
  • 时间复杂度：O(n^2)
• 实现：
  • 1）准备
    • 要覆盖集合：存储要覆盖的州。比如这里是所有的州
    • 电台字典。每个电台覆盖哪些州，州也用集合的形式给出。
    • 最终电台集合。存储最终选择的电台，动态变化，一步步添加，知道全部州被覆盖。
  • 2）循环
    • 当要覆盖集合不为空时，不断挑选电台
      • 挑选最好的电台，即覆盖未被覆盖的州数目最多的电台。
      • 最好电台加入到最终电台集合
      • 要覆盖集合中删除被此最好电台覆盖的电台

# You pass an array in, and it gets converted to a set.
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"])

stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])

final_stations = set()

while states_needed:
  best_station = None
  states_covered = set()
  for station, states_for_station in stations.items():
    covered = states_needed & states_for_station
    if len(covered) > len(states_covered):
      best_station = station
      states_covered = covered

  states_needed -= states_covered
  final_stations.add(best_station)

print(final_stations)

NP完全问题

定义：以难解著称的问题。需要计算所有的解，从中选出最小、最短的那个，比如旅行商问题或者集合覆盖问题

如何识别？

• 元素较少时算法的运行速度非常快，但是随着元素数量的增加，速度会变得非常慢
• 通常是：
  • 涉及“所有组合”的问题
• 可能是：
  • 不能将问题分成小问题，必须考虑各种可能的情况
  • 问题涉及序列（如旅行商问题的城市序列）且难以解决
  • 问题涉及集合（如电台集合）且难以解决
• 肯定是：
  • 问题可转换为集合覆盖问题或者旅行商问题

例子：

• 有个邮递员负责给20个家庭送信，需要找出经过这20个家庭的最短路径。请问这是一个NP完全问题吗？【是的，都需要送到，旅行商问题】
• 在一堆人中找出最大的朋友圈（即其中任何两个人都相识）是NP完全问题吗？【是的，需要穷举不同的集合，挑选出两两认识最多的那个集合】
• 你要制作美国地图，需要用不同的颜色标出相邻的州。为此，你需要确定最少需要使用多少种颜色，才能确保任何两个相邻州的颜色都不同。请问这是NP完全问题吗？【我不确定。答案：是的】

参考

• 图解算法第八章