目录

• 目录
• bagging和决策树
• 随机森林：bagging+决策树
• 随机森林：决策树结构的多样性
• Out-Of-Bag(OOB) 估计：大约1/3的样本没有涵盖
• OOB vs validation：类似的效果验证
• 特征选择
  • 含义
  • 优缺点
  • 特征筛选：基于权重计算
  • 随机森林的特征选择和效果评估
• sklearn调用
• 参考

bagging和决策树

• bagging：通过bootstrap的方式，从原始数据集D得到新的数据集D‘，然后对每个得到的数据集，使用base算法得到相应的模型，最后通过投票形式组合成一个模型G，即最终模型。
• 决策树：通过递归，利用分支条件，将原始数据集D进行切割，成为一个个的子树结构，到终止形成一棵完整的树形结构。最终的模型G是相应的分支条件和分支树递归组成。

随机森林：bagging+决策树

• 是bagging和决策树的结合

• bagging：减少不同数据集对应模型的方差。因为是投票机制，所以有平均的功效。
• 决策树：增大不同的分支模型的方差。数据集进行切割，分支包含样本数在减少，所以不同的分支模型对不同的数据集会比较敏感，得到较大的方差。
• 结合两者：随机森林算法，将完全长成的CART决策树通过bagging的形式结合起来，得到一个庞大的决策模型。

• random forest(RF)=bagging+fully-grown CART decision tree

• 优点：
  • 效率高：不同决策树可以由不同主机并行训练生成
  • 继承了CART的优点

  • 将所有决策树通过bagging的形式结合起来，避免单个决策树造成过拟合

  • 在随机森林中，树的个数越多，模型稳定性表现越好
  • 实际应用中，尽可能选择更多的树
  • 可能与random seed有关：初始化值的影响

随机森林：决策树结构的多样性

获得不同的决策树的方式：

• 【1】随机抽取数据集。通过bootstrap得到不同的数据集D’，基于D‘构建模型
• 【2】随机抽取子特征。
  • 比如原来100个特征，只随机选取30个进行构建决策树

  • 每一轮得到的树由不同的30个特征构成，每棵树不一样

  • 类似d到d’维的特征转换，相当于从高维到低维的投影，也就是d‘维z空间是d维x空间的一个随机子空间（subspace）
  • 通常d’远小于d，算法更有效率
  • 此时的随机森林增加了random-subspace
  • RF=bagging+random-subspace CART
• 【3】现有特征的线性组合。
  • 现有特征x通过数组p的线性组合：\(\phi(x)=p_i^Tx\)
  • 可能很多特征的权重为0
  • 每次的分支不再是单一的子特征集合，而是子特征的线性组合
  • 二维平面：不止水平和垂直线，还有各种斜线

  • 选择的是一部分特征，属于低维映射

  • 随机森林算法又有增强
  • 从随机子空间增强到随机组合
  • 类似于perceptron模型
  • RF=bagging+random-combination CART

Out-Of-Bag(OOB) 估计：大约1/3的样本没有涵盖

• bagging：通过bootstrap抽取样本集D‘，但是有的样本是没有涵盖进去的
• out-of-bag (OOB) example：对每轮的抽取训练，没有被涵盖的样本
• 某个样本是某次抽取OOB的概率：\((1-\frac{1}{N})^N = \frac{1}{(\frac{N}{N-1})^N} = \frac{1}{(1+\frac{1}{N-1})^N} = \frac{1}{e}\)，其中e是自然对数，N是原本数据集数量
• 所以，在每个子模型g中，OOB数目大约是\(\frac{1}{e} \times N\)，即大约有1/3的样本此次没有被抽中

OOB vs validation：类似的效果验证

上面的bagging涉及到的bootstrap随机抽取数据集训练不同的模型的过程，是不是和交叉验证比较像，下表是两者选取数据集合训练的比较：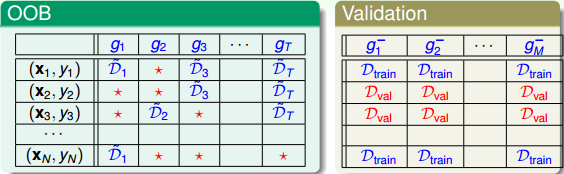

有几点值得注意：

• 验证表格中：蓝色是训练数据，红色是验证数据，两者没有交集
• OOB表格中：蓝色是训练数据，红色是OOB样本（约占1/3, \(\frac{1}{e}\)）

• OOB类似于验证数据集（都是未参与训练的），那么是否能用OOB验证构建的模型g的好坏呢？可以！

• 通常不验证单个g的好坏，只有组合的模型G表现足够好即可
• 问题转换：OOB验证g的好坏 =》OOB验证组合模型G的好坏
• 方法：
  • 对每个OOB，看其属于哪些（有的样本可能是多个D’的OOB，因为每一轮都有约1/3的样本是OOB）模型g的OOB样本
  • 计算这个OOB在这些g上的表现，求平均。

  • 例子：\((x_N,y_N)\)是\(g_2,g_3,g_T\)的OOB，那么\((x_N,y_N)\)在\(G_N^-(N)\)上的表现是：\(G_N^-(N)=average(g_2,g_3,g_T)\)

  • 这个做法类似于留一法验证，每次只对一个样本验证其在所属的所有的OOB的g模型上的表现（不是单个模型）

  • 计算所有的OOB的表现：
  • 平均表现：\(E_{oob}(G)=\frac{1}{N}\sum_{n=1}^Nerr(y_n,G_N^-(x_n))\)，这就是G的好坏的估计，称为bagging或者随机森林的self-validation。
  • self-validation相比validation优点：不需要重复训练。在validation中，选择了使得validation效果最好的数据集之后，还需要对所有的样本集进行训练，以得到最终模型。随机森林中得到最小的\(E_{oob}\)后，即完成了整个模型的建立。

特征选择

含义

特征选择：从d维特征到d‘特征的subset-transform，最终是由d’维特征进行模型训练。比如原来特征有10000个，选取300个，需要舍弃部分特征：

• 【1】冗余特征。重复出现，但是表达相似含义的，比如年龄和生日
• 【2】不相关特征。

优缺点

• 优点：
  • 提高效率，特征越少，模型越简单。
  • 正则化，防止特征过多出现过拟合。
  • 去除无关特征，保留相关性大的特征，解释性强。
• 缺点：
  • 特征筛选计算量大。
  • 不同的特征组合，也容易发生过拟合。
  • 容易选到无关特征，解释性差。

特征筛选：基于权重计算

筛选：计算每个特征的重要性（权重），再根据重要性的排序进行选择。

• 线性模型。容易计算，线性模型的加权系数就是每个特征的权重，所以加权系数的绝对值大小代表了特征的重要性。
• 非线性模型。难以计算，比如随机森林就是非线性模型，所以会有其他的方式进行特征选择。

随机森林的特征选择和效果评估

• 核心：random test
• 原理：对于某个特征，如果用一个随机值替代后表现比之前更差，则该特征很重要，权重应该大。（随机替代表现 =》重要性）
• 随机值选取：
  • 【1】使用均匀或者高斯分布随机抽取值

  • 【2】通过permutation方式，将原来的N个样本的第i个特征打乱（重新洗牌）

  • 方法【2】更科学，保证了特征分布是近似的
  • 【2】称为permutation test（随机排序测试）：在计算第i个特征的重要性的时候，将N个样本的第i个特征重新洗牌，然后比较\(D\)和\(D^{(p)}\)表现的差异性。如果差异很大，则表明第i个特征是重要的。
• 如何衡量表现？（因为是要看\(D\)和\(D^{(p)}\)表现的差异）
  • 之前介绍了\(E_{oob}(G)\)可以衡量，但是对于重新洗牌的数据\(D^{(p)}\)，要重新训练，且每个特征都要训练，在比较与原来的\(D\)的效果，繁琐复杂。
  • RF作者提出：把permutation的操作从原来的training上移到了OOB validation上去 \(E_{oob}(G^{(p)}) -> E_{oob}^{(p)}(G)\)
  • 具体：训练时使用D，在OOB验证时，将所有的OOB样本的第i个特征重新洗牌，验证G的表现。

sklearn调用

>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.datasets import make_classification

# 构建数据集
>>> X, y = make_classification(n_samples=1000, n_features=4,
...                            n_informative=2, n_redundant=0,
...                            random_state=0, shuffle=False)

# 构建分类器
>>> clf = RandomForestClassifier(n_estimators=100, max_depth=2,
...                              random_state=0)

# 模型训练
>>> clf.fit(X, y)  
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
            max_depth=2, max_features='auto', max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=None,
            oob_score=False, random_state=0, verbose=0, warm_start=False)
            
# 获得每个特征的重要性分数
>>> print(clf.feature_importances_)
[0.14205973 0.76664038 0.0282433  0.06305659]

# 预测新数据
>>> print(clf.predict([[0, 0, 0, 0]]))
[1]

参考

• Random Forest