Home > MachineLearning > Main text

判别生成模型、朴素贝叶斯、高斯判别分析

Tag: python, machine learning
2018-08-04

生成式模型 vs 判别式模型

对于监督学习，其最终目标都是在给定样本时，预测其最可能的类别，即优化目标总是：\(\begin{align}\arg \max_yp(y\|x)\end{align}\)。

求解上述优化目标总的可分为两类：

  • 判别式模型（Discriminant Model）：直接学习模型得到\(p(y\|x)\)，即根据数据集学习参数模型：\(p(y\|x; \theta)\)，那么在预测的时候直接根据新样本的x特征值计算y值（所属的类别的概率）。此类包含：1）线性回归模型，2）逻辑回归模型，3）决策树模型 等

  • wiki: a generative model is a model of the conditional probability of the observable X, given a target y, symbolically,{P(X|Y=y)}.

  • 生成式模型（Generative Model）：利用贝叶斯法则，对上述的优化目标进行转换。
  • wiki: a discriminative model is a model of the conditional probability of the target Y, given an observation x, symbolically,{P(Y|X=x)}
  • 贝叶斯公式: \(p(y\|x)=\frac {p(x,y)}{p(x)}=\frac {p(x\|y)p(y)}{p(x)}\)
  • 代入上面的优化目标：\(\begin{align}\arg \max_yp(y\|x)&=\arg \max_y\frac {p(x\|y)p(y)}{p(x)}\\&=\arg \max_yp(x\|y)p(y)\end{align} (给定数据x时，p(x)是常量可不考虑)\)
  • 此时模型的求解目标不是\(p(y\|x)\)，而是\(p(x\|y)\)和\(p(y)\)
  判别模型 生成模型
关注点 关注各类的边界 关注每一类的分布，不关注决策边界的位置
优点 1.能得到类之间的差异信息
2.学习简单		 1.研究类内部问题更加灵活
2.更适合增量学习
3.对数据不完整适应更好，更鲁棒
缺点 1.不能得到每一类的特征（可以告诉你的是1还是2，但是没有办法把整个场景描述出来）
2.变量关系不清晰、不可视		 1.学习计算相对复杂
2.更倾向于得到false positive，尤其是对比较近的事物分类（比如牛和马）
举例 LR、SVM、KNN、traditional neural network、conditional random field naive bayes、mixtures of mutinomial/gaussians/experts、HMMs、Sigmoidal belief networks、bayesian networks、markov random fields

例子

目标：判别一个动物是大象(y=1)还是狗(y=0)

判别式模型：

  • 【训练】考虑动物的所有特征，学习模式\(p(y\|x; \theta)\)
  • 【预测】基于学习的模型，判定是大象还是狗

生成式模型：

  • 【训练1】训练所有的类别为大象的数据，学习模型1：\(p(x\|y=1)和p(y=1)\)
  • 【训练2】训练所有的类别为狗的数据，学习模型2：\(p(x\|y=0)和p(y=0)\)
  • 【预测】用模型1和2分别预测，可能性大的即为最终的预测类别

高斯判别分析

高斯判别分析（Gaussian discriminant analysismodel, GDA）：

  • 用于连续空间，即随机变量具有连续值特征
  • 假设\(p(x\|y)\)是服从高斯分布的，这是一个概率分布 GDA.png

朴素贝叶斯

  • 用于学习离散值随机变量
  • 贝叶斯决策：选择具有最高概率的决策。对应于分类，即如果属于某一类别的概率是最大的，则分为该类别。
  • 朴素：分类器过程中只做最原始、最简单的假设
  • 条件概率：\({\displaystyle P(A\mid B)={\frac {P(B\mid A)P(A)}{P(B)}}}\)
    • P(A|B)是已知B发生后A的条件概率，即A的后验概率。
    • P(A)是A的先验概率
    • P(B|A)是已知A发生后B的条件概率，即B的后验概率。
    • P(B)是B的先验概率。

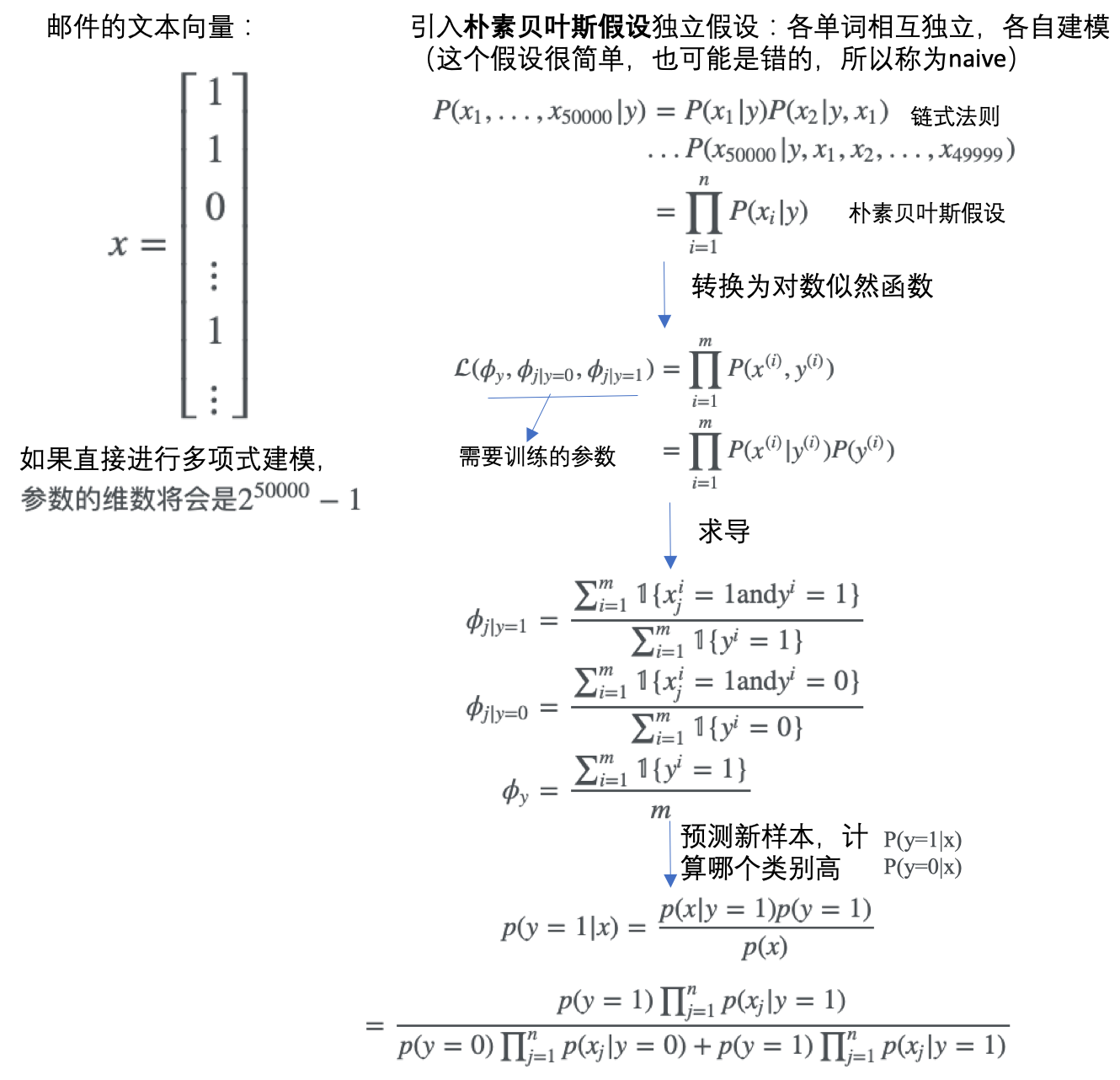
文本/邮件分类

  • 对于很多问题，比如邮件文本分类，如果直接进行多项式建模，那么参数空间会很大。所以引入朴素贝叶斯假设，认为单词之间是相互独立的，而通常这个假设是过于简单的、甚至是错的（too naive）。naive_bayes.png

对于上面的文本分类问题，涉及到具体的几个步骤：

1、数据准备：从文本构建词向量

  • 通过loadDataSet函数构建post文本内容及对应的标签（是否是侮辱性的）
  • 然后createVocabList函数基于所有的文档，提取所有唯一的单词集合
  • setOfWords2Vec函数基于单词集合，把输入的post文本转换为一个单词向量，长度和单词集合相等，出现某单词则值为1，未出现则为0
def loadDataSet():
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]    #1 is abusive, 0 not
    return postingList,classVec
                 
def createVocabList(dataSet):
    vocabSet = set([])  #create empty set
    for document in dataSet:
        vocabSet = vocabSet | set(document) #union of the two sets
    return list(vocabSet)

def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else: print "the word: %s is not in my Vocabulary!" % word
    return returnVec

2、模型训练：基于词向量计算概率

  • trainMatrix：词向量矩阵，每一行是一个文本，每一列表示某个单词在该文本中是否出现
  • trainCategory：文本所属的类别

根据这个函数，就可以计算出，在每个类别中每个单词出现的概率，具体这里是两个类别：侮辱性的（标记为1的）和非侮辱性的（标记为0的）。

def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pAbusive = sum(trainCategory)/float(numTrainDocs)
    p0Num = ones(numWords); p1Num = ones(numWords)      #change to ones() 
    p0Denom = 2.0; p1Denom = 2.0                        #change to 2.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = log(p1Num/p1Denom)          #change to log()
    p0Vect = log(p0Num/p0Denom)          #change to log()
    return p0Vect,p1Vect,pAbusive

注意：

  • p0Num = ones(numWords); p1Num = ones(numWords)这里的初始化可以初始化为全0矩阵，但是如果某个单词没有出现，其概率为0，最后的乘积也为0，所以可以初始化为全1矩阵；
  • p1Vect = log(p1Num/p1Denom)这里如果不取log，有可能由于太多的很小的数值相乘造成下溢出问题，所以去对数。

3、模型测试

根据训练数据，已经计算了每个类别中每个单词的出现频率。对于新的文本数据，就可以基于此来计算此文本属于每一个类别的概率，最后文本所属的类别就是概率值最大的那一类。因为这里引入了贝叶斯假设，认为不同的单词之间是相互独立的，所以可以直接计算得到概率，就是下面的vec2Classify * p1Vec和vec2Classify * p0Vec，vec2Classify就是待分类文本的词向量，p1Vec是类别1中单词的概率，两者元素相乘再加和就是文本属于类别1的概率。

def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)    #element-wise mult
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else: 
        return 0
      
def testingNB():
    listOPosts,listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat=[]
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb)
    testEntry = ['stupid', 'garbage']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb)

词集模型 vs 词袋模型

  • 词集模型（set-of-words model）：所有单词只唯一的计数，每个单词只出现一次
  • 词袋模型（bag-of-words model）：每个单词可出现多次，次数越多，则在文档中出现的概率越大
# 词集模型
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else: print "the word: %s is not in my Vocabulary!" % word
    return returnVec
    
# 词袋模型
def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] += 1
    return returnVec

sklearn版本

参考这里的文档:

# load data
from sklearn.datasets import fetch_20newsgroups
twenty_train = fetch_20newsgroups(subset='train',
    categories=categories, shuffle=True, random_state=42)
    
# Tokenizing text
from sklearn.feature_extraction.text import CountVectorizer
count_vect = CountVectorizer()
X_train_counts = count_vect.fit_transform(twenty_train.data)

# occurrences to frequencies
tfidf_transformer = TfidfTransformer()
X_train_tfidf = tfidf_transformer.fit_transform(X_train_counts)

# train NB model
from sklearn.naive_bayes import MultinomialNB
clf = MultinomialNB().fit(X_train_tfidf, twenty_train.target)

# test model
docs_new = ['God is love', 'OpenGL on the GPU is fast']
X_new_counts = count_vect.transform(docs_new)
X_new_tfidf = tfidf_transformer.transform(X_new_counts)

predicted = clf.predict(X_new_tfidf)

for doc, category in zip(docs_new, predicted):
    print('%r => %s' % (doc, twenty_train.target_names[category]))

联合成一个pipeline：

# training
from sklearn.pipeline import Pipeline
text_clf = Pipeline([
    ('vect', CountVectorizer()),
    ('tfidf', TfidfTransformer()),
    ('clf', MultinomialNB()),
])
text_clf.fit(twenty_train.data, twenty_train.target) 

# testing
import numpy as np
twenty_test = fetch_20newsgroups(subset='test',
    categories=categories, shuffle=True, random_state=42)
docs_test = twenty_test.data
predicted = text_clf.predict(docs_test)
np.mean(predicted == twenty_test.target)

参考


If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/discriminant-generative-bayes-gaussian.html
Previous: 随机森林

    Category

    Latest articles

    Links