Home > MachineLearning > Main text

模型评估与选择

Tag: python, machine learning
2018-10-05

目录

经验误差与过拟合

  1. 错误率（error rate）：分类错误的样本数占样本总数。m个样本中有a个分类错误：\(E = \frac{a}{m}\)
  2. 精度（accuracy）：1-错误率，\(1-\frac{a}{m}\)
  3. 误差（error）：模型的实际预测输出与样本的真实输出之间的差异。
    • 训练集：训练误差（training error），或经验误差（empirical error）
    • 新样本：泛化误差（generalization error）
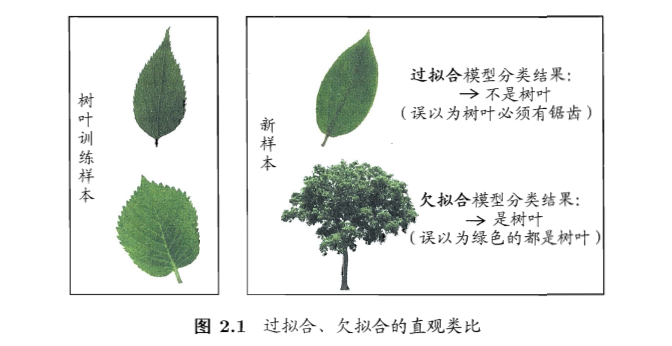
  4. 过拟合（overfitting）：把训练样本学习得太好了，训练样本自身的一些特点当做了所有潜在样本都有的一般性质，泛化性能下降
    • 无法彻底避免，只能缓解或者减小风险
    • 为啥不可避免？面临的问题通常是NP难，有效算法是在多项式时间内运行完成，如可彻底避免过拟合，意味着构造性的证明“P=NP”，所以不可避免
  5. 欠拟合（underfitting）：对训练样本的一般性质尚未学好 overfitting_underfitting.png

模型评估方法

  1. 一般用一个测试集测试模型在新样本上的效果，用这个测试误差去近似泛化误差。
  2. 一个数据集如何训练与测试？
  3. 留出法（hold-out）：
    • 数据集D划分为互斥的两个集合，训练集S，测试集T
    • S上训练模型，T上测试模型，其测试误差用于近似泛化误差
    • 注意：训练、测试集的划分要尽可能保持数据分布的一致性，避免引入额外误差。类似于分层采样（stratified sampling）：保持样本的类别比例。
    • 注意：需要若干次随机划分、重复进行实验，以多次结果的平均值作为留出法的结果。
    • 问题：希望评估数据集D（所有数据）训练出的模型。S大T小，则评估结果不够稳定准确；S小T大，则训练的模型与真实的存在大的差别，降低了保真性（fidelity）。
    • 常见做法：约2/3-4/5用于训练，其余用于测试
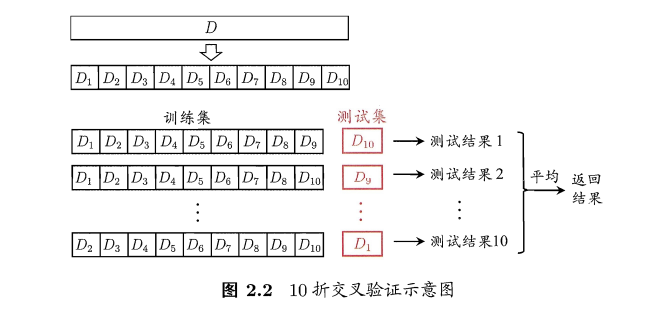
  4. 交叉验证法（cross validation）：
    • 数据集D通过分层采用划分为k个互斥的子集，每次用k-1个训练，其余1个测试
    • k个测试结果的均值
    • k大小：决定了模型的稳定性和保真性，又称为k折交叉检验（k-fold cross validation）
    • k常用的是10，还有5、20等
    • 划分有多种方式，存在随机性，所以需要重复p次，比如“10次10折交叉检验”
    • 留一法（leave-one-out）：令k=m，即每个样本看为一个子集。每次的训练集仅比真实数据集D少1，模型很保真。数据量大时，训练m个模型的计算和时间开销太大。kfold_cross_validation.png
  5. 自助法（bootstrapping）：
    • 留出法、交叉验证：样本规模不一样导致的估计偏差

    • 留一法：计算复杂度太高

    • 基于自助采样（bootstrap sampling）：每次随机挑选一个，放回再随机抽取，重复m次，获得和样本数目相同的抽样样本。
    • 有的样本出现多次，有的一次不出现。
    • 样本在m次抽样中始终不被采到的概率：\((1 - \frac{1}{m})^m\)，对其求取极限：\(=\frac{1}{e}=0.368\)，即约有36.8%的样本未出现在采样集合中。
    • 训练集：抽样样本，测试集：总体样本-抽样样本
    • 约1/3没有用于测试，称为包外估计（out-of-bag estimate）
    • 应用场景：数据集小、难以有效区分训练/测试集时；生成多个不同训练集，利于集成学习。在数据量足够时，留出法和交叉验证更常用。
    • 改变了初始数据集分布，会引入估计偏差
  6. 调参与最终模型：
    • 选择算法
    • 对算法参数进行设定：参数调节（parameter tuning）
    • 通常：每个参数选定范围和变化步长

模型性能度量

  1. 性能度量（performance measure）：评价泛化能力
  2. 错误率和精度：上面已经介绍了
  3. 准确率（查准率，precision）：\(P = \frac{TP}{TP+FP}\)
  4. 召回率（查全率，recall）：\(R = \frac{TP}{TP+FN}\)
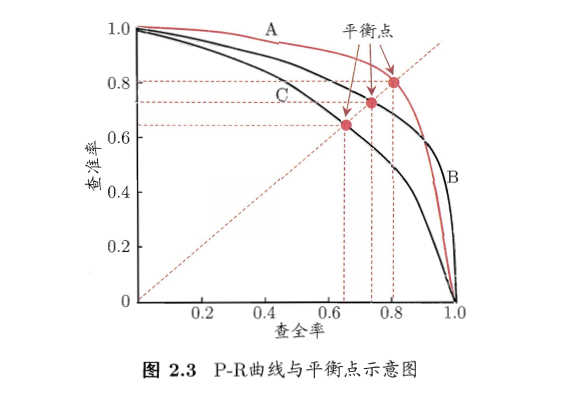
  5. 基于准确率和召回率的PR曲线：
    • 直观显示模型在样本总体上的准确率和召回率
    • 一个包住另一个，则性能更优，比如下面的A优于C
    • 如果交叉，难以一般性判断，比如下面的A和B。看曲线下面积。
    • 平衡点（break-event point。BEP）：准确率=召回率的取值，综合反映性能优劣，越大则性能越好。比如下图中BEP（C）=0.64，BEP（A）=0.8，可认为A优于C。P-R-curve.png
  6. F1度量：
    • F1 score: \(F1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{样本总数 + TP - TN}\)
    • 不同情形下，对准确率和召回率重视程度不同，所以F1有更一般的形式：\(F_\beta = \frac{(1+\beta^2) \times P \times R}{(\beta^2 \times P) + R}\)。\(\beta=1\)，标准的F1；\(\beta>1\)，召回率更大影响；\(\beta<1\)，准确率更大影响。
  7. n个混淆矩阵上综合考察准确率和召回率：
    • 1）宏版本：
    • 在各混淆矩阵上分别计算出准确率和召回率：(P1,R1),(P2,R2),…,(Pn,Rn)，再计算平均值，得到：
    • 宏准确率：\(macro-P = \frac{1}{n}\sum_{i=1}^{n}P_i\)
    • 宏召回率：\(macro-R = \frac{1}{n}\sum_{i=1}^{n}R_i\)

    • 宏F1：\(macro-F1 = \frac{2 \times macro-P \times macro-R}{macro-P + macro-R}\)

    • 2）微版本：
    • 将各混淆矩阵的对应元素进行平均，得到TP、FP、TN、FN的平均值：\(\overline{TP}, \overline{FP}, \overline{TN}, \overline{FN},\)，再基于平均值计算，得到：
    • 微准确率：\(micro-P = \frac{\overline{TP}}{\overline{TP} + \overline{FP}}\)
    • 微召回率：\(micro-R = \frac{\overline{TP}}{\overline{TP} + \overline{FN}}\)
    • 微F1：\(micro-F1 = \frac{2 \times micro-P \times micro-R}{micro-P + micro-R}\)
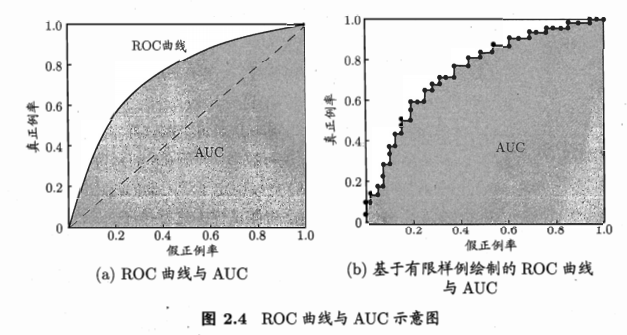
  8. ROC & AUC:
    • 模型：很多情况是预测一个实数概率值，与给定阈值进行比较，高则预测为正，低则预测为负。例子：神经网络，输出值与0.5比较
    • 根据测试排序，最前面则最可能是正，后面的最可能为负。排序质量的好坏，体现了泛化性能的好坏。
    • ROC（receiver operating characteristic，受试者工作特征）曲线：源于二战敌机雷达信号检测。基于预测结果进行排序，逐个把样本作为正例进行预测，计算两个量值，作为曲线的横纵坐标。
    • 纵轴：真正例率（True positive rate，TPR），\(TPR = \frac{TP}{TP+FN}\)
    • 横轴：假正例率（False positive rate，FPR），\(FPR = \frac{FP}{TN+FP}\)

    • 现实数据中，有限样本，曲线不能很平滑：ROC_AUC.png

    • AUC：曲线下面积，近似计算如下，\(AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)(y_i+y_{i+1})\)

偏差与方差

  1. 解释泛化性能：
    • 上面是估计的模型的泛化性能
    • 为什么是这样的性能？解释：偏差-方差分解（bias-variance decomposition）
  2. 偏差-方差分解：
    • 对学习算法的期望泛化错误率进行拆解
    • 例子：回归，
    • \[测试样本x\]
    • \[y_D为x在数据集中的标记\]
    • \[y为x的真实标记\]
    • \[f(x;D)为训练D上学习的模型f在x上的预测输出\]
    • 算法期望预测：\(\overline{f}(x)=E_D[f(x;D)]\)
    • 方差：\(var(x)=E_D[(f(x;D)-\overline{f}(x))^2]\)，同样大小的训练集的变动所导致的学习性能的变化，刻画了数据扰动所造成的影响。
    • 噪声：\(\epsilon^2=E_D[(y_D-y)^2]\)，当前任务上任何学习算法所能达到的期望泛化误差的下界，刻画了学习问题本身的难度。
    • 偏差（bias）：\(bias^2(x)=(\overline{f}(x)-y)^2\)，期望输出与真实标记的差别，学习算法的期望预测与真实结果的偏离程度，刻画了算法本身的拟合能力。

    • 期望泛化误差分解：\(E(f;D)=E_D[(f(x;D)-\overline{f}(x))^2] + (\overline{f}(x)-y)^2 + E_D[(y_D-y)^2]=var(x) + bias^2(x) + \epsilon^2\)，即为方差、偏差、噪声之和。

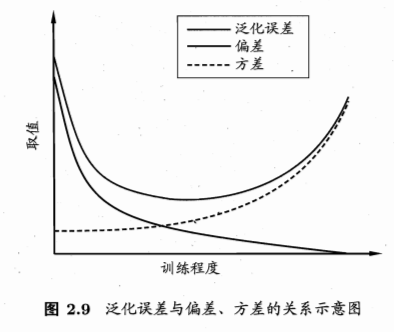
    • 偏差-方差窘境（bias-variance dilemma）：偏差与方差的冲突
    • 训练不足：拟合能力弱，训练数据的扰动不影响结果，偏差主导泛化错误率
    • 训练充足：拟合能力强，训练数据的轻微扰动被学习到，学习模型发生显著变化，过拟合，方差主导泛化错误率 bias_variance.png

参考


If you link this blog, please refer to this page, thanks!
Post link：https://tsinghua-gongjing.github.io/posts/model_evaluation_selection.html
Previous: sklearn: 缺失值插补

    Category

    Latest articles

    Links