目录

• 目录
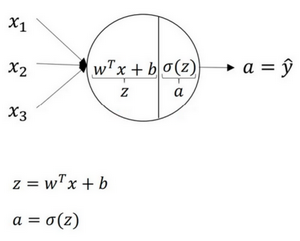
• 概述
• 神经网络表示
• 计算网络输出
• 向量化计算
• 激活函数
• 反向传播
• 随机初始化
• 参考

概述

• 逻辑回归神经元:
  • 输入特征，参数 =》计算z =》计算a =》 计算损失函数
• 神经网络：
  • 前向和后向传播

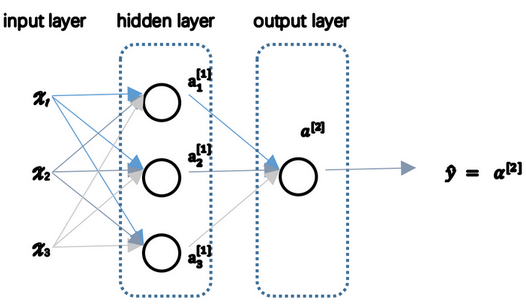
神经网络表示

• 输入层：神经网络的输入
• 隐藏层：在训练中，中间结点的准确值是不知道的，看不见它们在训练中具有的值，所以称为隐藏。
• 输出层：产生预测值
• 惯例：
  • 网络层数：输入层不算在内
  • 输入层：第零层

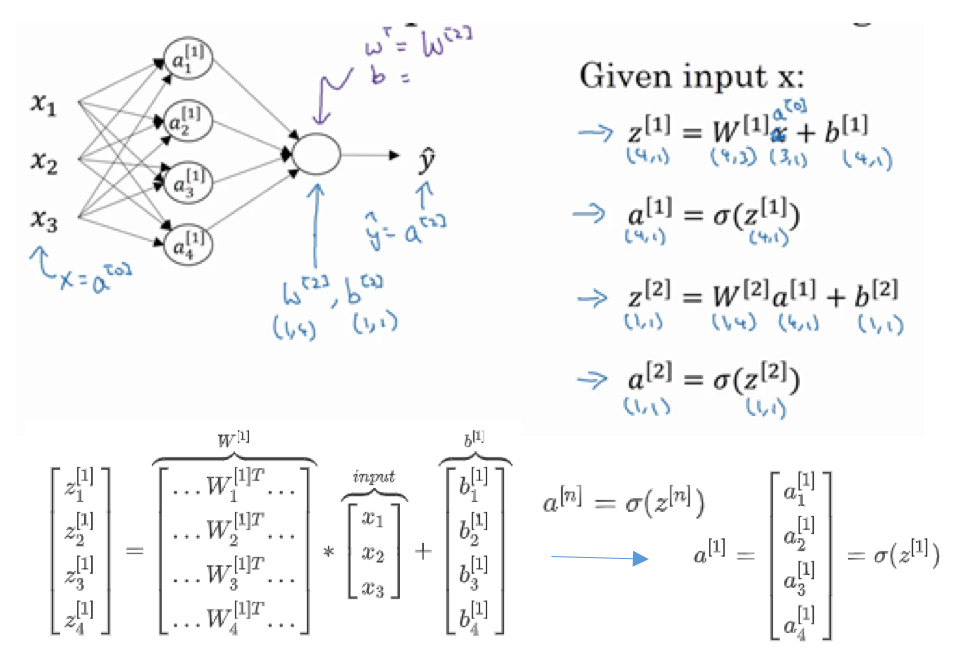
计算网络输出

• 逻辑回归神经元计算：
  • 计算z，在计算a
• 多层神经元：
  • 很多次上面的重复计算
  • 比如二层神经网络，前向计算第一层的z

向量化计算

• 单个样本：
• 多样本：
  • 所有样本都考虑，同时计算：

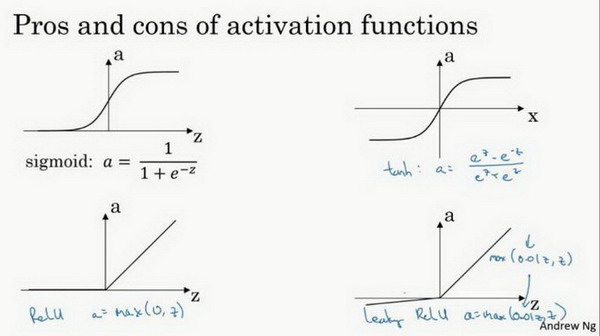
激活函数

• 通常情况：tanh函数或者双正切函数总体上都优于sigmoid函数
• tanh函数：是sigmoid函数向下平移和伸缩后的结果
• 优化算法说明：基本不用sigmoid函数，tanh函数在所有场合都优于sigmoid函数
  • 例外：二分类问题，输出层是0或者1，需要使用sigmoid函数
• 经验法则：
  • 如果输出是0、1值（二分类问题），则输出层选择sigmoid函数，然后其他的所有单元选择ReLU函数
• ReLU & leaky ReLU：
  • 更快。在z的区间变动很大时，激活函数斜率都大于0，而sigmoid函数需要进行size运算，所以前者效率更高。
  • 不会产生梯度弥散现象。sigmoid和tanh，在正负饱和区时梯度接近于0。
• 为什么要非线性激活函数：
  • 如果使用线性激活函数，神经网络只是对输入进行线性组合，不能构建复杂的模拟情况
  • 不能在隐藏层使用线性激活函数：用ReLU或者tanh等非线性激活函数
  • 唯一可用线性激活函数的：输出层
• 各激活函数的导数：

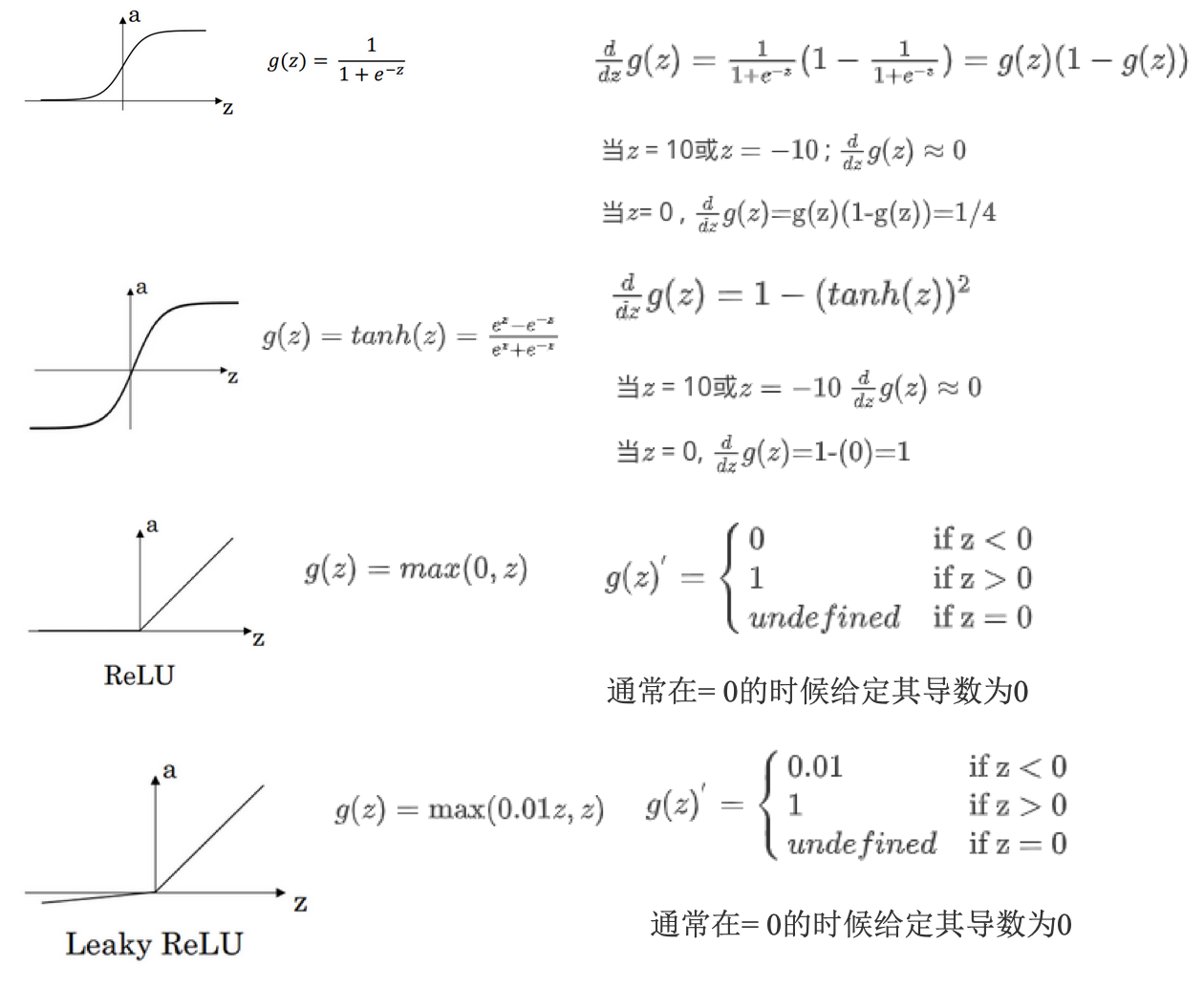
反向传播

• 逻辑回归的：
• 具体可参见另外一个例子：09: Neural Networks - Learning，这里有个例子说明了反向传播的计算的全过程。

随机初始化

• 逻辑回归：初始化权重可以为0
• 神经网络：初始化权重不能为0.
  • 如果设置为0，那么梯度下降将不起作用。
  • 所有隐含单元是对称的，无论运行梯度下降多久，都是计算同样的函数
  • 一般基于高斯分布随机生成一些数，再乘以一个很小的系数（比如0.01），作为初始值。

参考

• 第三周：浅层神经网络