Algorithm: 狄克斯特拉算法
2017-01-25
狄克斯特拉算法
- vs 广度优先搜索:
- BFS:寻找最短的段数的路径
- Dijkstra:带权重的图,找到加权最小的路径
- 步骤:
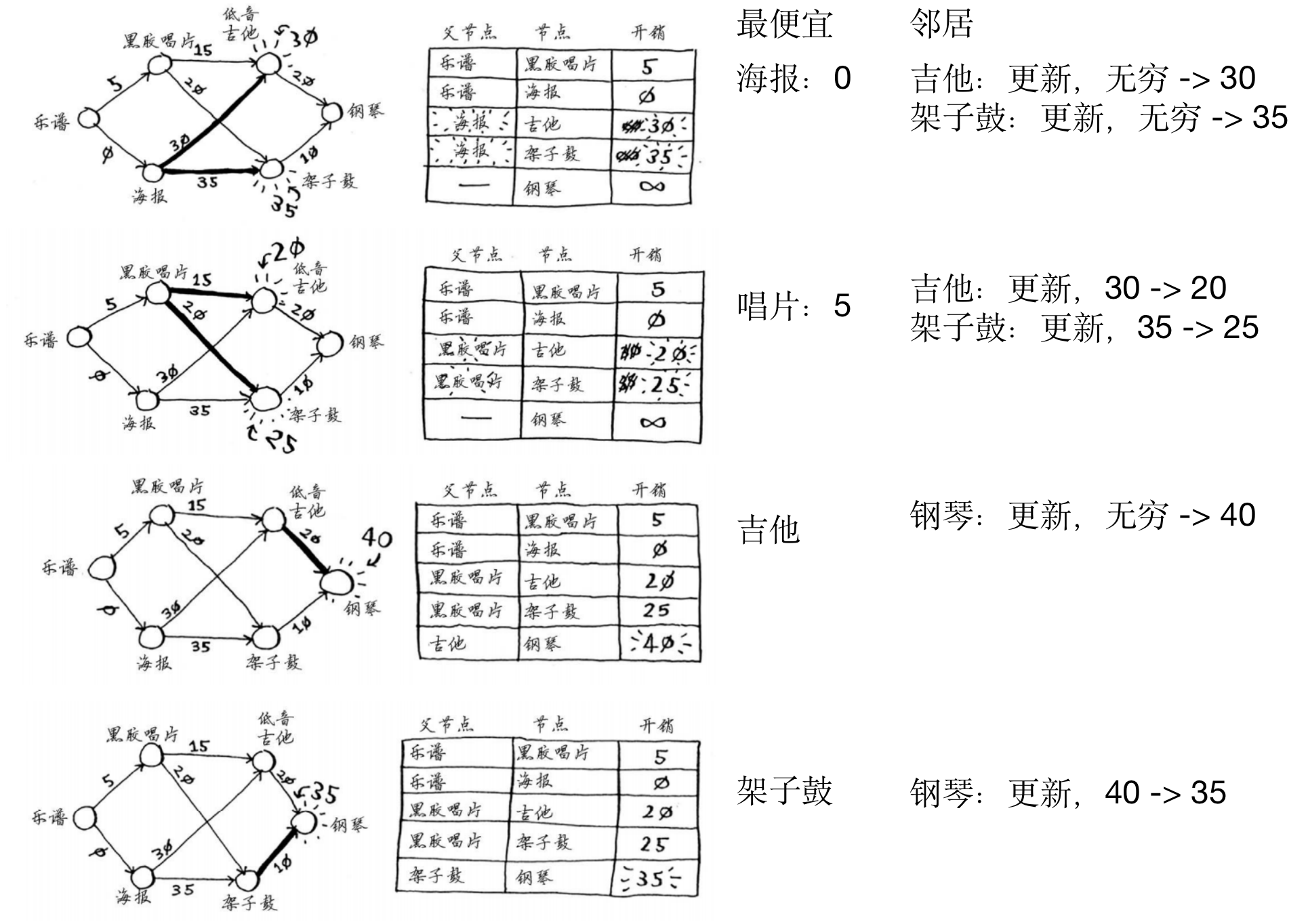
- 1)找出“最便宜”的节点,即可在最短时间到达的
- 2)更新该节点的邻居的开销。即如果有经过当前最便宜节点到达邻居节点的更小值,则更新邻居节点的开销。
- 3)重复上述过程,直到对图中的每个节点都这样做了
- 4)计算最终路径
- 例子:
- 下面是前三步确定到每个节点的最小距离

- 狄克斯特拉:总权重最小
- 广度优先搜索:段数最少
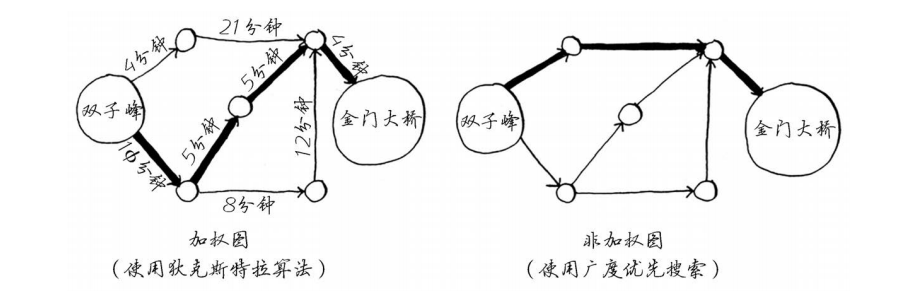
术语
- 权重:图中每条边有关的数字
- 加权图:weighted graph,带权重的图
- 最短路径:使用狄克斯特拉算法
- 非加权图:unweighted graph,不带权重的图
- 最短路径:使用广度优先搜索
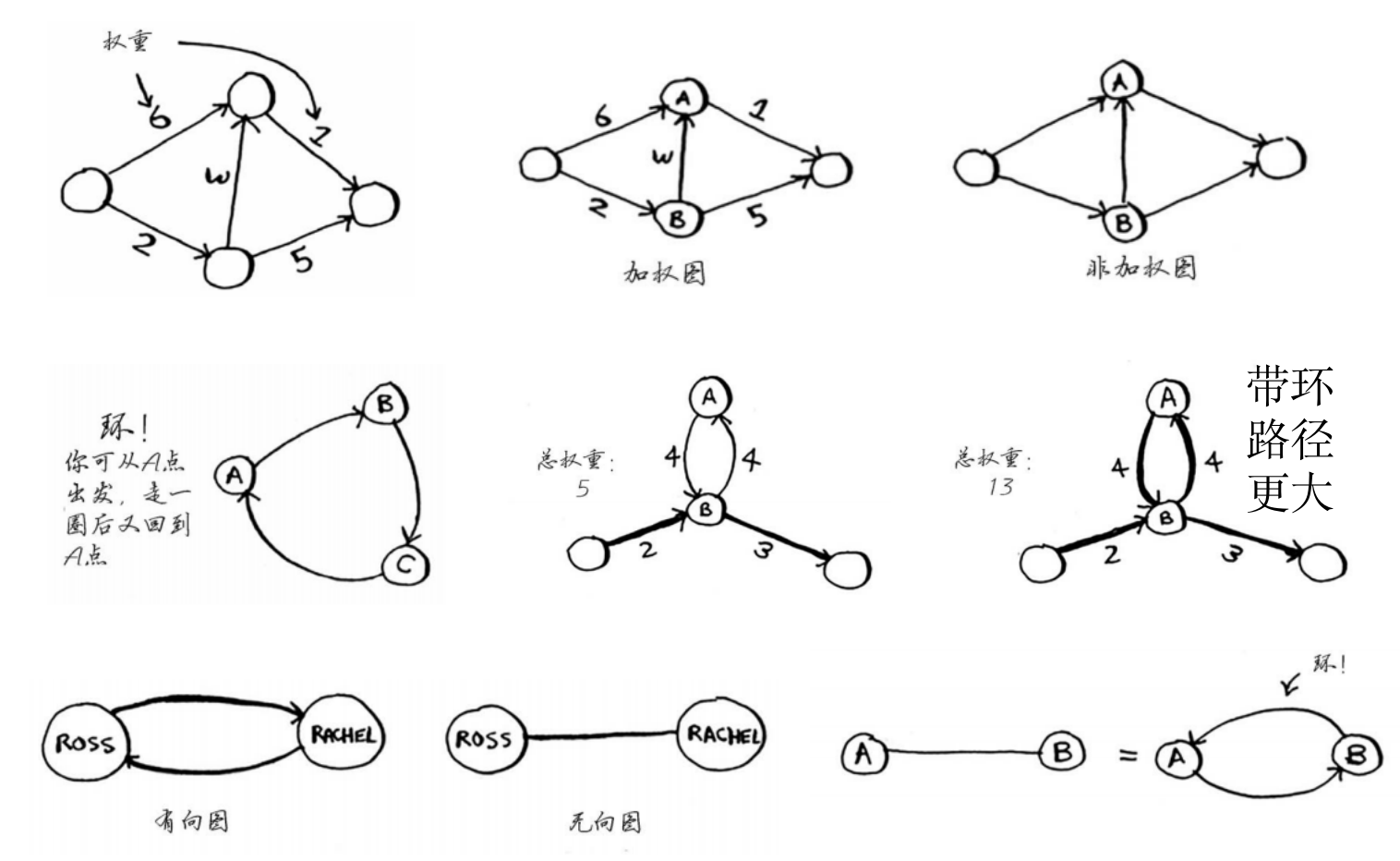
- 环:从某一点出发,又可以回到该点
- 绕环的路径增加了权重
- 不可能是最短的路径
- 无向:两个节点彼此指向对方,其实就是环
- 无向图:每条边其实就是一个环。
- 有向无环图:directed acyclic graph,DAG,狄克斯特拉算法仅适用于此
应用:换钢琴
- 不同的同学手上有一些item
- 物品彼此之间可交换,可能需要添加费用
-
从某个同学出发,如何最少的费用换取其他心仪的物品?
- 准备:
- 构建图
- 创建节点开销表格,用于存储到每个节点的最小距离,会不断更新
-
创建父节点表格,用于最后追溯出具体的最短路径
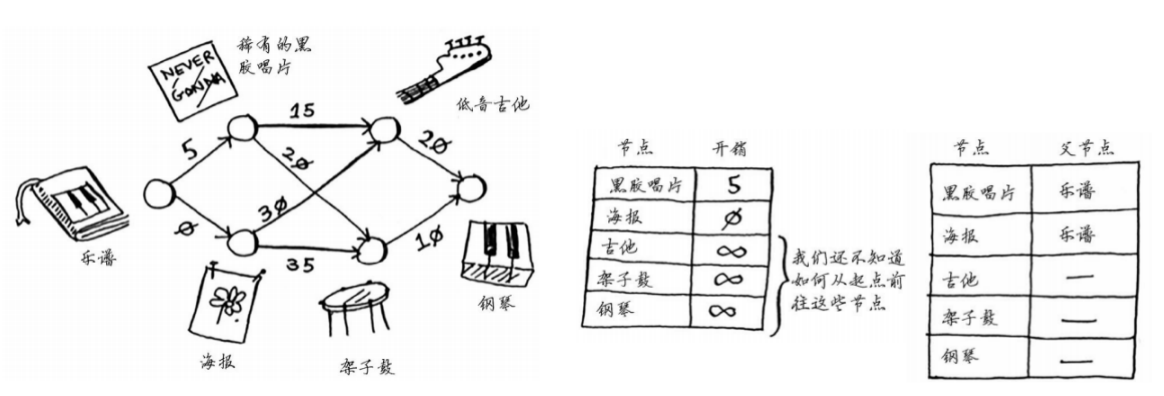
-
一次寻找最便宜节点,更新其邻居节点
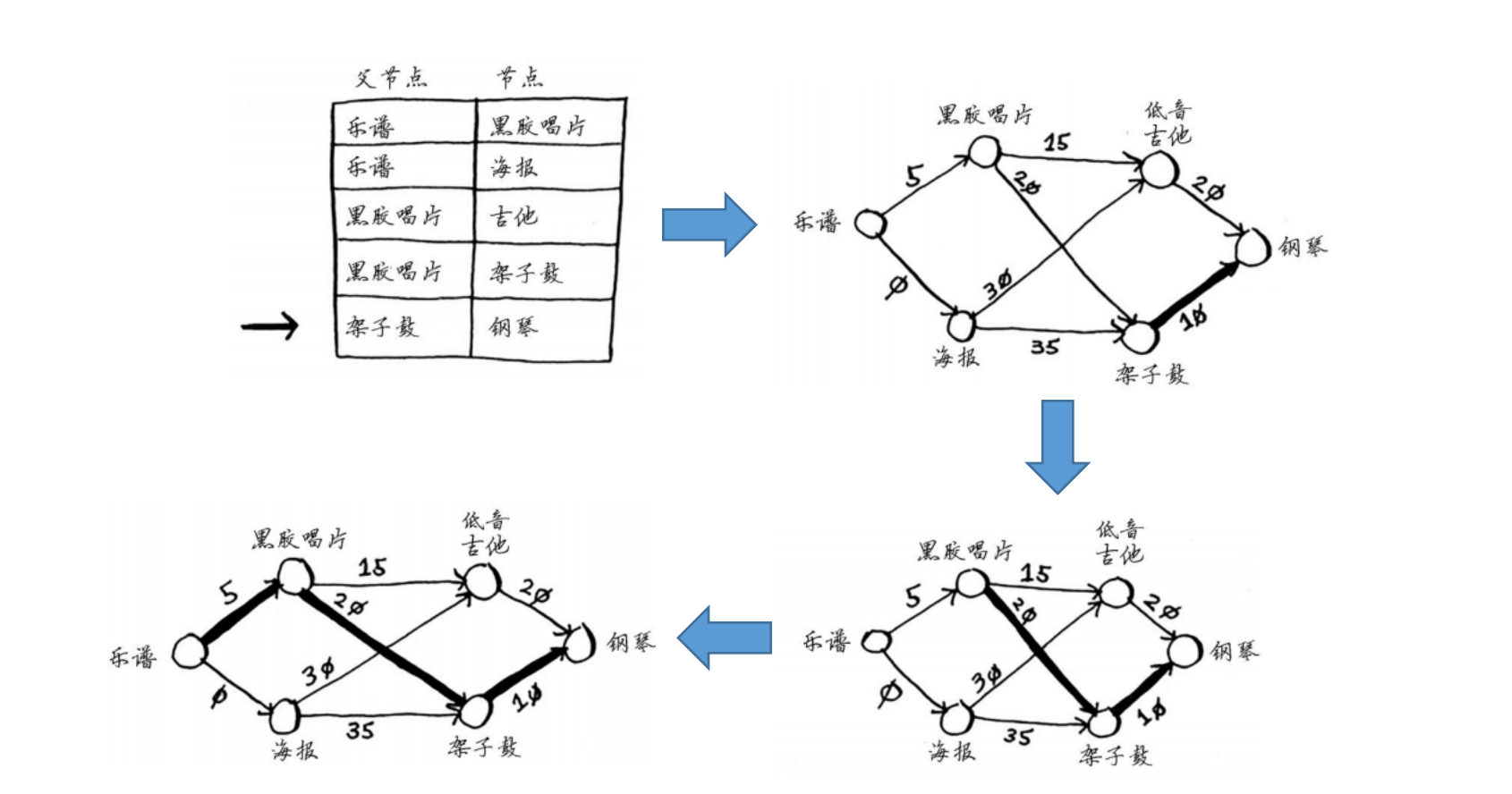
- 根据父节点表格回溯出最短路径
负权重
- 下面是个例子:
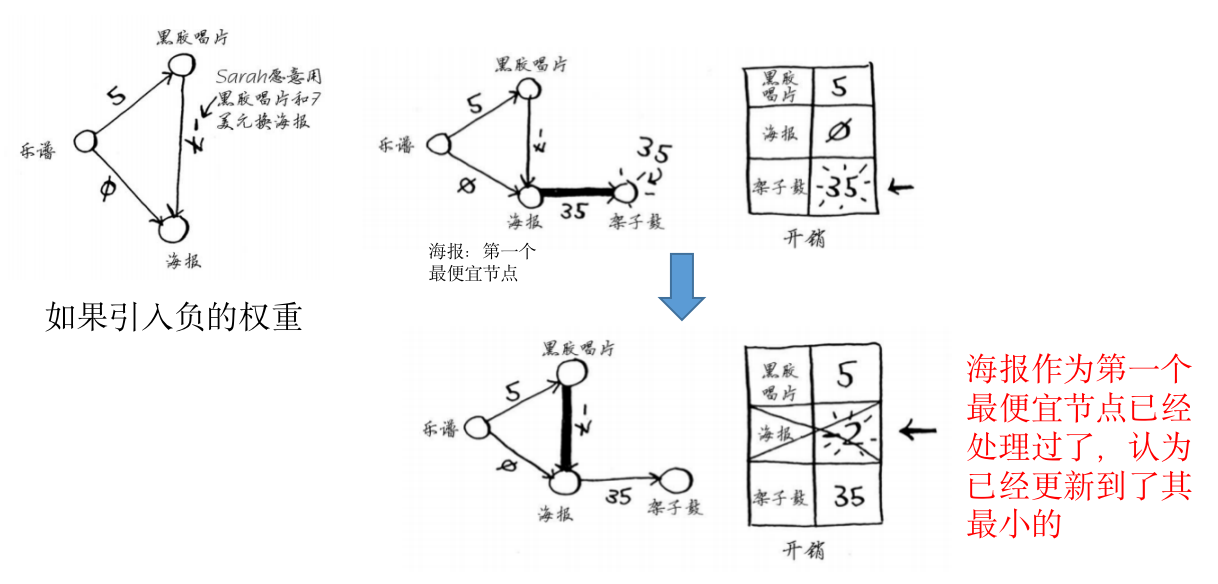
- 狄克斯特拉算法:
- 假设:对于处理过的节点(之前的最便宜的节点),没有前往该节点的更短路径
- 假设成立条件:在没有负权重时才成立
- 另一种算法:贝尔曼-福德算法,Bellman-Ford algorithm
实现
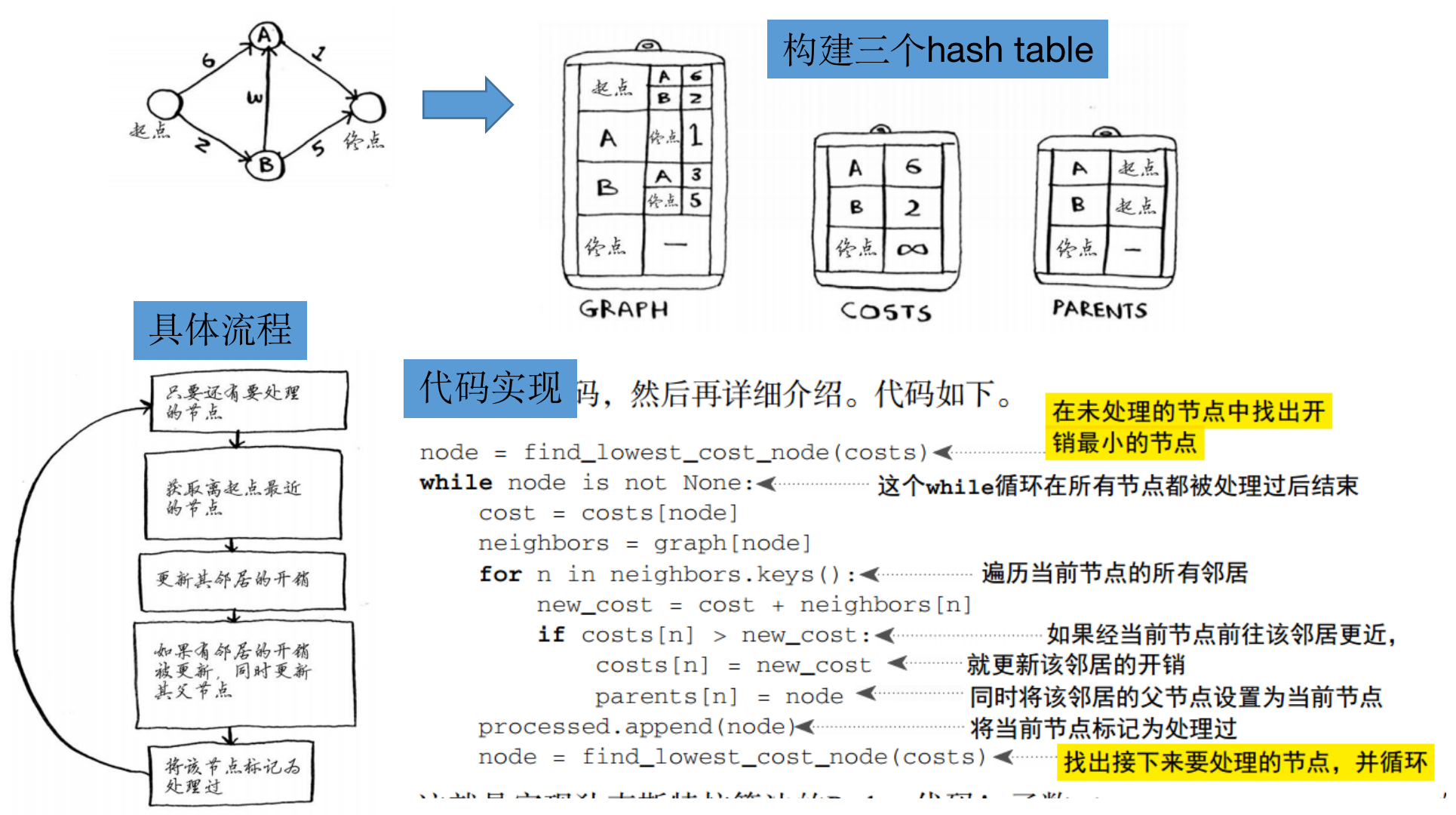
# the graph
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {}
# the costs table
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity
# the parents table
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
processed = []
def find_lowest_cost_node(costs):
lowest_cost = float("inf")
lowest_cost_node = None
# Go through each node.
for node in costs:
cost = costs[node]
# If it's the lowest cost so far and hasn't been processed yet...
if cost < lowest_cost and node not in processed:
# ... set it as the new lowest-cost node.
lowest_cost = cost
lowest_cost_node = node
return lowest_cost_node
# Find the lowest-cost node that you haven't processed yet.
node = find_lowest_cost_node(costs)
# If you've processed all the nodes, this while loop is done.
while node is not None:
cost = costs[node]
# Go through all the neighbors of this node.
neighbors = graph[node]
for n in neighbors.keys():
new_cost = cost + neighbors[n]
# If it's cheaper to get to this neighbor by going through this node...
if costs[n] > new_cost:
# ... update the cost for this node.
costs[n] = new_cost
# This node becomes the new parent for this neighbor.
parents[n] = node
# Mark the node as processed.
processed.append(node)
# Find the next node to process, and loop.
node = find_lowest_cost_node(costs)
print("Cost from the start to each node:")
print(costs)
参考
Read full-text »
Algorithm: 图及图搜索
2017-01-22
目录
图
- 路程问题:
- 从一个地点出发去往另外一个地方,走哪条路最短?
- 步骤:
- 1)使用图模型建立问题模型
- 2)使用广度优先搜索解决问题
- 最短路径问题:
- shortest-path problem
- 找出去往朋友家的最短路径
- 国际象棋中把对方将死的最少步数
- 解决算法:广度优先搜索
- 图:
- 由节点+边组成
- 一个节点可能与众多节点直接相连,这些节点称为邻居
- 模拟一组连接

广度优先搜索
- 回答两类问题:
- (1)从节点A出发,有前往节点B的路径吗?
- (2)从节点A出发,前往节点B的哪条路径最短?
- 例子:在朋友圈找到芒果经销商【第一类问题,有没有】
- 先在自己的朋友里面找,看有没有
- 如果没有的话,把该朋友的朋友也加入到搜索队列的后面,因为后面还要接着搜索
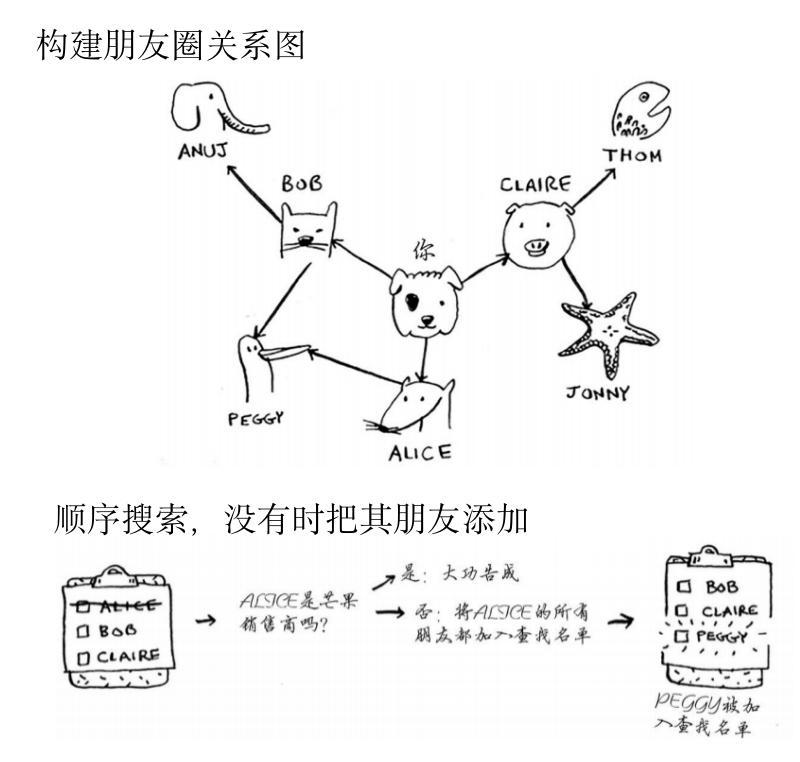
查找最短路径
- 上述的问题中:
- 一度关系胜过二度关系,以此类推
- 先搜索一度关系,再往外延伸
- 因此一度关系在二度关系之前加入查找名单
- 比如顺序添加,先添加先检查
- 数据结构:队列
- queue
- 按添加顺序进行检查
队列
- 原理:与等公交类似,先到先上车
- 操作:
- 不能随机访问队列中元素
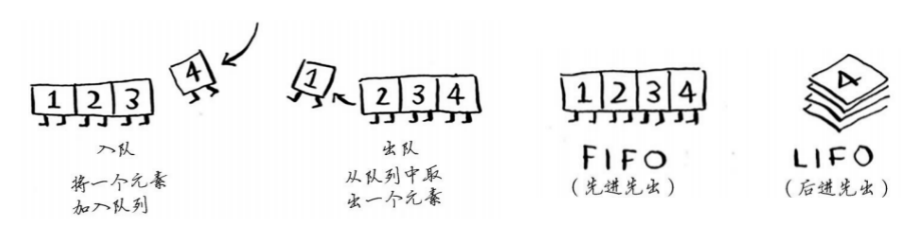
- 入队、出队
- 队列:先进先出,FIFO(first in first out)
- 栈:后进先出,LIFO(last in first out)
图实现
- 有向图:directed graph,关系是单向的
- 无向图:undirected graph,没有箭头,直接互连的节点为邻居
- 散列表实现图:可表示相互之间的归属关系,这个只是存储彼此关系用于查找的,不是搜索的关键,搜索的关键是队列
- 算法实现:
- 创建队列,存储要检查的人
- 弹出一个人,检查是否为经销商
- 是:成功
- 否:将这个人的朋友加入到队列
- 重复弹出检查
- 如果队列为空(全部都检查完),就说明人际关系网中没有经销商

- 注意:
- 搜索的停止条件,1)找到一位经销商,2)队列变为空,即找不到经销商
- 如果某人是两人的朋友,可能需要检查两次
- 标记某人是否检查过,可以使用列表进行记录
- 没有检查过则进行检测
- 否则容易进入死循环。比如你的朋友,其朋友只有你,那么从自己出发,就只会搜索你和他两人。
from collections import deque
# 判断是否为经销商
def person_is_seller(name):
return name[-1] == 'm'
# 构建关系图,存储彼此之间的关系
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []
# 注意这里用的是列表存储朋友
# 即使没有朋友,也需要指定值为空列表
# 因为后面的seach是列表,search列表更新时需要支持直接相加的操作
def search(name):
search_queue = deque()
search_queue += graph[name]
# This array is how you keep track of which people you've searched before.
searched = []
while search_queue:
person = search_queue.popleft()
# Only search this person if you haven't already searched them.
if person not in searched:
if person_is_seller(person):
print(person + " is a mango seller!")
return True
else:
search_queue += graph[person]
# Marks this person as searched
searched.append(person)
return False
search("you")
运行时间
- 沿着边搜索,至少运行O(边数)
- 队列存储检查的人,所以这部分为O(人数)
- 广度优先搜索:O(人数+边数) =》 O(V+E), V:定点数,E:边数
参考
Read full-text »
Algorithm: 散列表(hash)
2017-01-18
目录
散列函数与散列表
- 场景:在杂货店,如果顾客买东西,如何在O(1)的时间查找到对应商品的价格
-
方法1:数组或者链表,每个元素包含商品名称+价格,使用二分查找,时间代价为O(log n)。还是慢,无法满足需求。
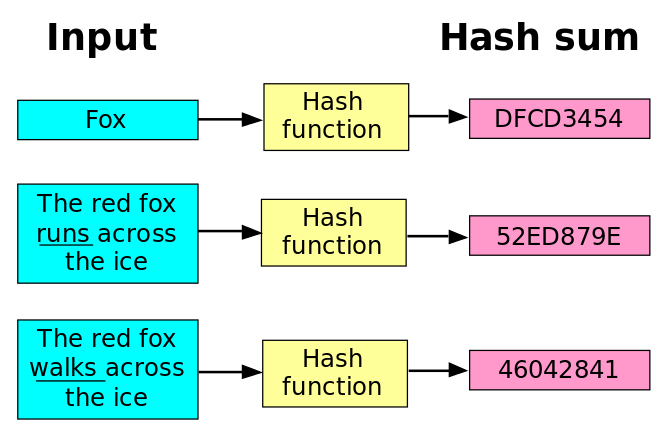
- 散列函数:
- 功能:无论你提供什么数据,都还你一个数字
- 专业描述:将输入映射到数字
- 散列值:通常用一个短的随机字母和数字组成的字符串来代表
- 要求:
- 必须是一致的。什么时候输入一个特定的条目,其输出必须是一样的。
- 将不同的输入映射到不同的数字。如果输出都是一样的,毫无用处。
- 价格存储的例子:
- 输入 =》函数 =》存储的index =》index处的值
- 准确指出价格的存储位置
- 散列表:
- hash table,散列映射、映射、字典、关联数组
- 数组、链表:直接映射到内存
- 散列表:更复杂,使用散列函数来确定元素的存储位置
案例:查找
- 手机电话簿:
- 姓名到电话号码的映射
- 创建映射
- 查找
- 网站:
- 网站名称到IP地址的映射
- 这就是DNS解析(DNS resolution)
案例:防止重复
- 投票:
- 每个人来投票
- 如果未投,则可以投,否则不能再套票。【这其实也是查找的过程】
- 使用散列表来检查是否重复,速度非常快
voted = {}
def check_voter(name):
if voted.get(name):
print("kick them out!")
else:
voted[name] = True
print("let them vote!")
check_voter("tom")
check_voter("mike")
check_voter("mike")
案例:用作缓存
- 访问网页如facebook:
- 1)向facebook服务器发出申请
- 2)服务器做出处理,生成一个网页将其发送给用户
- 3)用户获得一个网页
- 核心:页面的URL映射为页面数据
- 如果某个网页是高度访问的,可以直接存储下来,不用再服务器中间处理的过程,增加访问速度
- 优点:
- 用户更快的看到网页
- facebook需要做的工作更少
冲突
- 理想:将不同的键值映射到不同的地方
- 现实:几乎不可能编写出这样的散列函数
- 冲突:不同的键值被映射到同一个存储位置
- 处理:如果两个键值映射到同一个位置,就在这个位置存储一个链表
- 因此:
- 散列函数很重要
- 如果散列表存储的链表很长,那么查询速度将急剧下降
性能
- 散列表的查找平均是常量时间,简单查找时线性的,二分查找时对数时间的
- 平均情况:
- 查找:与数组一样
- 插入和删除:与链表一样快
- 因此兼具数组和链表的优点
- 最坏情况:
- 查找、插入、删除都是O(n)复杂度
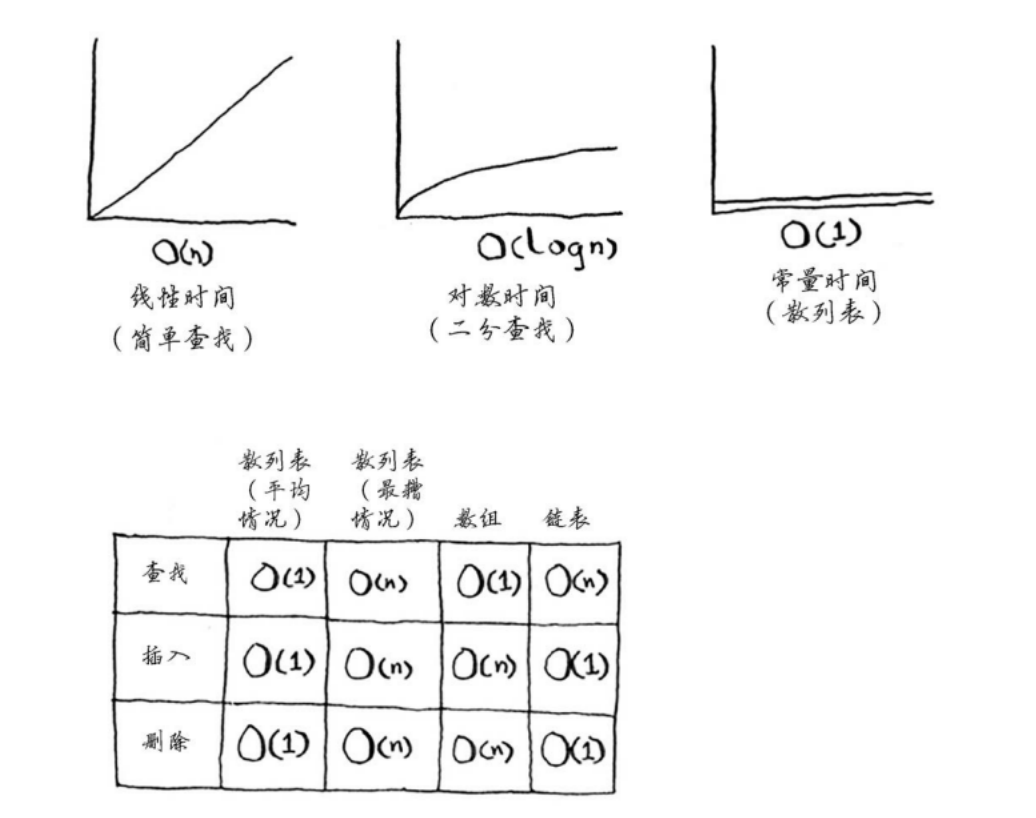
- 查找、插入、删除都是O(n)复杂度
- 如何避免冲突:
- 较低的填装因子
- 良好的散列函数
填装因子
- 填装因子=(散列表包含的元素数目)/(位置总数)
- 散列表是用数组来存储数据,因此需计算数组中被占用的位置数
- 调整长度:当填装因子增大时,需增加散列表的位置
- 经验:一旦填装因子大于0.7,就调整散列表的长度
–
良好的散列函数
- 良好的:散列值呈现均匀分布
- 糟糕的:散列值扎堆,导致大量冲突
参考
Read full-text »
Algorithm: 分治法与快速排序
2017-01-15
分治法
- divide & conquer
- 一种著名的递归式问题解决方法
- 不是一种具体的算法,而是一种思路
- 原理:
- (1)找出简单的基线条件
- (2)确定如何缩小问题的规模,使其符合基线条件
农场问题
- 描述:将一块土地均匀的分成方块,且分出的方块要尽可能大(因为理论上可以分成长度为1的方块)。
- 下面是三种切法:
- 第一个不是方块,不满足
- 第二个都是相同大小的方块,但是数目太多
- 第三个都是方块,但是大小不同,不满足

- 解法策略:
- 可采用分治法的策略
- 第一步:找到基线条件,需尽可能简单。
- 第二步:不断将问题分解,直到符合基线条件。
- 具体实现:
- 基线:如果一个方块的长边L1是短边L2的整数倍,那么这个方块能切分成L1/L2个短边方块,从而无需再继续切分,且此时所用的方块数目也是最少的。

- 切分流程示意:

- 基线:如果一个方块的长边L1是短边L2的整数倍,那么这个方块能切分成L1/L2个短边方块,从而无需再继续切分,且此时所用的方块数目也是最少的。
数组求和
- 描述:给定一个数组,返回数组的和
- 解法1:循环
- 循环数组,不断加和
def sum(arr):
total = 0
for x in arr:
total += x
return total
print(sum([1, 2, 3, 4]))
- 解法2:递归
- (1)找基线条件。
- 当数组为空时,元素和为0
- 当数组仅1个元素时,元素和为第一个元素
- (2)递归调用,缩小数组规模

- (1)找基线条件。
def sum(list):
if list == []:
return 0
return list[0] + sum(list[1:])
- 注意:
- 涉及数组的递归函数,基线条件通常是:数组为空或者只包含一个元素
- 当陷入困境时,请检查基线条件是不是这样的
快速排序
- 常用的排序算法
- 比选择排序快很多
- 采用了分治策略
- 解法:
- (1)基线条件:当数组为空或者只有1个元素时,无需排序,直接返回
- (2)不满足基线条件的,不断缩小规模进行递归调用进行排序
- 实现:
- (1)选择基准值(pivot):从数组中选择1个元素
- (2)分区(partioning):以基准值为阈值,找出比其小和大的值
- 小于基准值的子数组
- 基准值
- 大于基准值的子数组
- (3)排序:对两个子数组进行快速排序
- 例子:

def quicksort(array):
if len(array) < 2:
# base case, arrays with 0 or 1 element are already "sorted"
return array
else:
# recursive case
pivot = array[0]
# sub-array of all the elements less than the pivot
less = [i for i in array[1:] if i <= pivot]
# sub-array of all the elements greater than the pivot
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print(quicksort([10, 5, 2, 3]))
大O表示法
- 常见的大O运行时间对比
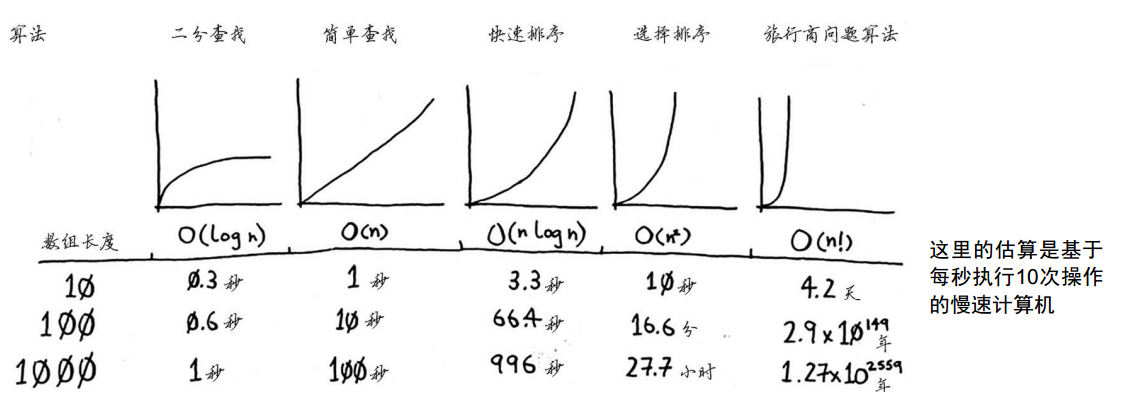
- 算法忽略了固定的时间量:
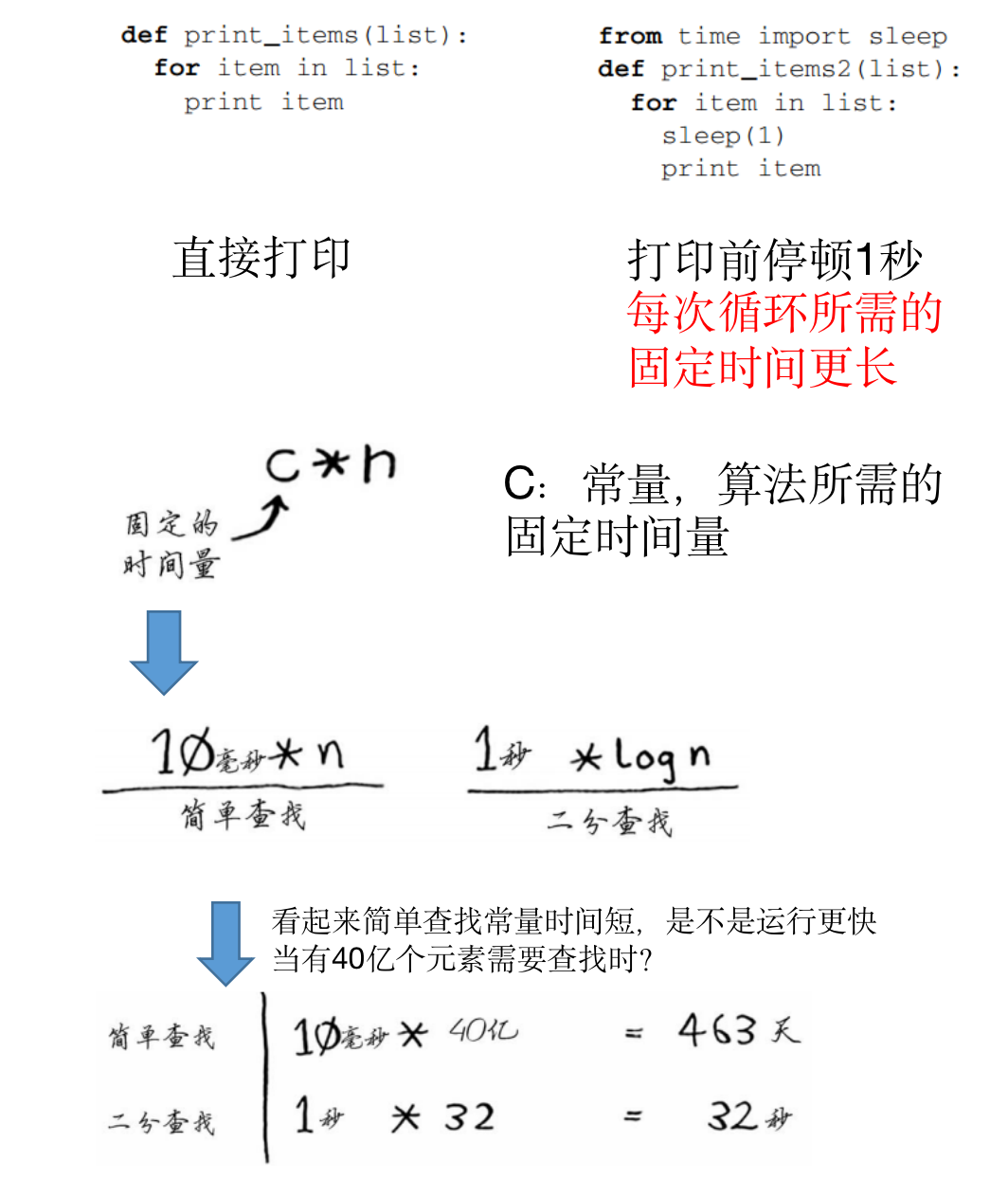
- 注意:
- 快排和合并排序的平均时间都是O(nlog n),但是前者的常量时间更短,所以速度是更快的
- 在简单查找和二分查找,常量几乎无关紧要,因为列表很长
- 平均情况和最糟情况:最佳情况也是平均情况,建议每次随机的选择一个元素作为基准值
- 快速排序:高度依赖于选择的基准值
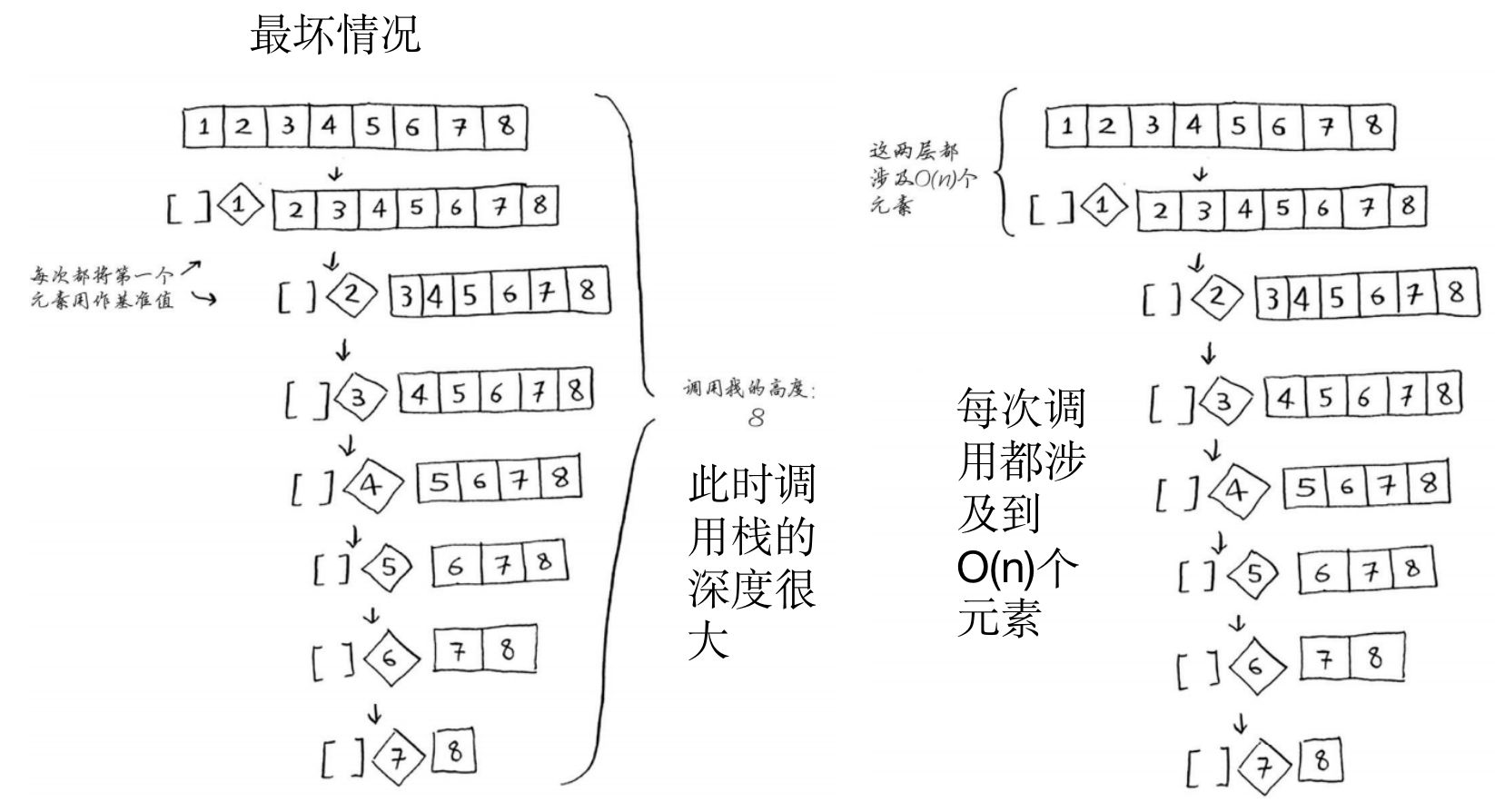
- 例子:对一个有序的数组进行排序
- 最坏情况:此时栈长为O(n)
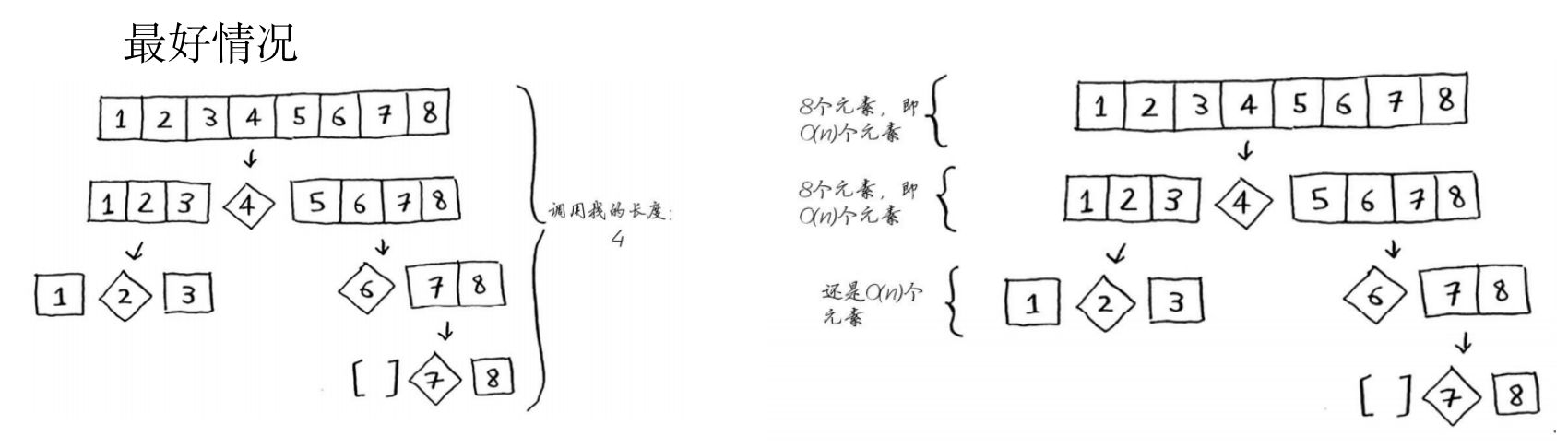
- 最好情况:此时栈长为O(log n)
- 最坏情况:此时栈长为O(n)
参考
Read full-text »
Python module seaborn
2017-01-13
Python seaborn
Read full-text »
Algorithm: 递归与栈
2017-01-12
递归
- 例子:在一堆盒子中找钥匙
- 不同的解决方案:

- while:只要盒子不为空,则每次取出一个检查
- 递归:
- 自己调用自己
- 更清晰,没有性能优势
- 如果使用循环,程序的性能可能更高;如果使用递归,程序可能更容易理解。如何选择要看什么对你来说更重要。
- 此时没有盒子堆,因为栈代替我们这么做了。栈的结构保证我们是否还要检查剩下的盒子堆,以及还有多少需要检查。
- 基线条件
- base case
- 函数不再调用自己,从而避免形成无限循环
- 递归条件
- recursive case
- 函数调用自己
栈

- 例子:创建待办事项清单,即一叠便条
- 操作:压入(插入)和弹出(删除并读取)
- 栈:一种简单的数据结构,可用于存储数据,支持压入和弹出的操作
- 调用栈:计算机在内部使用的栈称为调用栈。用于存储多个函数的变量。
- 所有函数调用都进入调用栈
- 调用栈可能很长,占用大量的内存
- 下面是一个具体的例子,在调用函数的时候,内存的调用情况。可以看到,先调用的入栈,后调用的先被弹出:

递归调用栈
- 递归函数也是使用调用栈
- 例子:阶乘函数
def fact(x):
if x == 1:
return 1
else:
return x * fact(x-1)
- 下面是在此递归调用过程中,内存栈的变化情况:

参考
Read full-text »
Algorithm: 数组、链表、选择排序
2017-01-09
内存的工作原理
- 计算机:很多抽屉的集合体,每个抽屉都有地址
- 内存:每一个带有地址的抽屉,用于存放东西,比如:fe0ffeeb是一个内存单元的地址
- 请求数据存储到地址
- 计算机分配一个存储地址
- 若是多项数据:
- 数组
- 链表
数组

- 例子:待办事项存储
- 数组:在内存中是相连的
- 【缺点:添加元素】很麻烦
- 可预留足够内存:
- 1)多的内存可能用不上,浪费
- 2)当超过内存时,还是得进行数据转移,找到一块更大的内存地址
- 使用链表结构
- 可预留足够内存:
- 【优点:读取元素】:
- 效率很快
- 链表很慢:比如要读取最后一个元素,比如从第一个开始顺序读取,才能获得最后的元素内存地址
链表

- 元素可存储在任何地方
- 每个元素存储了下一个元素的地址,从而使一些列的随机内存地址串在一起
- 类似于寻宝游戏,根据宝物的提示前往下一个地方
- 使用时不需移动元素
- 【优点:添加元素】将新元素放入内存,其地址存到前一个元素中
中间插入、删除
中间插入:
- 链表:修改前面元素的指向地址即可【更好的选择】
- 数组:后面的元素整体向后移动
删除:
- 链表:修改前面元素的指向地址即可【更好的选择】
- 数组:后面的元素整体向前移动
比较:
- 中间插入:如果内存没有足够空间,则会操作失败
- 删除:总能成功
- 时间复杂度:

- 用哪一个?
- 取决于具体情况
- 随机访问:数组的读取方式
- 顺序访问:链表的读取方式
选择排序
- 例子:根据歌曲播放次数进行喜好排序
- 方法:遍历列表,每次找出播放次数最多(最大值)的放在新的列表中

- 时间复杂度:O(n x n)
- 问题:需检查的元素越来越少,为什么是O(n x n)?
- 确实越来越少
- 第一次n个,后面依次是n-1,n-2,。。。,2和1 => 平均:n/2个
- 时间:O(n x n/2)
- 大O表示法:省略常数,比如这里的1/2,因此简写为O(n x n)
python实现
# Finds the smallest value in an array
def findSmallest(arr):
# Stores the smallest value
smallest = arr[0]
# Stores the index of the smallest value
smallest_index = 0
for i in range(1, len(arr)):
if arr[i] < smallest:
smallest_index = i
smallest = arr[i]
return smallest_index
# Sort array
def selectionSort(arr):
newArr = []
for i in range(len(arr)):
# Finds the smallest element in the array and adds it to the new array
smallest = findSmallest(arr)
newArr.append(arr.pop(smallest))
return newArr
print(selectionSort([5, 3, 6, 2, 10]))
参考
Read full-text »
旅行商问题
2017-01-08
问题背景
描述:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
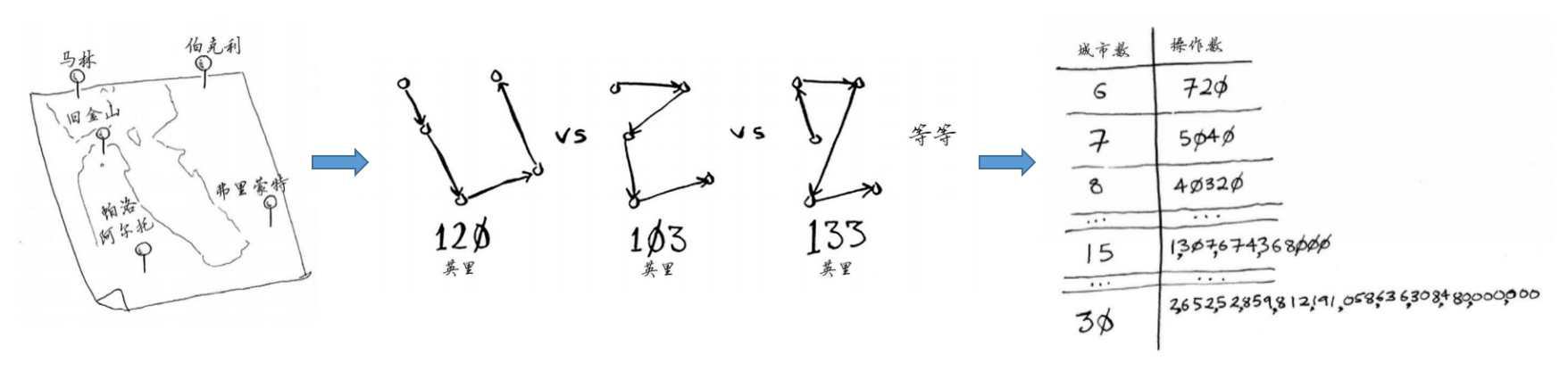
- travelling salesman problem, TSP,又称为最短路径问题
- 组合优化中的一个NP困难问题:再最坏的情况下,随着城市数量的增加,时间复杂度(n!)是指数级别的增长
借助itertools暴力破解
import itertools
# 输入一般是各城市之间的距离
dis = [
[0.00, 24.04, 68.37, 37.66, 58.81, 75.77, 65.20, 57.44, 59.37, 18.61],
[24.04, 0.00, 89.58, 57.41, 82.04, 95.54, 59.86, 78.53, 73.57, 16.23],
[68.37, 89.58, 0.00, 69.97, 18.91, 11.62, 86.73, 11.05, 34.42, 75.40],
[37.66, 57.41, 69.97, 0.00, 52.75, 80.83, 101.03, 61.86, 78.96, 56.26],
[58.81, 82.04, 18.91, 52.75, 0.00, 30.52, 92.05, 16.56, 45.24, 69.97],
[75.77, 95.54, 11.62, 80.83, 30.52, 0.00, 85.08, 19.42, 31.47, 80.50],
[65.20, 59.86, 86.73, 101.03, 92.05, 85.08, 0.00, 78.57, 53.61, 48.83],
[57.44, 78.53, 11.05, 61.86, 16.56, 19.42, 78.57, 0.00, 28.99, 64.41],
[59.37, 73.57, 34.42, 78.96, 45.24, 31.47, 53.61, 28.99, 0.00, 57.41],
[18.61, 16.23, 75.40, 56.26, 69.97, 80.50, 48.83, 64.41, 57.41, 0.00],
]
def getDis(path):
d = sum([dis[path[i]][path[i + 1]] for i in range(len(path) - 1)] + [dis[path[-1]][path[0]]])
# print(path, path[-1], path[0], d)
return d
min_dis = 111111111111
min_path = []
for path in itertools.permutations(range(len(dis))):
# print(i)
if min_dis >= getDis(path):
min_dis = getDis(path)
min_path.append(path)
for p in min_path:
print(p)
print(min_dis)
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
(0, 1, 2, 3, 4, 5, 6, 8, 7, 9)
(0, 1, 2, 3, 4, 5, 7, 6, 8, 9)
(0, 1, 2, 3, 4, 5, 7, 8, 6, 9)
(0, 1, 2, 3, 4, 7, 5, 8, 6, 9)
(0, 1, 2, 4, 3, 7, 5, 8, 6, 9)
(0, 1, 2, 4, 5, 7, 8, 6, 9, 3)
(0, 1, 2, 4, 7, 5, 8, 6, 9, 3)
(0, 1, 3, 2, 4, 5, 7, 8, 6, 9)
(0, 1, 3, 2, 4, 7, 5, 8, 6, 9)
(0, 1, 3, 4, 2, 5, 7, 8, 6, 9)
(0, 1, 3, 4, 7, 2, 5, 8, 6, 9)
(0, 1, 9, 6, 8, 2, 5, 7, 4, 3)
(0, 1, 9, 6, 8, 5, 2, 7, 4, 3)
(2, 5, 8, 6, 9, 1, 0, 3, 4, 7)
(3, 4, 7, 2, 5, 8, 6, 9, 1, 0)
(4, 7, 2, 5, 8, 6, 9, 1, 0, 3)
(5, 2, 7, 4, 3, 0, 1, 9, 6, 8)
303.81999999999994
参考
Read full-text »
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me

