tSNE分析
2018-12-09
概述
T 分布随机近邻嵌入(t-distributed Stochastic Neighbor Embedding):对高维的数据进行降维可视化,识别相关联的模式,保持局部结构(高维空间中距离相近的点投影到低维中扔然相近)。
原理
- 对数据点近邻分布进行建模。高维空间:高斯分布 =》低维空间(比如二维空间):t分布(更长的尾部,更均匀分布)。
- 下图红色为t分布,蓝色为正太分布:

- 目标:找到一个变换,将高维空间投射到二维空间,最小化所有点在这两个分布之间的差距。
- 困惑度(Perplexity):拟合分布时考虑的近邻数。低困惑度:最近的几个近邻。
- 分布时基于距离的,需要所有数据为数值型。类别变量:二值编码等进行转换。
- 随机近邻嵌入:
- 数据点的欧几里德距离转换为条件概率而表征相似性。如果两个点相近,则一个呗选为另一个的近邻的条件概率高。

- 引入矩阵(低维空间的)Y,同样计算条件概率:
.png)
- 整体目标是对于Y中的点,使其条件概率分布近似于原始高维空间,所以可以构建损失函数如下,并用梯度下降寻找最小值。
.png)
实现
因为tSNE在生物学的单细胞分析里比较多,所以利用已发表的数据重现一下文章的图。
- 文章:Jindal et al. Discovery of rare cells from voluminous single cell expression data. Nature Communications. 2018
- 数据:preprocessedData_jurkat_two_species_1580.txt.gz
sklearn版本
导入模块:
import seaborn as sns
import pandas as pd
import sklearn.manifold as skma
import gzip
import numpy as np
读取数据:
with gzip.GzipFile('./preprocessedData_jurkat_two_species_1580.txt.gz', 'r') as fid:
preprocessedData = np.genfromtxt(fid)
print type(preprocessedData)
print preprocessedData.shape
# <type 'numpy.ndarray'>
# (1580, 1000)
做tSNE并保存结果:
tsne = skma.TSNE()
projs = tsne.fit_transform(preprocessedData)
np.savetxt('preprocessedData_jurkat_two_species_1580.tsne.txt', projs)
可视化的结果:
f = './preprocessedData_jurkat_two_species_1580.tsne.txt'
df1 = pd.read_csv(f, header=None, sep=' ')
df1.columns = ['tSNE-1', 'tSNE-2']
df1.head()
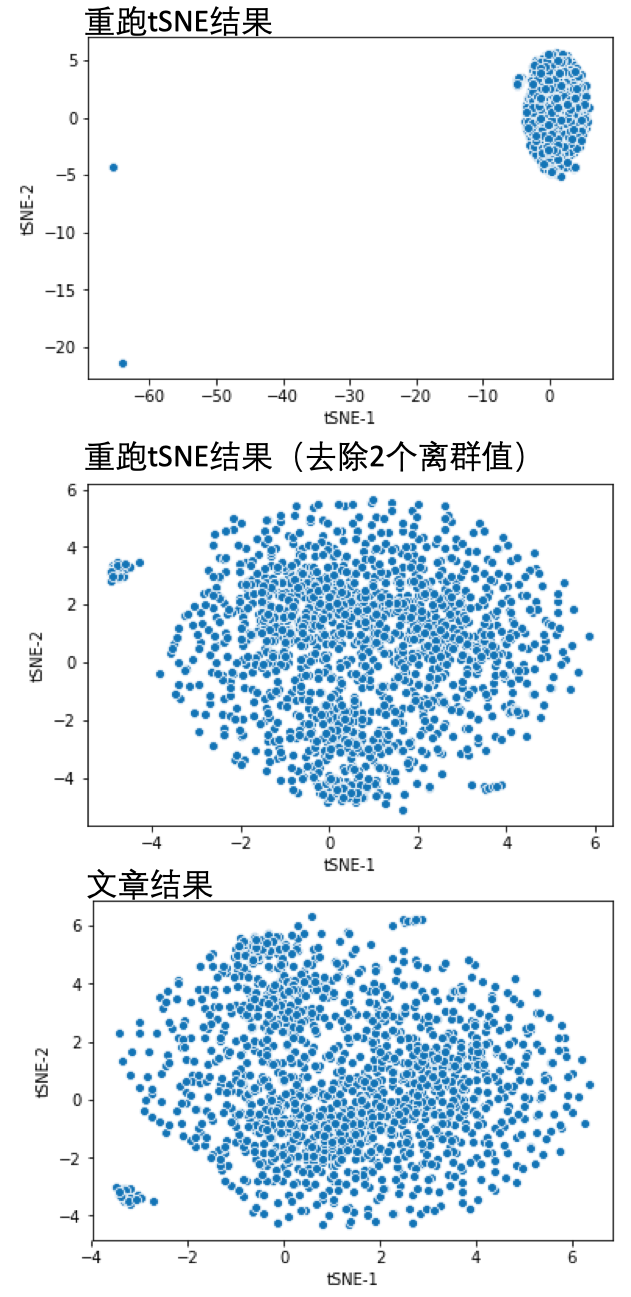
sns.scatterplot(x='tSNE-1', y='tSNE-2', data=df1)
可以看到有两个离群值,将其去除后在可视化:
df1_filterOutliner = df1[df1['tSNE-1']>-20]
sns.scatterplot(x='tSNE-1', y='tSNE-2', data=df1_filterOutliner)
文章提供的结果:
f = './tsne_jurkat_1k_outlierRemoved.txt'
df2 = pd.read_csv(f, header=None, sep=' ')
df2.columns = ['tSNE-1', 'tSNE-2']
df2.head()
sns.scatterplot(x='tSNE-1', y='tSNE-2', data=df2)
可以看到,两个图不完全一样,因为tSNE函数会设置初始状态值,不同的值结果存在偏差,可以结合聚类的结果看是不是大致相似。
参考
Read full-text »
ICA独立成分分析
2018-12-07
概述
独立成分分析(Independent Component Analysis, ICA):类似于PCA,找到一组新的基向量(basis)来表征样本数据,但是PCA用于服从高斯分布的数据,ICA用于服从非高斯分布的数据。
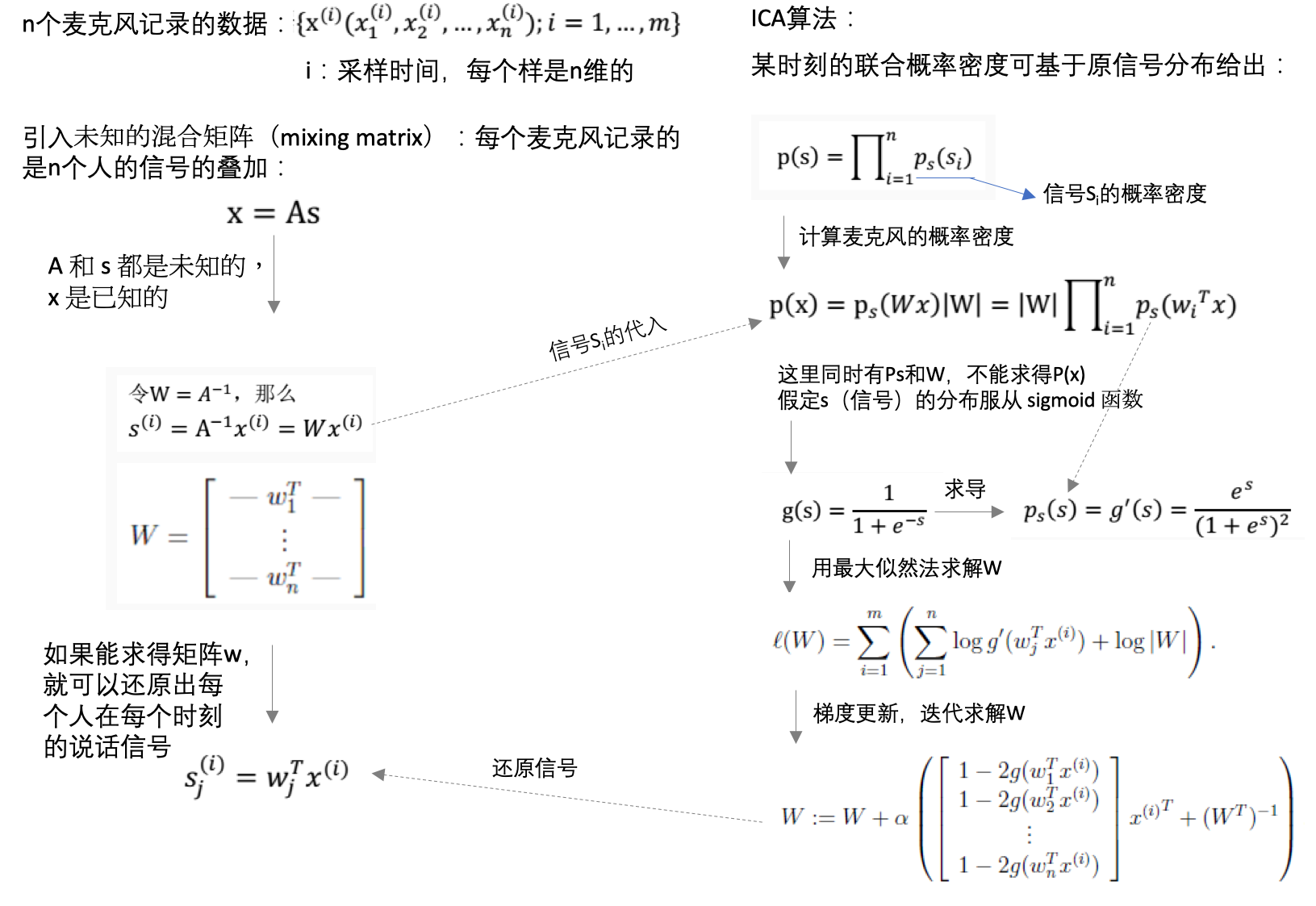
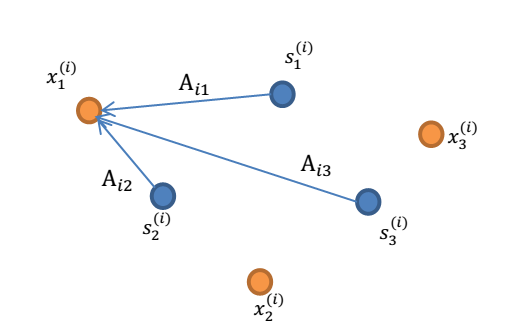
经典案例就是“鸡尾酒宴会问题”:
在一个聚会场合中,有\(n\)个人同时说话,而屋子里的任意一个话筒录制到底都只是叠加在一起的这\(n\)个人的声音。但如果假设我们也有 \(n\)个不同的话筒安装在屋子里,并且这些话筒与每个说话人的距离都各自不同,那么录下来的也就是不同的组合形式的所有人的声音叠加。使用这样布置的\(n\)个话筒来录音,能不能区分开原始的\(n\)个说话者每个人的声音信号呢?
知识点
1、适用场景:
- 数据不服从高斯分布
- 数据信号是相互独立的
3、ICA vs PCA:
参考
- 机器学习15-3—独立成分分析ICA(Independent Component Analysis)
- 独立成分分析(Independent Component Analysis)
- CS229 课程讲义中文翻译: 第十二部分 独立成分分析
- ICA @UFLDL Tutorial
Read full-text »
[CS229] 14: Dimensionality Reduction
2018-12-05
14: Dimensionality Reduction
- 降维:非监督学习算法,用更简化的表示方法表征收集的数据。
- 为啥降维 -》压缩:
- 为啥降维 -》可视化:
- 高维数据难以可视化
- 降维可以将数据以人可以理解的方式展现出来
- 比如一个表格,使用了50多个特征描述不同的国家,从这里我们能得到什么信息?
- 通常很难理解具体的降维之后的特征所表示的意思
- 主成分分析(PCA):
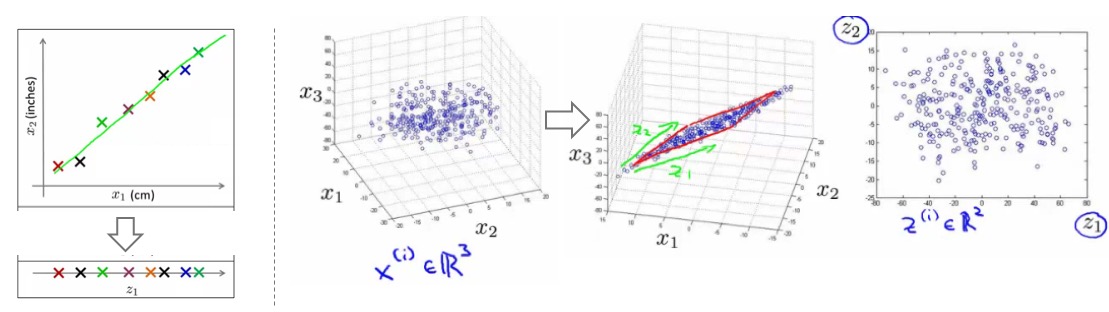
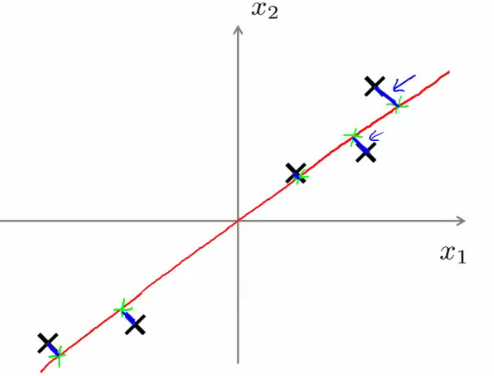
- 例子:2D数据降至1D,所以需要找一个一维的向量,使得所有点在这个向量的投射误差最小:
- 投映误差(projection error):点到向量的垂直距离(orthogonal distance),下图中的蓝色线条
- 在做PCA之前,一定要对数据进行预处理:平均值归一化(mean normalization)和特征缩放(feature scaling)
- 广泛定义:
- nD -> kD,在将数据从
n维降至k维时,需要找k个向量,使得所有数据投射到这些向量时,投映误差最小。找的向量需要能最大程度的保留原来的信息,冗余的信息可以只保留部分信息,所以需要找的向量应该是波动最大(variance最大)的方向,这样也能保证投射误差最小。所以选取的k个方向,也是差异最大的k个方向。3D -> 2D:找两个向量。 - 特征向量:数据变化的方向向量。一个k维的数据,就有k个变化的方向,且不同的方向变化大小是不一样的。
- PCA vs 线性回归:
- PCA和线性回归很像,但PCA不是线性回归,其差别很大
- 线性回归:拟合直线,使得y方向的差值(vertical distance,预测的误差)最小,因为线性回归是有y值的;
- PCA:没有y值,只有特征值(且这些特征值都是同等对待的)。所以是找向量,误差的计算用的是垂直距离(orthogonal distance)。
- PCA算法:
- 【预处理:均值归一化】:对于每个特征,进行均值归一化,x -> x-mean(x)。每个特征的均值归一化到0.
- 【预处理:特征缩放】:当特征的区间差异很大时,需要进行缩放使得数值在可比较的区间里。1)Biggest - smallest;2)Standard deviation(标准差缩放更常见)
- 计算2个向量:1)新的平面向量u;2)新的特征向量z。
- 比如2D -> 1D,要计算向量u和新的特征向量:
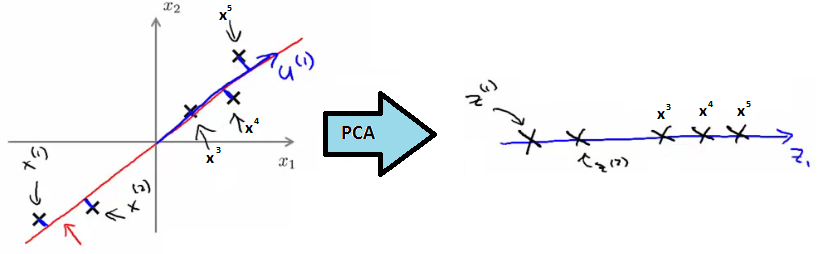
- 算法描述(这里有计算的步骤描述,可参考):
- 1)数据预处理:中心化,归一化。(对于图像、音频、文本等数据,通常不用做variance normalization归一化,比如特征乘以一个数,PCA计算的特征向量是一样的。)
- 2)根据样本计算协方差矩阵
- 3)利用特征值/奇异值分解,求特征值和特征向量
- 4)用特征向量构造投影矩阵
- 5)利用投影矩阵和样本数据,计算降维的数据
- 如何选取k:
- 通常会定义一个比值=平均投影误差/数据本身总方差:
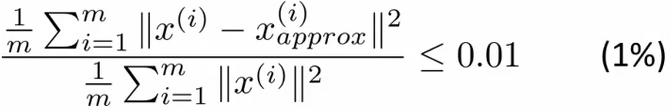
- 这个数值越小越好,越小说明丢失的信息越少,保留的信息越多。
- 实际操作:从k=1开始尝试,看哪个能满足上面的比值<=0.01,最小的能够满足这个比例的k值是我们想要的:

- 通过投影矩阵还原原始数据,我们只能用一个近似的原则。因为保留的k维是原始数据差异最大的,其他的维度差异近似为0,所以可以通过补充0的方式,来(近似)还原原始的数据:\(\begin{align} \hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}\)
- 通常会定义一个比值=平均投影误差/数据本身总方差:
- PCA可加速监督式学习算法:
- 比如对于具有超高维特征的数据,可先用PCA进行降维,使用降维后的数据和原始的标签进行模型的训练,再去对于新的数据进行预测。
- 新数据:怎么预测?特征数目或者叫维度不一样!!!在上面的PCA中计算了参数投影矩阵。
- PCA应用:
- 压缩:减少存储,加速算法。保留多少的variance来确定k值。
- 可视化:通常降至2-3维
- 错误使用PCA避免过拟合:以为具有更少的特征就能避免过拟合,实则不然。应该使用正则化防止过拟合。
- 至少95%-99%的信息是需要保留的。
- 在使用PCA之前,先尝试不使用时能否达到预期的效果。
- 白化(whitening):目的是降低特征之间的相关性,特征的方差归一化
- 训练图片,相邻的像素是高度冗余的(特征具有强相关性)
- 通常学习算法希望的特征是:1)不相关的;2)具有相同的variance(彼此方差接近)。
- PCA-whitening:
- 是基于PCA的,包括两个步骤
- 1)使用PCA进行降维,消除特征之间的相关性:\(\textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}\)
- 2)方差归一化:\(\begin{align} x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \end{align}\)
- 这样就得到了白化的PCA,依然选取前k个作为主成分。
- ZCA-Whitening:
- 另外的一种白化方式,同样能够实现减少相关特征,方差归一化的目的。
- UFLDL笔记 - PCA and Whitening 一文较为详细的描述了PCA白化和ZCA变化的区别,可以参考一下。
- PCA白化是将原始数据投影到主成分轴上(消除特征相关性),然后对特征轴上的数据进行归一化(方差全缩放为1)。这些操作是在主成分空间完成的,为了使得白化的数据尽可能接近原始数据,所以可以把白化的数据转换回原始数据,这就是ZCA白化所做的事情。
- ZCA白化相当于将经过PCA白化后的数据重新变换回原来的空间。
Read full-text »
深度学习
2018-12-02
目录
神经网络 neural network
- 构成:一层一层神经元
- 作用:帮助提取原始数据中的模式(特征),pattern feature extraction
- 关键:计算出每个神经元的权重
- 方法:使用BP算法,利用梯度递减或者随机梯度递减,得到每个权重的最优解
神经网络划分和比较
划分依据:
- 层数
- 神经元个数
- 模型复杂度
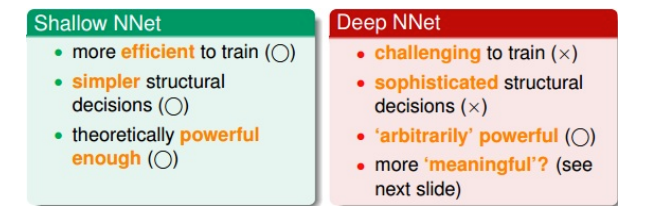
深浅神经网络比较:
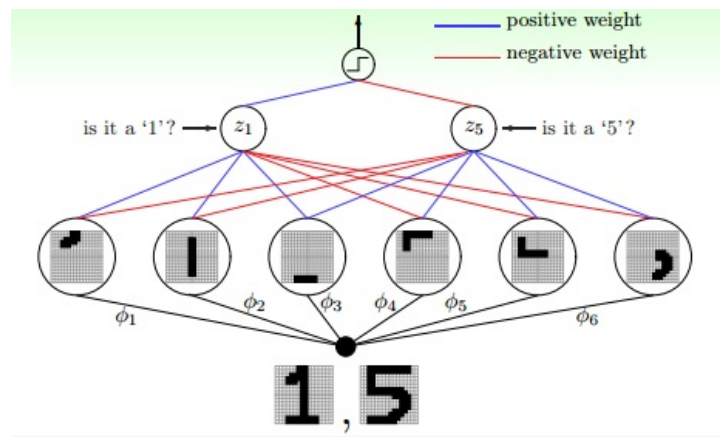
神经神经网络例子:数字识别
- 在电脑视觉和语音识别领域应用广泛
- 一层一层的神经网络有助于提取一些物理特征
- 比如识别手写数字:
深度学习的挑战与应对
- 难以确定应该使用什么样的网络结构:层次太深,可能性太多
- 模型复杂度很高
- 难以优化
-
极大的计算量
- 关键:
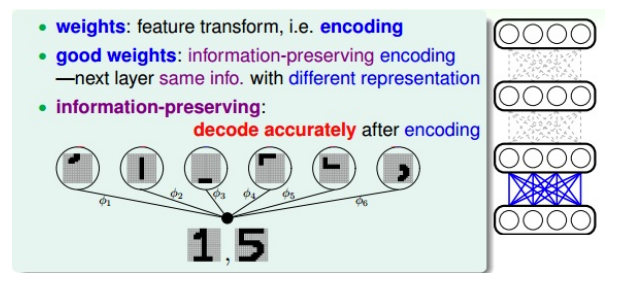
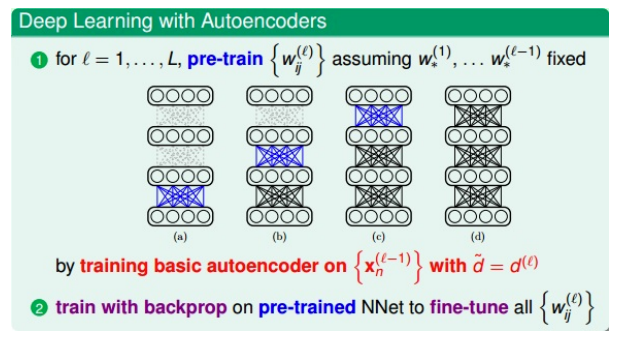
pre-training:autoencoder
好的权重:最大限度保留特征信息
- 一种特征转换
- 也是一种编码,把数据编码成另外一些数据来表示
- 好的权重初始值?
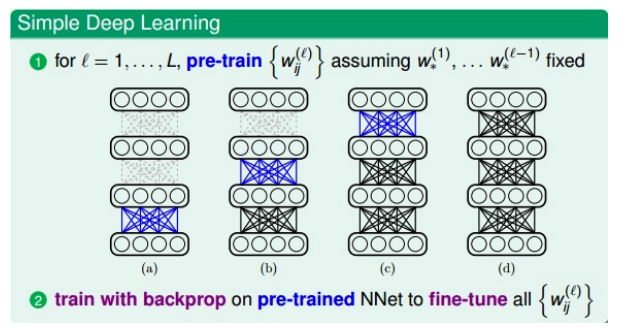
pre-train:如何得到好的初始权重
- 方法:
- 用途:
- 核心:
- 训练过程:
- 对第一层(输入层)进行编码和解码,得到权重\(W_{ij}^{(1)}\)$,作为网络第一层到第二层的初始化权重
- 对网络第二层进行编码和解码,得到权重\(W_{ij}^{(2)}\)$,作为网络第二层到第三层的初始化权重
- 以此类推
- 注意1:每次的目的是得到深度神经网络(自己定义的)中某两层之间(比如
l-1层到l层)的初始化权重,而这个权重是通过上面的简单的三层autoencoder网络训练的到的 - 注意2:对于深度神经网络中的
l-1层的网络,autoencoder中的隐藏层应该与深度神经网络中的下一层l层的神经元个数相同,这样才能得到相同数目的权重
控制复杂度:正则化
- 神经元和权重个数非常多
- 模型复杂度很大
- 需要正则化
- 常用的正则化方法:
- structural decisions/constrains
- weight decay or weight elimination regularizers
- early stopping
- denoising:在深度学习和antoencoder中效果很好
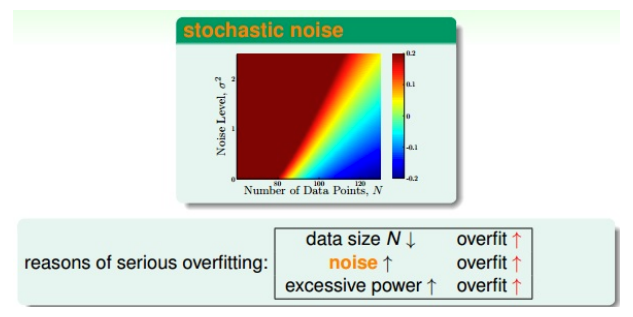
哪些原因导致模型的过拟合?
如何去除噪声?
- 对数据进行清洗:直接操作,麻烦、费时费力
-
在数据中添加一些噪声:疯狂的操作
- 添加噪声的想法
- 来源:如何构建一个健壮的autoencoder
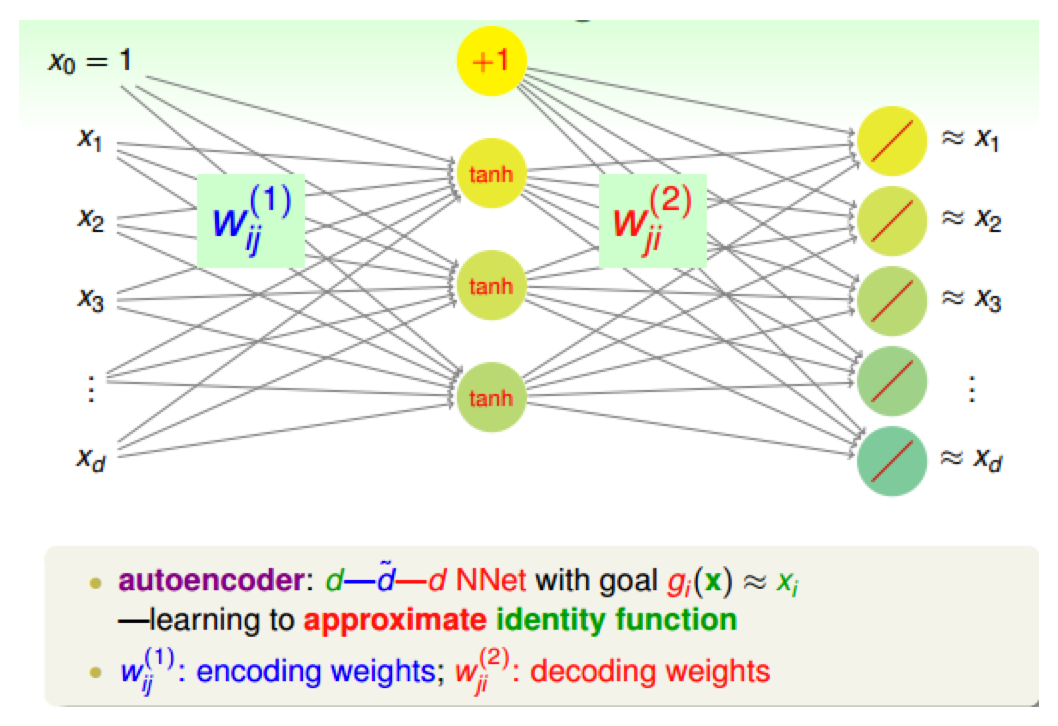
- autoencoder:编码解码后的g(x)会非常接近真实值x
- 如果对输入加入噪声,健壮的autoencoder,应该是使得输出g(x)同样接近真实值x
- 例子:识别数字,如果数字是歪斜的,经过编码解码后也能正确识别出来
- 所以这种autoencoder是很健壮的,起到了抗噪声和正则化的作用
denoising autoencoder
- 编码+解码
- 去噪声、抗干扰:输入一些混入了噪声的数据,仍然能够得到纯净的数据
- 加入噪声的数据集:\({(\check{x}_1, y_1=x_1),...,(\check{x}_N, y_N=x_N)}, \check{x}_n=x_n+noise\),\(x_n\)是纯净样本
- 训练目的:让\(\check{x}_n\)经过编码解码之后能恢复为纯净的\(x_n\)

linear autoencoder
- denoising autoencoder:非线性的,激活函数是tanh
- linear autoencoder:比较简单,PCA很类似
- 两者的计算:
- PCA会对原始数据进行减去平均值的操作
- 都可用于数据压缩或者降维,但是PCA更加广泛

参考
Read full-text »
[CS229] 13: Clustering
2018-11-29
13: Clustering
- 聚类:从无标签的数据中学习,是非监督的学习。
- 监督式:有标签,用模型去拟合
- 非监督式:尝试鉴定数据的结构,基于数据的结构把数据聚集起来
- 场景:1)市场分割(顾客分类);2)社交网络分析;3)集群构架;4)天文数据分析(理解银河系信息)
- sklearn提供了一个常见聚类算法的比较:
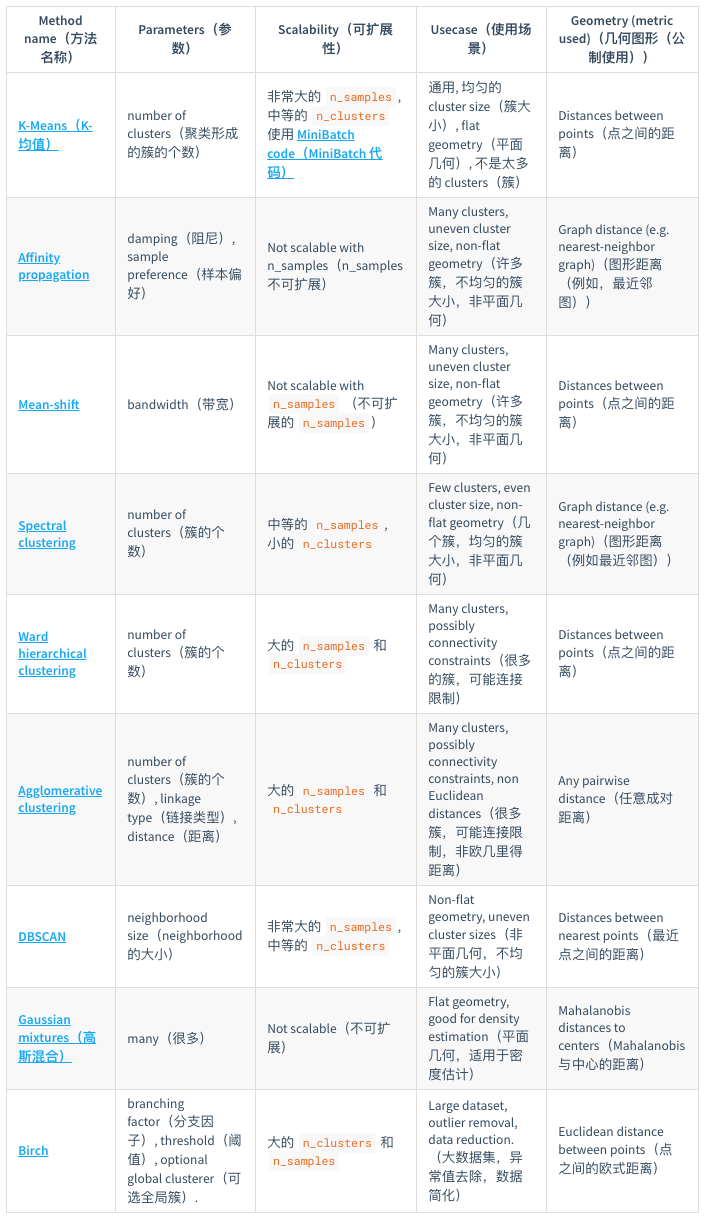
- k-means算法(至今最广泛使用的聚类算法):
- 【1】随机初始化类中心(比如K个)
- 【2】类分配(cluster assigned step)。对数据集中的每个样本,分配其属于最近的类中心的那个类。
- 【3】中心移动(move centroid step)。每个类的点的中心重新计算。
- 正式的定义:
- 比如K个类别,x1,x2,。。。,xn个样本,算法的步骤如下:

- 有的中心没有数据:
- 去除掉这个中心,最后得到K-1个类
- 重新对K个中心初始化选取(不一定100%work)
- 不易分隔的类别:
- 实际应用中,有的数据集或者问题没有明显的类别界限,亦可尝试k-means
- 例子:根据身高和体重信息,做不同大小的衣服
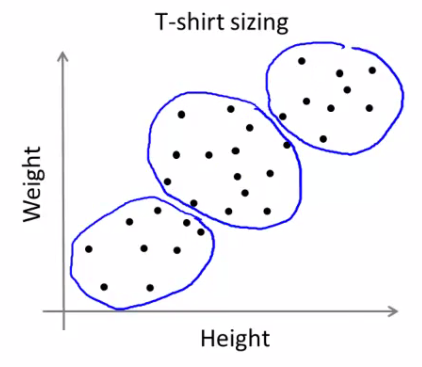
- 损失函数:
- 和监督式学习一样,非监督式学习也有优化的目标或者损失函数
- 损失函数如下(最小化每个数据点与其所关联的聚类中心点之间的距离之和):
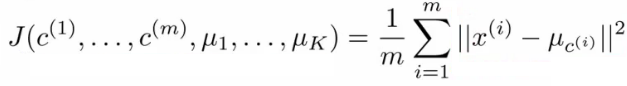
- 类分配步骤就是寻找合适的c1,c2,。。。,cm,使得损失函数最小
- 中心移动步骤就是寻找合适的μ,使得损失函数最小。
- 关于如何理解损失函数优化,可以参考这篇文章
- 随机初始化:
- 如何初始化以避免局部最优?
- 常见做法:随机从训练样本中选取K个作为初始的中心。
- 不同的初始化会得到不同的聚类结构,有可能陷入局部最优,比如下图:
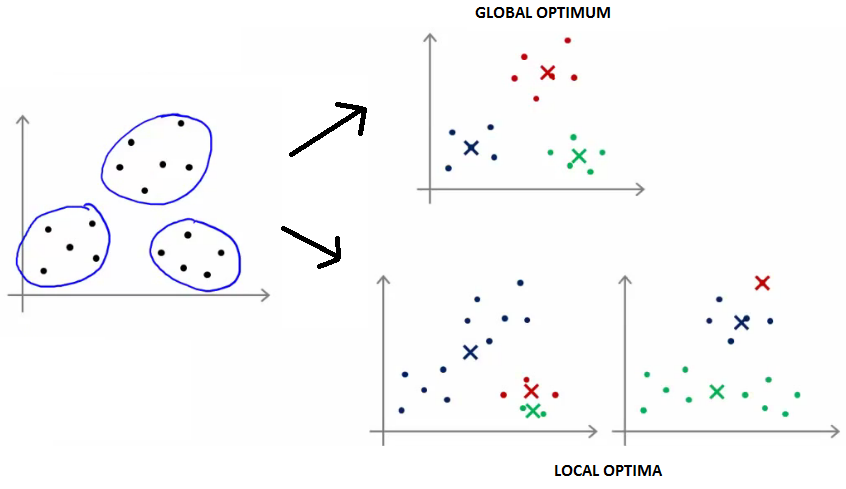
- 如何解决局部最优:可以多做几次(通常50-1000次)随机初始化,看结果是否都是这样的。更具体的是,随机初始化50-1000次,每次计算对应的损失值,取最小的损失值的。
- 当类别K在2-10时,多次随机初始化比较有效果
- 当类别K大于10时,多次随机初始化没有特别必要
- 如何选取类别数K:
- 没有好的自动化的方式进行设定,通常可以可视化数据集协助判断
- Elbow方法:选取一系列的K,画关于K的损失值分布,选取损失值最小所对应的K。
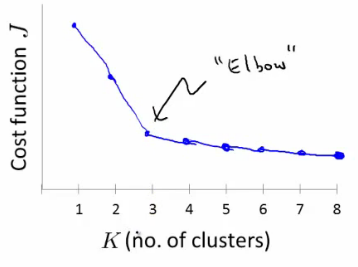
- 根据后续的结果反馈来判断,可以先做几个不同数目K的结果,根据此类别数据的用途来判断这种大小的K值是否合适。
Read full-text »
[CS229] 12: Support Vector Machines
2018-11-25
12: Support Vector Machines
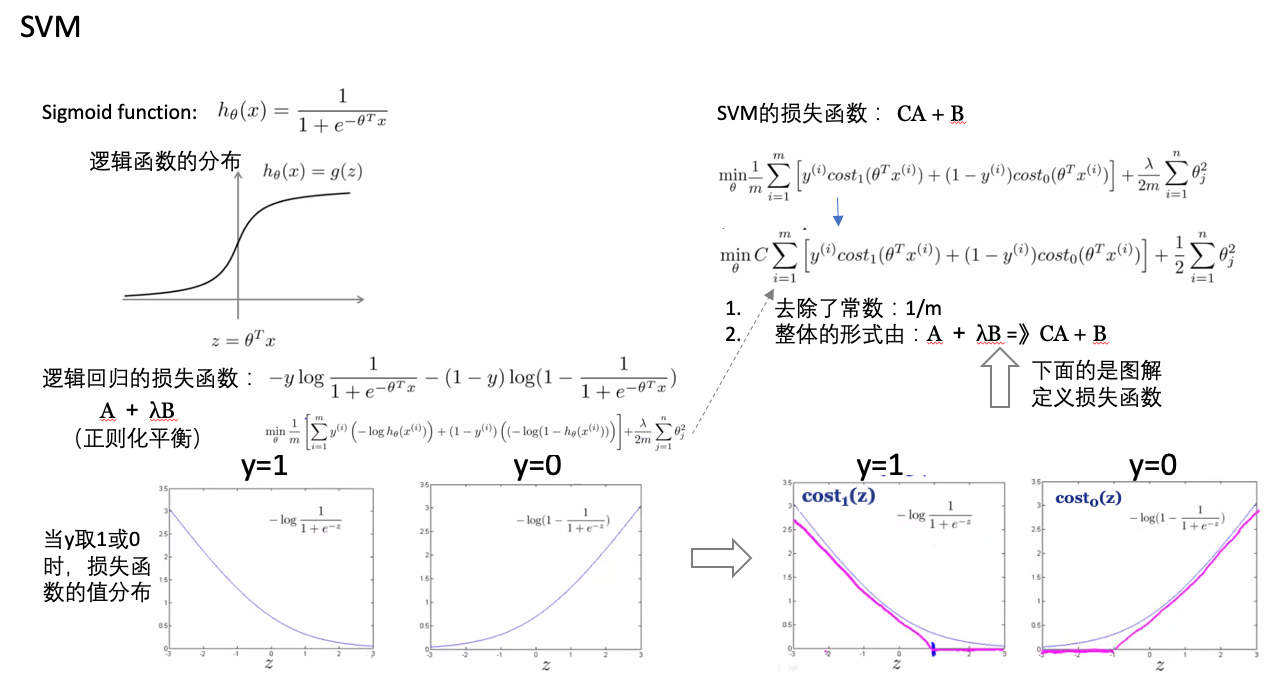
- 损失函数:
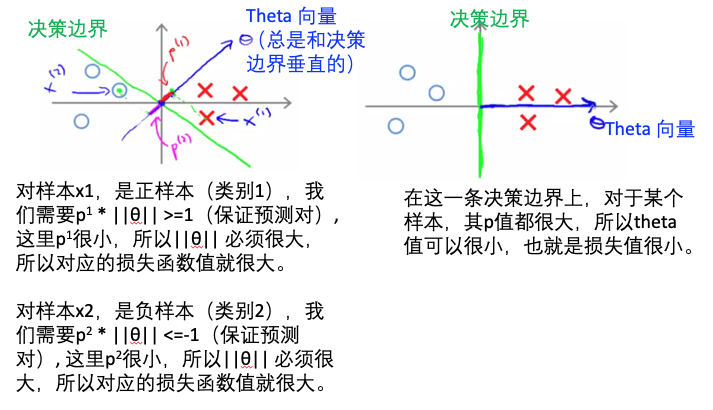
- SVM vs logistic regression决策边界的比较:
- 与逻辑回归相比,SVM是更稳健的,因为其选择的是最大距离(large margin),比如下图中逻辑回归选择了黄绿的边界,能够将现有数据分隔开,但是泛化能力差;黑色的是SVM选择的边界(最大化距离)。
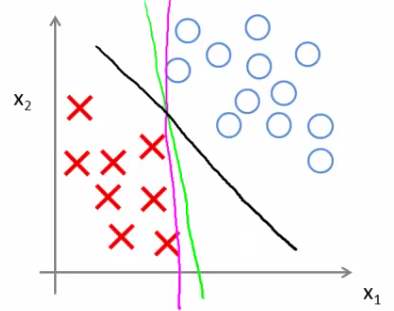
- 与逻辑回归相比,SVM是更稳健的,因为其选择的是最大距离(large margin),比如下图中逻辑回归选择了黄绿的边界,能够将现有数据分隔开,但是泛化能力差;黑色的是SVM选择的边界(最大化距离)。
- 核(kenel):
- 多项式拟合hθ(x) = θ0+ θ1 x f1+ θ2 x f2 + θ3 x f3:
- f1=x1, f2=x1x2, f3=… ,基于特征的组合进行多项式拟合(指定的组合特征向量再乘以权重矩阵)。
- h(x)=1,x<=0
- h(x)=0, x>0
- 多项式拟合计算消耗太大
- 对于空间中,选取某些点作为landmark(这些点是怎么选取的?随机的?),然后对于某个数据点(样本),计算数据点到landmark点之间的距离(相似性),比如用高斯核,计算的这个距离就是欧式距离。
- 相似性函数(similarity function):称为核
- 高斯核:
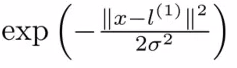
- 如果x距离landmark点很近,那么f1=e(-0)=1; 如果x距离lanmark点很远,那么f1=e(-large number)=0.
- 所以核函数就是定义某个点x距离landmark点的远近的,很近的时候值为1,很远的时候值为0。比如下面的例子是选择landmark点为[5,3],其他x1,x2值时距离此点的远近。
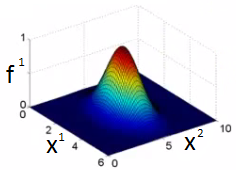
- 多项式拟合hθ(x) = θ0+ θ1 x f1+ θ2 x f2 + θ3 x f3:
- 基于核函数的非线性模型:
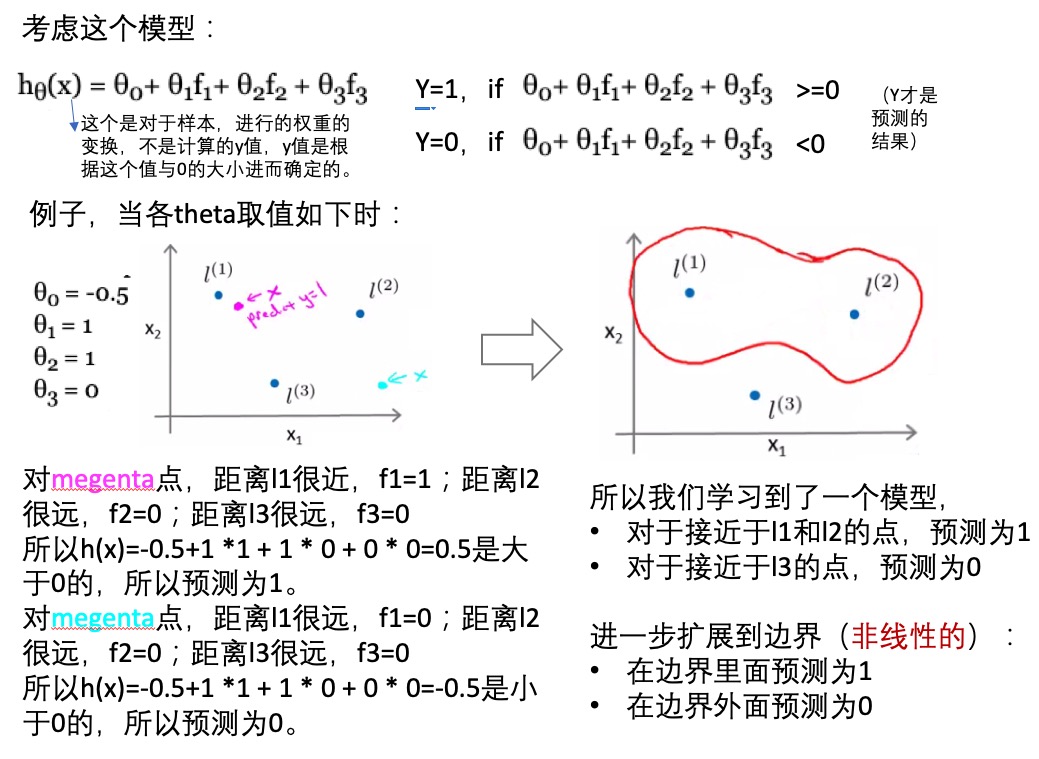
- 如何选取landmark(训练集全都放置一个):
- 对于训练集的每个样本,在其相同的位置放一个landmark,所以总共会有m个landmark
- 对于每个训练样本,计算特征向量:f0,f1,。。。,fm,其中恒有f0=1。有一个fi就是这个样本自己(因为上一步是每个样本都放置了一个landmark),此时fi=1。
- m个feature + f0 =》得到一个特征向量举证:[m+1, 1]维度的
- SVM训练:
- 现在有了特征向量,还有权重矩阵,如果他们的内积是>=0的,则预测的y=1,否则预测为y=0。所以现在需要训练得到权重矩阵!!!
- 有多少个样本m,就有多少个特征
- 使用之前提到的损失函数,训练的到最优的参数(权重矩阵)。在这里是对特征向量f进行优化,而不是原来的x。【xi =》fi,原来的i个特征值变成现在的与各个landmark点的距离远近】
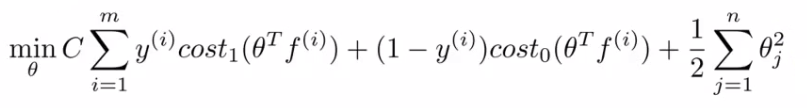
- SVM参数C(CA+B):
- 与正则化里面的1/lambda功能类似,平衡bias和variance
- 小的C:low bias high variance -》过拟合
- 大的C:high bias low variance -》欠拟合
- SVM参数σ2:
- 是在计算特征值f时用到的
- 小的σ2:特征值差异很大,low bias high variance
- 大的σ2:特征值差异较平滑,high bias low variance
- 高斯核:
- 需要定义方差σ2
- 什么时候使用高斯核:特征数n少或者样本数m大
- 在使用之前,必须进行特征缩放。【不然具有大值的特征会主导计算的特征值】
- 线性核:
- 当样本数m小,特征数n很大时:少样本、多特征
- 没有足够的数据
- SVM的多类别:
- 很多工具都支持
- 或者使用one-vs-all的方式
- 逻辑回归 vs SVM:
- 特征数目(n)相对于训练样本(m)很大时,使用逻辑回归或者SVM的线性核。比如文本分类问题:特征10000,训练集1000.
- 特征数目少(1-1000),样本数中等(10-10000),使用高斯核。
- 特征数目少(1-1000),样本数目很多(50000+):1)SVM+高斯核 =》会很慢;2)可以逻辑回归或者SVM线性核;3)手动的增加或者组合特征,增加特征数目。
- 逻辑回归和SVM线性核很相似:做的事情类似,效果相当
- SVM+多种不同的内核,可以构建非线性模型。很多时候神经网络也可以,但是SVM训练会快很多
- SVM是全局最小值,是凸优化的问题
- 通常难以选择最优算法:1)获取更多的数据;2)设计新的特征;3)算法debug
Read full-text »
半监督学习
2018-11-23
目录
标记样本、未标记样本
- 标记样本:labeled,给出了y值的训练样本,\(D_l=\{(x_1,y_1),...,(x_l,y_l)\}\)
- 未标记样本:unlabeled,类别标记未知的样本,\(D_u=\{(x_{l+1},y_{l+1}),...,(x_{l+u},y_{l+u})\}\)
- 传统监督学习:仅使用\(D_l\)构建模型,\(D_u\)包含信息被浪费
- 若\(D_l\)较小,训练样本不足,模型泛化能力不佳
- 问题:能否在构建模型的过程中将\(D_u\)利用起来?
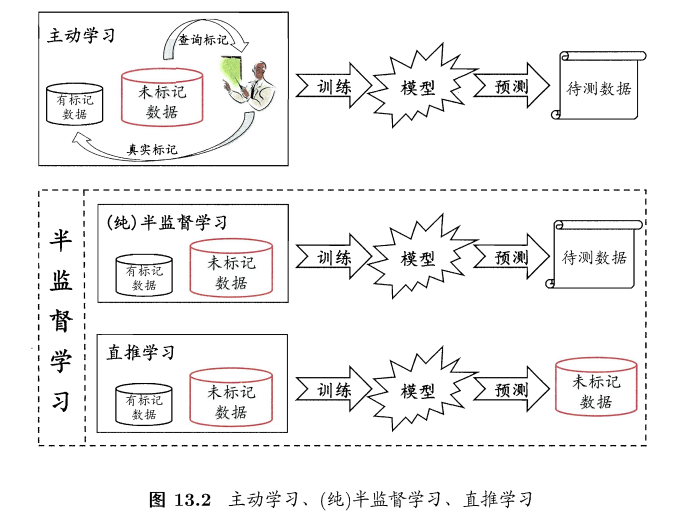
主动学习 vs 半监督
主动学习:active learning
- 引入额外的专家知识,通过与外界的交互来将部分未标记样本转变为有标记样本
- 对于未标记样本,拿来一个,询问专家是好还是坏样本,加入有标记样本数据集进行训练,如果添加的样本能增强模型能力,也可降低标记成本
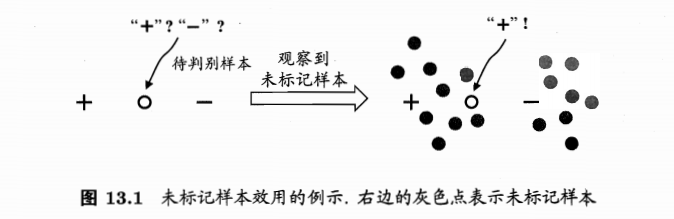
未标记样本的数据分布可提供信息
半监督学习:
- 学习器不依赖外界交互、自动的利用未标记样本提升学习性能
- 显示需求强烈,获取标记很费力
- 利用未标记样本需要一些假设:
- 聚类假设:最常见,假设数据存在簇结构,同一个簇的样本属于同一个类别
- 流形假设:常见,假设数据分布在一个流形结构上,邻近的样本拥有相似的输出值。邻近用相似程度刻画,因此可看做聚类的推广。
- 假设本质:相似的样本拥有相似的输出
分类:
生成式方法
- 基于生成式模型
- 假设所有数据(标记+未标记)由同一潜在模型生成
- 通过潜在模型的参数将未标记数据与学习目标联系起来
- 未标记数据的标记:模型的确实参数
- 可基于EM算法进行极大似然估计
- 不同的潜在模型(人为经验等进行的),对应不同的学习器
为什么未标记样本可以使用上?
- 例子:高斯混合分布的分类
- 预测时的最大化后验概率(对应应该分的类别):

- EM算法求解参数并预测:

- 推广:
- 将这里的混合高斯换为其他的模型,比如混合专家模型、朴素贝叶斯模型,可推导得到其他的生成式半监督学习方法
- 关键:
- 模型假设必须正确,即假设的生成模型必须和真实数据分布吻合,否则使用未标记数据会降低泛化性能
- 现实中难以做出准确假设,借助领域知识
半监督SVM
- 半监督SVM:semi-supervised support vector machine,S3VM
- SVM的推广
- SVM:寻找最大间隔划分超平面
- S3VM:寻找能将两类有标记样本分开,且穿过数据低密度区域的划分超平面
- 基本假设:低密度分隔low-density separation
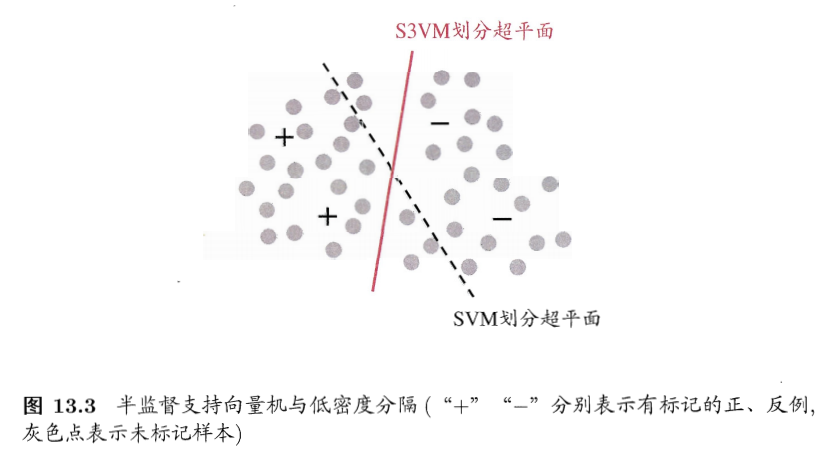
- 基本假设:低密度分隔low-density separation
- TSVM:transductive support vector machine
- 著名的半监督SVM
- 二分类问题
- 对未标记样本进行各种可能的指派(类别1还是类别2),然后在这些所有的可能中,寻求一个在所有样本上间隔最大化的划分超平面。
- 当超平面确定,未标记样本的指派就是其预测结果
- TSVM定义:
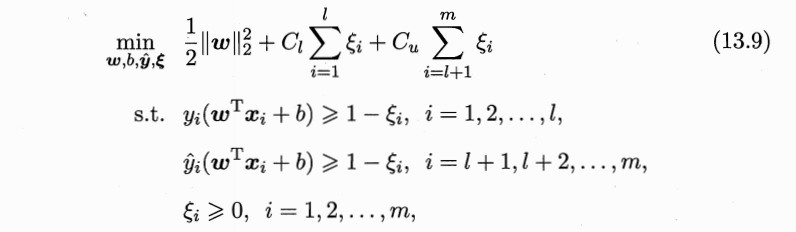
- 划分超平面:\((w,b)\)
- 松弛向量:\(\epsilon\)
- 平衡模型复杂度、有/无标记样本重要性:\(C_l, C_u\)
- 尝试不同的分类情况 =》穷举过程
- TSVM求解:局部搜索迭代
- 使用有标记样本学习一个SVM
- 利用SVM对未标记样本进行分类
- 此时有标记样本+无标记样本都是有标记的,只不过无标记的label是SVM给出的”伪标记“。代入到上面的式子,即可求解划分超平面和松弛向量(此时是个标准SVM问题)。此时”伪标记“不准确,需要提高有标记样本的重要性,所以设置:\(C_u\ltC_l\)
- 找两个label为异类且很可能分错的未标记样本,交换标记,再求解此时的划分超平面和松弛向量。
- 不断迭代,同时提高\(C_u\)的值,增大未标记样本对优化目标的影响
- 直到\(C_u=C_l\)为止

- 如果类别不平衡:将\(C_u\)拆分成\(C_u^+,C_u^-\)
- 缺点:
- 对每一对可能分类错的进行调整
- 计算开销巨大
图半监督学习
- 给定数据集,映射为图
- 结点:数据集的样本
- 边:边的强度对应样本之间的相似性
- 有标记样本:染过色的结点
- 未标记样本:未染色的节点
-
半监督学习:颜色在图上进行扩散或者传播的过程
- 标记传播方法:
- 多分类

- 多分类
基于分歧的方法
- 基于单学习器:生成式、半监督SVM、图半监督式
- 使用多学习器:基于分歧,disagreement-based methods,学习器之间的分歧对于未标记样本的利用至关重要
- 代表:协同训练(co-trainning),也是多视图学习的代表(multi-view learning)
- 多视图数据:
- 一个数据对象往往有多个属性集
- 每个属性集构成一个视图
- 例子:电影
- 图像画面信息属性集
- 声音信息属性集
- 字幕信息属性集
- 网上宣传信息属性集
- 电影样本:\(((x^1, x^2),y)\),\(x^1\)是图像属性向量,\(x^2\)是声音属性向量
- y是标记:影片类型
- 不同视图具有兼容性:即通过不同的属性预测的类别标记是兼容的,不能一个属性预测出的标记是另一个属性预测出来不涵盖的类别。即:\(y=y^1=y^2\)
- 因此不同的属性预测出的是样本不同的类别的信息
- 相容性基础上,不同视图的互补信息会给学习器构建带来便利
- 协同训练:
- 数据具有充分独立视图
- 充分:每个视图足以产生最优学习器
- 独立:视图是独立的
- 训练过程:
- 在每个视图上分别训练出一个学习器
- 每个学习器分别挑出自己最有把握预测对的未标记样本,赋予标记。将这个样本给另一个学习器作为有标记样本进行训练,以更新模型。
- ”相互学习,共同进步“
- 不断迭代,直到学习器不再变化为止

- 数据具有充分独立视图
- 适用:
- 采用合适的基学习器
- 数据不具备多视图时,需要巧妙设计
半监督聚类
- 聚类的监督信息有两种:
- 必连和勿连约束:必连 =》样本必须在同一个类里,勿连=》样本必须不在同一个类里
- 少量的有标记样本
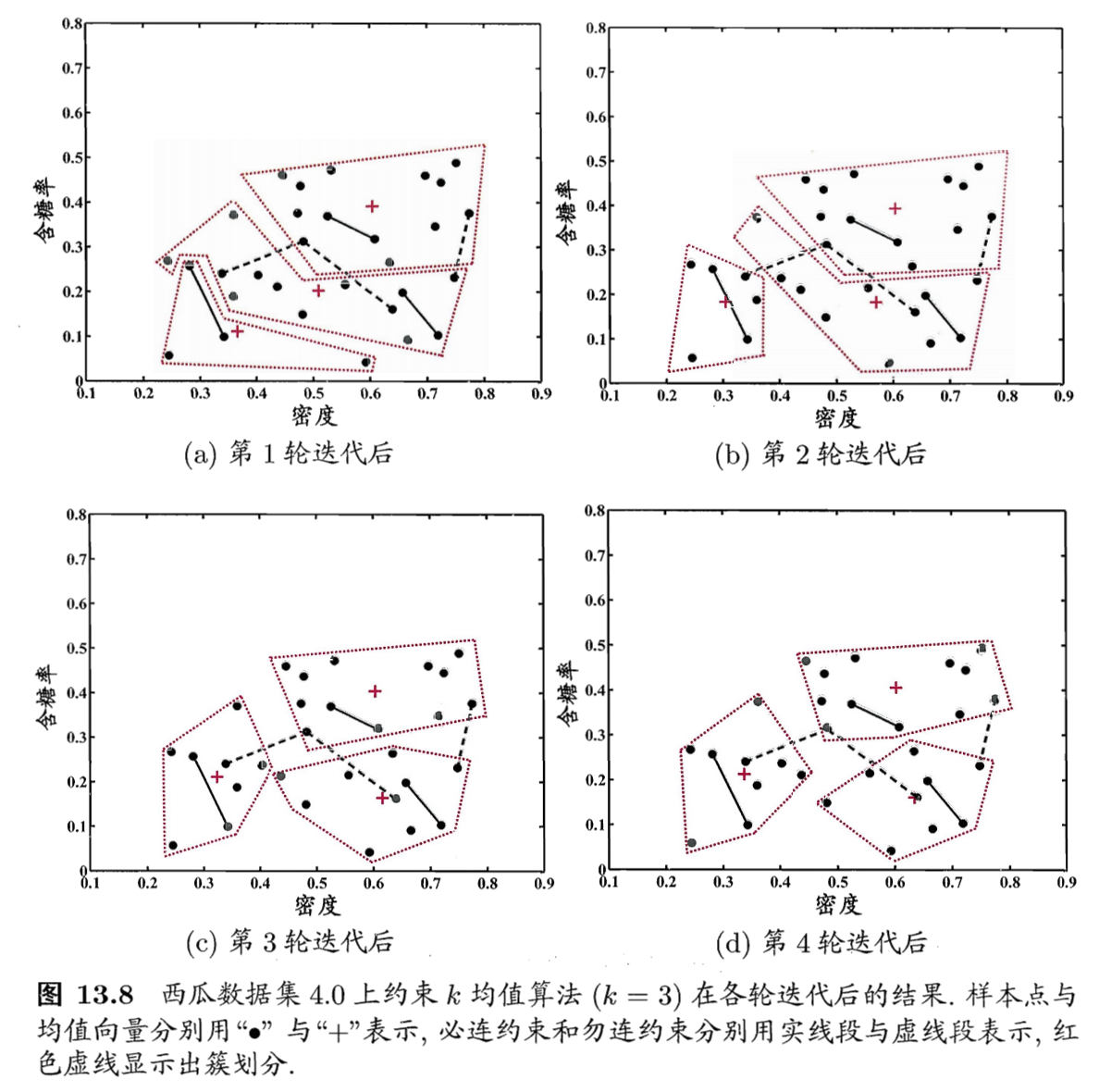
- 约束K均值聚类:
- 利用必连和勿连约束的代表
- 算法过程:

- 西瓜数据集的聚类结果:
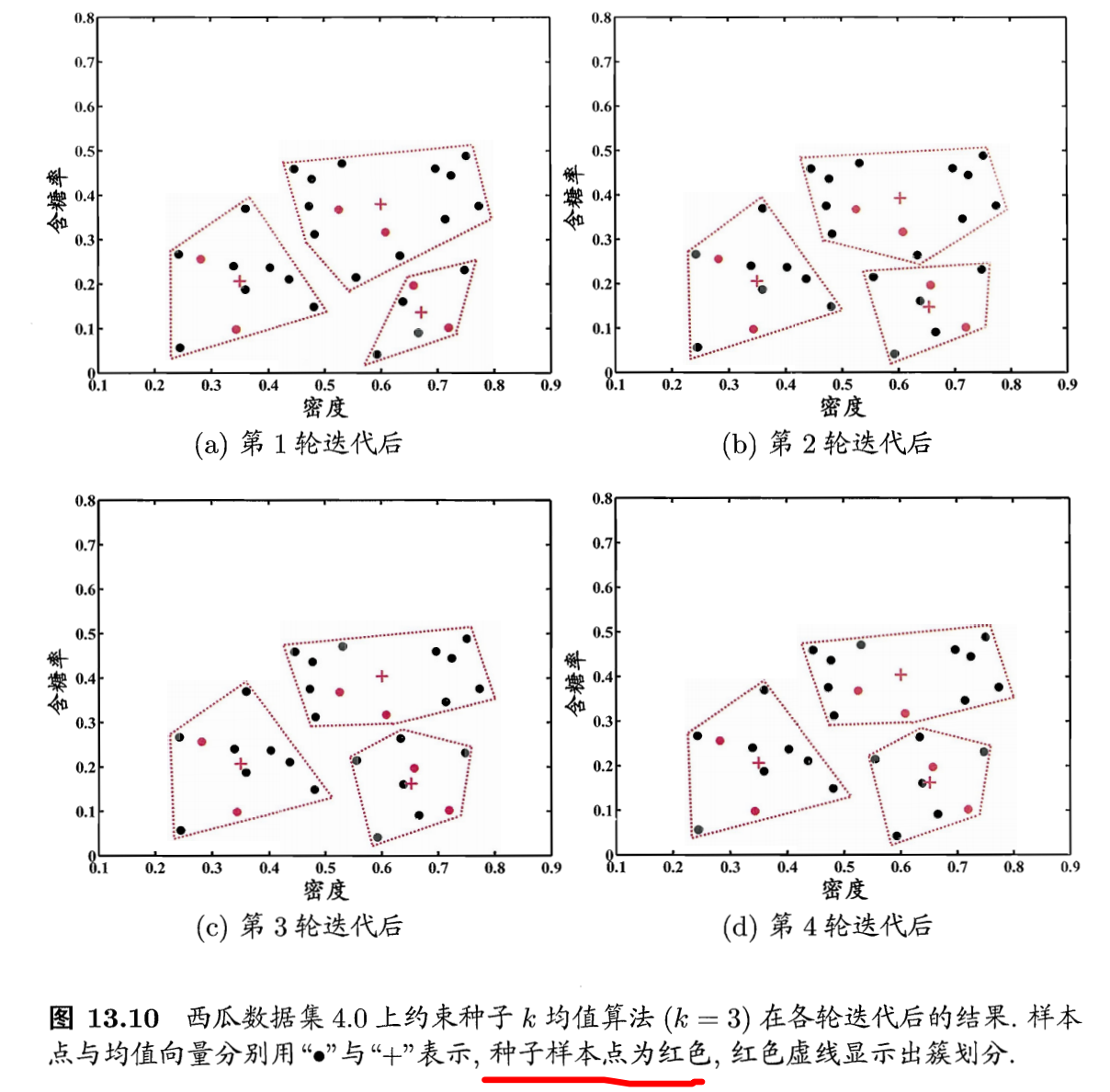
- 约束种子k均值聚类
- 利用少量有标记样本的信息
- 少量的有标记样本,其类别是知道的
- 将有标记样本作为种子,用他们初始化k个聚类中心
- 同时在迭代过程中不改变种子的所属类别关系
- 算法过程:

- 西瓜数据集的聚类结果:
参考
- 机器学习周志华第13章
Read full-text »
[CS229] 11: Machine Learning System Design
2018-11-20
11: Machine Learning System Design
- 垃圾邮件检测:
- 监督学习:单词作为特征
- 收集数据,email头信息提取特征,正文信息提取特征,错误拼写检测
- 误差分析:
- 实现简单模型,测试在验证数据集上的效果
- 画学习曲线,看数据量、增添特征能否提升模型性能
- 误差分析:focus那些预测错误的样本,看是否有什么明显的趋势或者共同特征?
- 分析需要在验证数据集上,不是测试集上
- skewd class的误差分析:
- precision: # true positive / # predicted positive = # true positive / (# true positive + # false positive)
- recall: # true positive / # actual positive = # true positive / (# true positive + # false negative)
- F1 score = 2 * (Precision * Recall) / (Precision + Recall)
- 在验证数据集上,计算F1 score,并使其最大化,对应于模型效果最佳
- large data rationale: 可以构建有更多参数的模型
Read full-text »
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me