损失函数
2019-02-17
目录
什么是损失函数
- 估量模型的预测值f(x)与真实值Y的不一致程度
- 损失函数越小,一般就代表模型的鲁棒性越好
- 损失函数指导模型的学习
分类损失函数
0-1 loss
-
公式:\(L(y_i, f(x_i)) = \begin{cases} 0& y_i = f(x_i)\\ 1& y_i \neq f(x_i) \end{cases}\)
- 直接比较预测值和真实值是否相等
- 预测和标签相等,值为0(预测很准,loss很小),值为1(预测很不准,loss很大)
- 缺点:无法对x进行求导,所以在深度学习的反向传播中,不能被直接使用(一般用于启发新的loss)
负对数似然损失
- 公式:\(loss(x,f(x)) = -log(f(x))\)
- 惩罚预测的概率值小的,激励预测的概率值大的
- 预测的概率值越小,对数log值的值越小(负的越多),加一个负号,就是值越大,那么此时的loss也越大
- pytorch:
torch.nn.NLLLoss
交叉熵
- 熵:物理学上表示一个热力学系统的无序程度
- 信息熵:
- 信息的量化度量,由香农提出
- 对数函数表示对不确定性的测量
- 熵越高,表示能传输的信息越多,熵越少,表示传输的信息越少。熵 =》信息量
- 原理:每个信息都存在冗余,冗余的大小与符号的出现概率或者不确定性有关。出现概率大,则不确定性小,可用对数函数表征。
- 为什么对数函数?
- 不确定性必须是出现概率的单调递减函数
- 离散的独立事件,其总的不确定性等于各自不确定性之和
- 不确定性:\(f=log(\frac{1}{p})=-log(p)\)
- 信息熵:
- 单个符号的不确定性的统计平均
- 公式:\(-\sum_{i=0}^{n} p_ilog(p_i)\)
- 分类交叉熵:
- 所有样本在每个类别的信息熵的总和
- 公式:\(l(f, y)=-\sum_{i}^{n}\sum_{j}^{m}y_{ij}logf(x_{ij})\)
- 参数
n:样本数量 - 参数
m:类别数量 - 参数 \(y_{ij}\):第
i个样本属于分类j的标签,它是0或者1 - 参数 \(f(x_{ij})\):样本
i预测为j分类的概率
- 特点:
- 主要用于学习数据的概率分布
- 像MSE等是惩罚预测错误的,交叉熵对于高可信度预测错误的会有更大的惩罚
- 负对数损失:不会根据预测的可信度进行惩罚;交叉熵:也会惩罚预测错误且可信度很高的,或者预测正确且可信度很低的
- pytorch:
torch.nn.CrossEntropyLoss
softmax loss
- 如果上面的\(f(x_{ij})\)是softmax概率的形式(指数概率),此时就是softmax with cross-entropy loss,简称softmax loss
- softmax loss是交叉熵的一个特例
- 分类分割任务
- 不平衡样本:weighted softmax loss, focal loss
- 蒸馏学习的soft softmax loss
KL散度
- 估计两个分布的相似性
- 公式:\(D_{kl}(p\mid q) = \sum_{i} p_i log(\frac{p_i}{q_i})\)
- 当p和q处处相等时,上式才=0,即分布相同
- 变形:\(D_{kl}(p\mid q) = \sum_{i} (p_i logp_i - p_i logq_i) = -l(p,p) + l(p,q)\)
l(p,p):p的熵,当一个分布一定时,熵为常数值l(p,q):p和q的交叉熵- KL散度和交叉熵相差一个常数值,所以用哪个作为loss都是可以的,最小化交叉熵也是最小化KL散度
- 不是根据预测的可信度进行惩罚(这是交叉熵要做的),而是根据预测和真实值的差异进行惩罚
- 注意:KL的非对称性,\(D_{kl}(p\mid q) \neq D_{kl}(q\mid p)\)
- pytorch:
torch.nn.KLDivLoss
hinge loss
- 主要用于SVM,解决间距最大化问题
- 公式:\(l(f(x), y) = max(0, 1-yf(x)) = \begin{cases} 0& y_i = f(x_i)\\ 1& y_i \neq f(x_i) \end{cases}\)
hinge embedding loss
- 用于衡量两个输入是否相似或者不相似
- 公式:\(l_n = \begin{cases} x_n& y_n = 1\\ max\{0, margin - x_n\}& y_n = -1 \end{cases}\)
- margin: default = 1
- pytorch:
torch.nn.HingeEmbeddingLoss
指数损失与逻辑损失
- 指数形式,梯度比较大,主要用于Adaboost集成学习中
- 公式:\(l(f(x), y) = e^{-\beta y f(x)}\)
- 取对数形式:\(l(f(x), y) = \frac{1}{ln2} ln(1+e^{-yf(x)})\),梯度相对平缓
Cosine Embedding Loss
- 对于两个输入x1,x2,根据标签计算其cos相似性的loss
- 公式:\(l(f(x), y) = \begin{cases} 1-cos(x1,x2) & y = 1\\ max\{0, cos(x1,x2) - margin\}& y = -1 \end{cases}\)
- 相似性:\(similarity = cos(\theta) = \frac{A * B}{\mid A\mid \mid B\mid}\)
- 默认时marign=0
- 当y=1时,loss=1-cos(x1,x2)
- 当y=-1时,loss=max{0, cos(x1,x2)}。如果cos(x1,x2)>0,loss=cos(x1,x2);如果cos(x1,x2)<0,loss=0.
- pytorch:
torch.nn.CosineEmbeddingLoss
回归损失函数
L1 loss | MAE
- 以绝对误差作为距离
- Mean absolute loss,MAE
- 公式:\(l(f(x), y) = \mid y - f(x) \mid\)
- 具有稀疏性,常作为正则项添加到其他loss中,可以惩罚较大的值
- 问题:梯度在零点不平滑,导致会跳过极小值
- pytorch:
torch.nn.L1Loss
L2 loss | MSE | 均方差 | 平方损失
- 欧氏距离:以误差的平方作为距离
- Mean Squared Loss/Quadratic Loss,MSE loss
- 公式:\(L2=MSE=\frac{1}{n} \sum_{1}^n(y_i - \overline{y_i})\)
- 平方使得放大大的loss,当模型范大的错误就惩罚它
- 也常常作为正则项
- 当预测值与目标值相差很大时, 梯度容易爆炸,因为梯度里包含了x−t。
- pytorch:
torch.nn.MSELoss
smooth L1 loss | Huber loss
- L1/L2 局限:
- L1:梯度不平滑
- L2:容易梯度爆炸
- 新的综合两者有点的loss
- 公式:\(smooth_{L1} (x, f(x)) = \begin{cases} 0.5(x-f(x))^2& , \mid x-f(x)\mid < 1\\ \mid x-f(x)\mid -0.5& , otherwise \end{cases}\)
- 当x-f(x)较小时,等价于L2 loss,保持平滑
- 当x-f(x)较大时,等价于L1 loss,可以限制数值的大小
- 与MSE相比,对于outliner更不敏感,当真实值和预测值差异较大值,此时类似于L1 loss,不像MSE loss的平方,所以可避免梯度爆炸
- pytorch:
torch.nn.SmoothL1Loss
GANs
Margin Ranking Loss
- 对于两个输入x1,x2,以及一个标签y(取值1和-1的tensor),评估x1和x2的排序
- 当y=1,x1的排序高于x2
- 当y=-1,x1的排序低于x2
- 公式:\(loss(x, y) = max(0, -y * (x1-x2) + margin)\)
- 如果x1、x2的排序和数据是吻合的,那么此时y * (x1-x2)是大于0的,-y * (x1-x2) + margin是小于0的,整个loss取值为0.
- 如果x1、x2的排序和数据是不吻合的,那么此时y * (x1-x2)是小于0的,-y * (x1-x2) + margin是大于0的,整个loss取值为大于0的一个值,相当于对这种错误的预测有一个惩罚.
- pytorch:
torch.nn.MarginRankingLoss
参考
Read full-text »
【3-2】机器学习(ML)策略(2)
2019-02-13
目录
- 目录
- 进行误差分析
- 清除标注错误的数据
- 快速搭建第一个系统进行迭代
- 使用不同分布的数据进行训练和测试
- 数据分布不匹配时的偏差和方差分析
- 处理数据不匹配问题
- 迁移学习
- 多任务学习
- 端到端的深度学习
- 是否使用端到端的深度学习?
- 参考
进行误差分析
- 误差分析:人工检查一下你的算法犯的错误,可以了解接下来应该做什么
- 例子:猫识别
- 准确率90%,错误率10%。注意到有的狗的图片被错误识别为猫,是否应该花时间处理狗识别错误这个问题?
- 做法:收集100个开发集样本,手动检查,数出总共有多少个样本是狗。
- 假如5%是狗:如果花时间解决,错误率从10%下降到9.5%,错误率相对下降5%。此时改进并不是很大。
- 假如50%是狗:如果花时间解决,错误率从10%可能下降到5%。此时可以花时间解决这个。

- 对于算法改进的性能上限是多少,最好能到哪里,完全解决狗的问题有多少帮助。
- 同时评估多个想法:
- 上面是说错误来自于把狗识别为猫
- 假如同时存在其他的可能性呢?比如猫科动物的错误识别,图像模糊等
- 做法:通过错误分析同时评估这些个想法。
- 具体:建立一个表格,对于想要看的数据集,一个个的看,看是否存在潜在想法的,有就对应栏目+1,最后统计出算法在这个数据集上,每一个想法的错误的百分比。基于此,就知道哪个想法所占的错误比例最大,也是最有可能在进行改进后提升模型效果的。
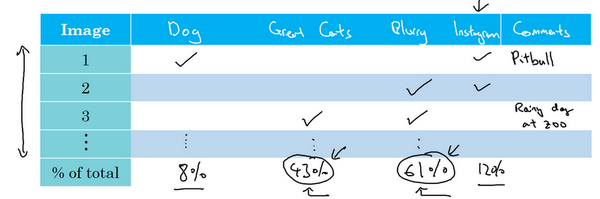
- 中途添加新的想评估的想法:
- 在人工看每个数据集的时候,有时候会出现新的错误原因,可以再列举出来,和其他想法一起查看
- 错误分析:通过快速统计,统计出不同错误标记类型占总数的百分比,可以帮助发现哪些问题需要优先解决(高低的优先级),或者为构思新优化方向提供灵感
清除标注错误的数据
- 如果有的数据标签是错的,是否值得花时间去修正
- 分情况(训练集):
- 随机错误:不用花时间修复,因为深度学习算法对于训练集中的随机错误是很健壮的,如果这些错误标注的样本离随机样本不太远
- 系统错误:学习算法不健壮
- 比如一直把白色的狗标记为猫,这就会带来学习的问题
- 开发集、测试集:
- 使用错误分析,看开发集和测试集中的例子
- 如果错误标记比例大,严重影响开发集上评估算法的能力,需要花时间去修复
-
如果不影响评估,可不花时间去处理
- 例子:
- 错误率10%,6%来自于标记出错,那么10%*6%=0.6%的错误来自于标记,其他原因占比9.4%,应该看其他的什么原因主导错误
- 错误率2%,0.6%来自于标记出错,其他原因1.4%。但是此时0.6%/2%=30%是由于标记出错的,此时去处理这些错误标签是值得的。

- 如何清除:
- 同时修正开发集和测试集:保证来自于统一分布
- 同时检验算法判断正确和错误的样本
- 训练集数据与开发集或者测试集稍微不同,也没关系,模型是比较健壮的

快速搭建第一个系统进行迭代
- 快速建立系统:
- 设立开发集、测试集和评估指标:决定了目标所在,即使目标定错了,也是可以后面更改的
- 训练集进行训练:看效果,理解算法的表现
- 意义:
- 快速而粗糙的实现
- 确定偏差方差范围
- 错误分析:确定优化方向

使用不同分布的数据进行训练和测试
- 例子:
- 任务:猫识别任务
- 数据:20000网络抓取(高质量),10000用户提供(低质量)
- 核心:最后app是处理用户新提供的数据的,所以这里和最后实际的而应用场景相同的数据分布的就只有10000个样本,其余200000网络的样本不是相同分布,如何做?
- 问题:如何进行数据的划分?
- 方案1:总共210000张,合并后随机打乱,分成训练、开发和测试集:205000,2500,2500。
- 不好:2500个样本,平均有多少个用户上传的图片:2500-2500*(200k/210k)=119。这个样本数量的开发集中含有的靶标数据(用户上传的图片)太小了,所以实际是在对不关心的数据分布做优化。
- 方案2:训练集:200000+5000用户,开发和测试各2500,此时开发集包含的数据全部来自于用户,而这正是需要真正关心的图片的分布。
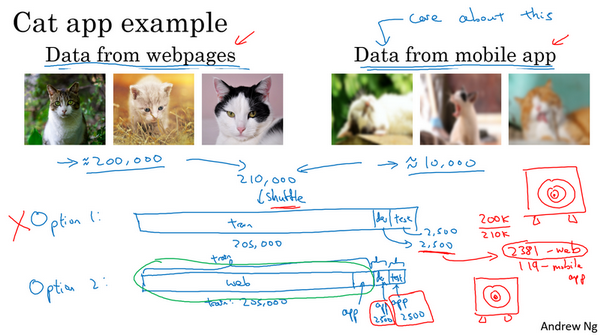
- 虽然此时训练集和开发集、测试集分布不一样,但是事实证明这样的划分,在长期能带来更好的性能
- 例子:
- 任务:语音后视镜激活
- 训练集:可以来自不同的来源,购买的,其他设备的
- 开发和测试集:必须是语音激活的数据集,这个是和任务最相关的,也是设定的目标
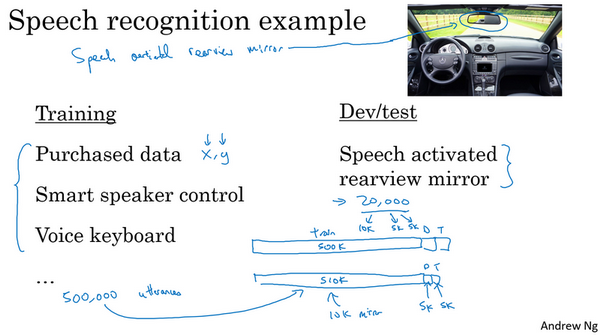
数据分布不匹配时的偏差和方差分析
- 数据同分布:
- 贝叶斯错误率:0%
- 训练误差:1%
- 开发误差:10%
- 结论:这里方差很大,模型泛化能力不好。能很好的处理训练集,但是在开发集上效果很差。
- 数据不同分布:
- 贝叶斯错误率:0%
- 训练误差:1%
- 开发误差:10%
- 结论:不能得出方差很大的结论。
- 原因:可能训练集图片更容易识别,所以训练集效果好,开发集差
- 核心:两件事情变了
- 算法只见过训练数据,没见过开发数据
- 开发集数据来自于不同的分布
- 所以难以判断增加的9%的误差,是因为没见过开发数据(泛化能力),还是因为开发集数据分布本身就不一样。
- 哪个因素影响更大?
- 解决:引入训练-开发集
- 训练-开发集:
- 随机打散训练集,然后拿出一部分训练集作为训练-开发集
- 此时训练集、训练-开发集来自同一分布
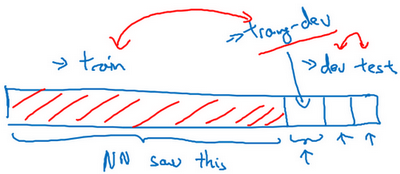
- 例子:
- 左边:训练误差1%,训练-开发误差9%,开发误差10%【存在方差问题,因为训练-开发错误率是和训练同一分布得到的,泛化能力本身就不好】
- 右边:训练误差1%,训练-开发误差1.5%,开发误差10%【数据不匹配问题,因为在同分布的训练-开发上错误率很小,但是在不同分布的开发上错误率很高】
-
数据不匹配问题:算法擅长处理和你关心的数据不同的分布

- 左边:存在可避免偏差,算法比人的水平差很多
-
右边:可避免偏差+数据不匹配问题

- 原则:查看人类平均错误率、训练集错误率、训练-开发集错误率,以确定可避免偏差、方差、数据不匹配问题大小

- 开发测试错误率比人的更低?
- 人4%,开发测试6%,为什么?
- 如果开发测试集分布比应用实际处理的数据要容易得多,那么这些错误率可能会降低。
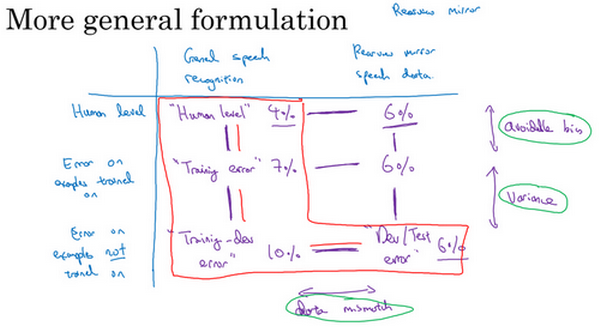
- 偏差方差分析:
- 普适的分析
- 建立表格:水平轴是不同的数据,纵轴是标记数据的方式或者算法(比如这里是语音数据的不同来源)。然后看不同的数据在不同的数据集上的错误率大小。
- 可避免偏差:human vs train
- 方差:train vs train-dev
- 数据不匹配:train-dev vs dev/Test
- 系统解决数据不匹配的方法不存在,但是可以做一些尝试
处理数据不匹配问题
- 如何处理数据不匹配?
- 错误分析:
- 了解训练集和开发测试集的具体差异
- 为了避免对测试集过拟合,要做错误分析,应该人工去看开发集而不是测试集
- 收集更多的数据,使得训练数据和开发集数据越来越像
- 如何做到?
- 策略:人工合成数据
- 比如知道训练集其实是更干净的数据,可以人工合成具有噪声的数据作为训练集
- 有名的语音例子:The quick brown fox jumps over the lazy dog。【含有a-z的所有字母】
- 人工合成风险:
- 数据对于噪声的过拟合
-
如果语音的数据很多,但是真实的噪声数据很少,在组合之后,其实噪声数据集还是小,只模拟了全部数据空间的一小部分,容易使得模型过拟合。

- 汽车识别例子:
- 后两个汽车图片是合成的,如果汽车是有限的,也容易陷入过拟合

迁移学习
- 深度学习概念:神经网络从一个任务中析得知识,并将这些知识应用到另一个独立的任务中
- 例子:
- 动物图像识别 =》 X射线图像识别
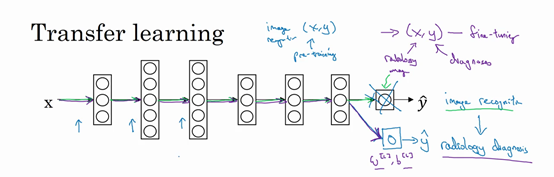
- 如何做?
-
把神经网络最后的输出层拿走,以及进入最后一层的权重删掉,然后为最后一层重新赋予随机权重,让它在X射线图像数据上训练
- 经验:
- 如果有一个小数据集,就只训练输出层前的最后一层,或者最后一两层
-
如果有足够多的数据,可以重新训练网络中的所有参数
- 预训练:pre-training,如果重新训练神经网络的所有参数,那么这个在图像识别数据的初期训练阶段,称为预训练。用图像识别数据去预先初始化神经网络的权重。
- 微调:fine tuning,如果以后更新所有权重,然后在X射线数据上训练,这个过程就是微调。
- 动物图像识别 =》 X射线图像识别
- 为什么可以迁移?
- 低层次特征能够学习到:边缘检测、曲线检测、阳性对象检测
- 可以帮助学习更快或者只需要更少的数据
- 应用场景:
- 在迁移来源问题中有很多数据,但是迁移目标问题没有那么多数据
- 比如图像识别有1000000样本,X射线识别只有100个样本
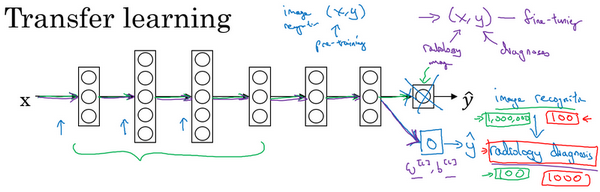
- 语音识别有10000小时样本,唤醒词检测只有1小时数据
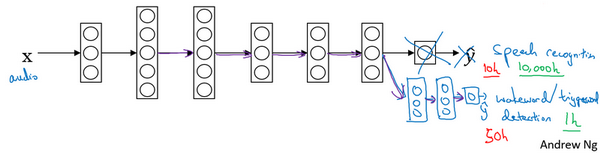
- 注意:反过来可能不起作用,即数据量少的问题迁移到数据量很多的问题。样本不能cover到,有用的样本训练时没有用上。
- 什么时候迁移学习是有效的?
- 两个学习任务的输入是一样的
- 任务A的数据比任务B多得多
- 任务A的低层次特征,可以帮助任务B的学习
多任务学习
- 迁移学习:串行的,从任务A中学习知识然后迁移到任务B上
- 多任务学习:试图让单个神经网络同时做几件事情,然后希望这里每个任务都能帮助到其他所有任务
- 例子:
- 研发无人驾驶车辆
- 同时检测:行人、车辆、停车标志、交通灯
-
这本可以是四个不同的检测任务

- 网络结构:预测的输出就是一个多维向量,比如这里是4x1的向量
-
损失函数:单个样本时,是对这四个分量的求和
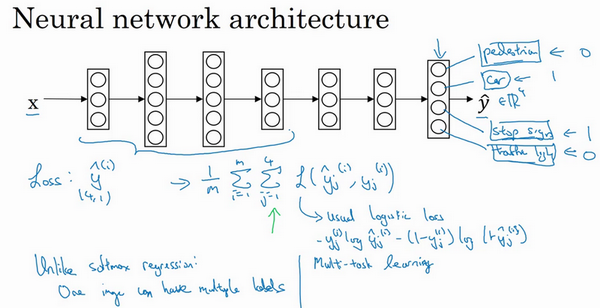
- 做法:建立单个神经网络,观察每张图,解决四个问题,告诉每个图里有没有这四个物体
- 早期特征,在识别四个物体中都是用到的,所以一个神经网络比单独训练四个完全独立的性能要好
- 多任务学习的确实数据?
- 对于训练数据,不一定每个任务都有对应的标签
- 此时这些数据也是可以进行多任务学习的
- 在损失求和时,对于那些确实的(问号的)项,忽略掉即可
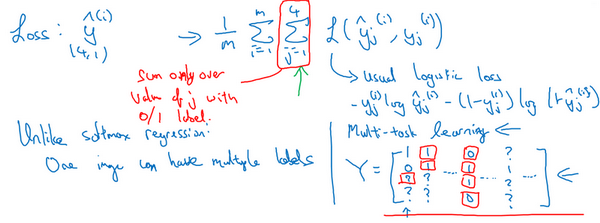
- 什么时候多任务学习有效?
- 这组任务可以共用低层次特征。比如上面的无人驾驶,物体的识别具有一些相似的低级特征
- 每个任务的数量很接近,或者说其他任务加起来的数据量比单个任务大得多。这样,学习的时候其实是无形中增大了数据集。
- 可以训练一个足够大的网络。
- 多任务学习性能低于单个任务的情况:训练的神经网络不够大。当足够大时,多任务学习肯定不会降低性能。
- 迁移学习 vs 多任务学习:
- 迁移学习:使用频率更高
- 多任务学习:使用频率较低。难以找到那么多相似数据量对等的任务可以用单一神经网络训练。例外:物体检测任务。
端到端的深度学习
- 传统机器学习 vs 端到端:
- 传统:需要多个阶段
- 端到端:忽略所有不同的阶段,用单个神经网络代替它
- 例子:语音识别
- 传统:语音,提取特征,音位,单词,文本
- 端到端:直接从语音到文本
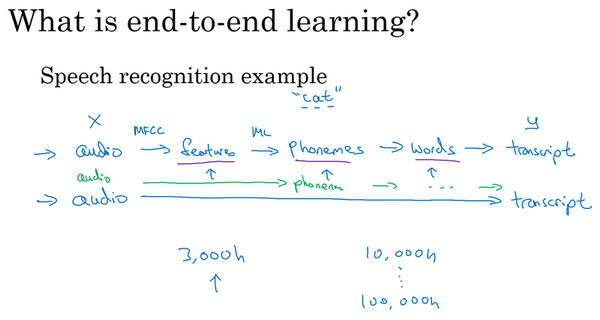
- 挑战:
- 需要大的数据量
- 如果语音识别,数据量不大,比如2000小时,可能流水线的方式更好
- 如果语音识别,数据量很大,比如100000小时,那么端到端的效果通常更好
- 例子:
- 百度的门禁系统
- 分步:定位人脸+判断人脸身份,每一步的数据量都很多,问题也很明确简单。所以现在采用这种分步的方法效果更好。
- 端到端:拍照到身份,数据量太少
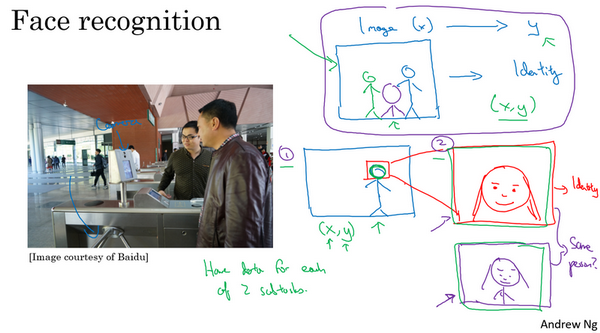
是否使用端到端的深度学习?
- 优点:
- 只看数据。数据很多时,可以捕捉任何的统计信息,不会被迫引入人类的偏见。
- 所需手动设计的组件更少。简化设计流程。
- 缺点:
- 需要大量的数据
- 排除了可能有用的手工设计组件
- 核心问题:
- 是否有足够的数据能够学到从x映射到y的足够复杂的函数?
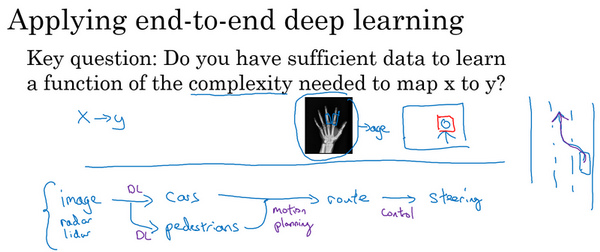
- 是否有足够的数据能够学到从x映射到y的足够复杂的函数?
- 例子:
- 无人驾驶
- 拍照,检测物体,规划路线等多个步骤
- 前面的检测也许深度学习可以做的很好,但是后面的运动路径不是深度学习能完成的。
- 多步的方法比端到端更好
- 纯粹的端到端的深度学习,前景不如更复杂的多步方法,目前收集的数据,训练神经网络的能力是有限的。
参考
Read full-text »
【3-1】机器学习(ML)策略(1)
2019-02-09
目录
- 目录
- 为什么是机器学习策略?
- 正交化
- 单一数字评估指标
- 满足指标和优化指标
- 训练集、开发集、测试集的分布
- 开发集和测试集的大小
- 什么时候该改变开发集/测试集合评估指标?
- 为什么跟人的表现进行对比?
- 可避免偏差
- 理解人的表现
- 超越人的表现
- 改善模型表现
- 参考
为什么是机器学习策略?
- 目标:学习如何更快速高效的优化你的机器学习系统
- 例子:
- 目标:猫分类器
- 当前效果:90%准确性;需要改善
- 尝试:
- 收集更多数据
- 更多样化的反例
- 训练更久的梯度下降
- 其他的优化算法如Adam
- 不同规模的神经网络
- dropout或者正则化

- 错误的尝试怎么办?
- 策略:
- 分析机器学习问题的方法
- 指引朝着最有希望的方向前进
正交化
- 正交化:效率很高的机器学习专家有个特点,就是思维清晰,对于要调整什么来达到某个效果,非常清楚,这个步骤就是正交化
- 例子:
- 电视图像的调节:
- 一个按钮调整高度
- 一个按钮调整宽度
- 一个按钮调整旋转角度
- 每一个按钮都有相对明确的功能,只能调整一个性质,这样调整电视图像会容易得多
- 开车:
- 方向盘:左右偏移
- 油门:速度
- 刹车:速度
- 电视图像的调节:
- 正交化概念:某一个维度,只改变某一个性质,这样在理想的情况下和实际想控制的性质一致,调整参数就容易得多。
- 机器学习的正交化:
- 调整模型的按钮,使得满足4点,如果哪点不满足,可以采取对应的能使得满足的策略,而不影响其他已经满足的点:
- 【1】在训练集上结果不错。可能策略:训练更大的网络、更好的优化算法。
- 【2】在开发集上有好的表现。可能策略:引入正则化、增大训练集。
- 【3】在测试集上也有好的表现。可能策略:对开发集过拟合,需要使用更大的开发集。
-
【4】在真实数据集上表现满意。可能策略:改变开发集或者成本函数

- 一般不使用early stop策略:难以分析,早起停止,对于训练集拟合不够好,同时能改善开发集表现,不是绝对的正交化。
单一数字评估指标
- 单实数评估指标:
- 快速告诉你所做的尝试是不是效果更好
- 例子:猫的识别
- 可以使用准确率和召回率评估模型的效果
- 但是如果是两个指标,一个指标在A比B好,另一个指标在B比A好,那么A和B到底谁好?
- F1分数:准确率和召回率的调和平均数(\(F_1=\frac{2}{\frac{1}{P}+\frac{1}{R}}\))
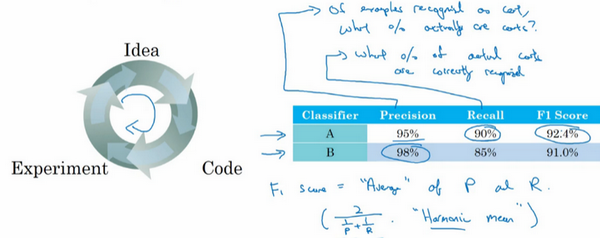
- 最好找一个单实数评估指标,以选择模型,能提高模型迭代的效率
- 例子:分类器在不同的测试集上表现不同
- 在不同的地区错误率不一样
- 哪个分类器效果好?
- 平均值:假设平均值是一个合理的单实数评估指标,通过计算平均值,可以快速判断。
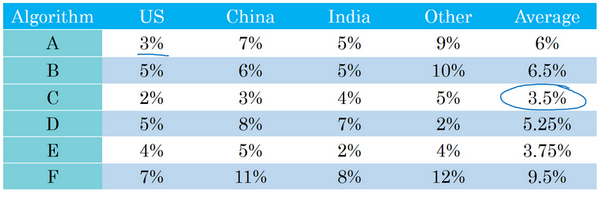
- 可以看到,C分类器的平均错误率最低,可以选用这个算法
满足指标和优化指标
- 所有考虑的因素组合成一个单实数指标不太容易,可设置满足指标和优化指标
- 例子:猫分类器
- 同时考虑准备率和运行时间
- 方案1:线性组合指标,\(cost=accuracy-0.5\times run_time\)。缺点:太刻意
- 方案2:能最大限度提高准确度,但必须满足运行时间要求。
- 优化指标:准确度,想尽可能的准确
- 满足指标:必须足够好,但是在达到足够好之后,不在乎到底有多好。比如100ms的运行时间是满足指标,那么80ms和95ms都是可以的。
- 所以这里,可以选择B分类器,在达到满足指标的情况下,优化指标是最好的

- N个指标:
- 1:设为优化指标,尽可能的优化
- N-1:设为满足指标,需要达到指定阈值
- 例子:语音设备的唤醒
- 准确性:说出唤醒词,多大概率唤醒设备。最大化准确性,【设为优化指标。】
- 假阳性:没说唤醒词,多大概率唤醒设备。满足24小时内最多1词假阳性唤醒,是可以接受的。【设为满足指标。】
训练集、开发集、测试集的分布
- 机器学习工作流程:
- 尝试很多思路
- 训练集训练不同的模型
- 用开发集评估不同的思路,从中选择一个,然后不断迭代改善开发集的性能,直到拿到一个满意的版本
- 用测试集取评估
- 例子:猫分类器,基于不同地区的数据如何划分数据?
- 前4个作为开发集,后4个作为测试集
- 结果:糟糕的,因为开发集和测试集来自不同的分布
- 开发集:设定瞄准的靶心(目标)
- 测试集:因为分布不同,其靶心不是上面已知尝试优化的靶心
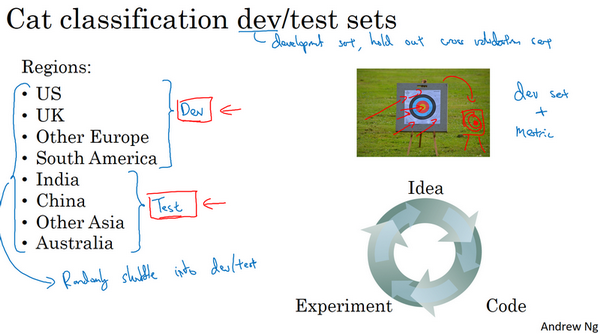
- 如何避免数据分布不同?
- 将所有数据随机洗牌,放入开发集和测试集。此时开发集和测试集都有来自不同地区的数据,并且来自同一分布(所有数据的混合)。
- 真实案例:
- 问题:输入x为贷款申请,输出y是否有还贷能力
- 开发集来自中等收入。基于此输出进行了优化。
- 在低收入的数据上进行一下测试。
开发集和测试集的大小
- 开发集和测试集必须来自同一分布,规模应该多大?
- 大小:
- 机器学习:
- 70/30比例分成训练集和测试集
- 60/20/20比例分成训练集、开发集和测试集
- 在数据集小的时候划分是合理的
- 深度学习:
- 数据集大得多
- 方案1:98/1/1的比例分成训练集、开发集和测试集。如果样本量是1000000,那么1%是10000,足够作为开发集和测试集。
-
方案2:小于20%或者30%的比例作为开发集和测试集
- 测试集大小:
- 如果需要足够的精确指标,可能需要百万数据作为测试集
- 如果不需置信度很高的评估,不需要那么大的测试集
-
测试集数量小于30%
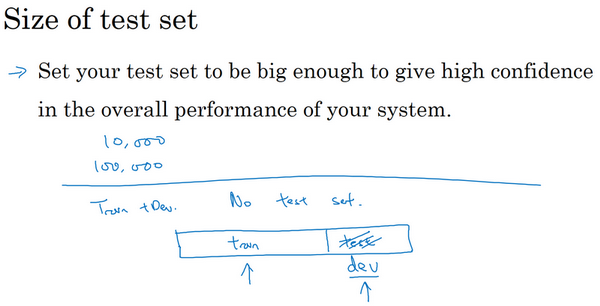
- 不建议省略测试集
- 单独的测试集:不带偏差的数据可以测量系统的性能
- 机器学习:
什么时候该改变开发集/测试集合评估指标?
- 如果项目进行途中,意识到出现了问题,可以采取一些措施进行模型修正,比如修开发集/测试集,或者评估指标
- 修改评估指标例子:
- 分类器:猫图像识别
- 算法A:错误率3%,算法B:错误率5%
- 部署:A某种原因把色情图像分类成猫,所以实际会也会给用户推荐一些色情图片。B错误率高,但是不会错误识别色情图片以作推荐。
- 评价指标+开发集 =》A更好
- 你+你的用户 =》B更好
- 原因:评价指标,也就是错误率的定义存在问题
- 错误率:对所有的图像,比较预测和真实值,算平均。但是这个是认为色情图片和非色情图片都是一样的。
- 做法:引入加权,再求和平均,对于色情图片,其权重可以设置很高,这样如果是色情图片,那么对应的会使得错误率加大。

- 如果评估指标无法正确评估好算法的排名,需要花时间定义一个新的评估指标
- 定义一个更好的指标,算是正交化的例子

- 修改开发测试集:
- 分类器:猫图像识别
- 算法A:错误率3%,算法B:错误率5%
- 部署:算法B效果更好
- 原因:手机用户的图片不是高质量的,而在训练和开发评估时,使用的都是高质量的数据。
- 做法:改变开发测试集,让数据更能反映实际需要处理的数据

为什么跟人的表现进行对比?
- 机器学习系统 vs 人类:
- 深度学习进步,机器学习算法效果更好了
- 机器做人的事情,工作流程效率更高
- 性能比较:
- 当研究一个问题一段时间,机器系统进展很快
- 当表现比人更好时,进展和精确度提升变慢
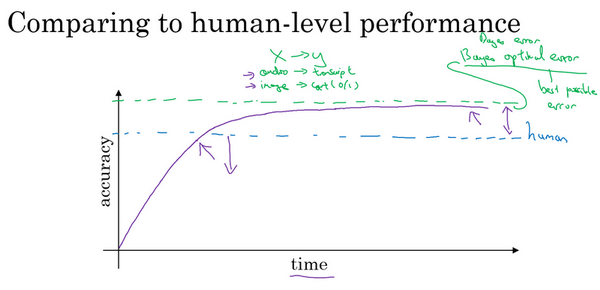
- 贝叶斯最优错误率:
- Bayes optimal error
- 模型越来越大,数据越来越多,但是性能无法超过某个理论上限
- 无论怎样,永远不会超过最优贝叶斯错误率(上面的紫线)
- 为什么超过人后进展变慢?
- 人类水平在很多任务上离最优错误率已经不远,当超越人后没有太多改善空间
- 当比人差时,有很多工具可以来提高性能,但是一旦超越人,这些工具没那么好用

可避免偏差

- 左边:
- 模型的训练集错误率8%,开发集错误率10%,人的错误率是1%,认为这个是接近于贝叶斯最优错误率的。
- 那么此时训练集拟合的并不好,因为训练误差还很大。
- 重点:减少偏差
- 右边:
- 模型的训练集错误率8%,开发集错误率10%,人的错误率是7.5%,认为这个是接近于贝叶斯最优错误率的。
- 那么此时训练集拟合的还可以,因为训练误差很接近于贝叶斯最优误差,虽然整体的错误率仍然是8%。所以模型表现只比人差一点点。
- 方差:训练集和开发集之间的差距,这里是2%,具有更多的改进空间。比如使用正则化或者搜集更多的训练数据,可以将方差减小。
- 可避免偏差:贝叶斯错误率的估计和训练错误率之间的差值。这里是0.5%
- 重点:减少方差
理解人的表现
- 什么是人类水平?
- 在医疗图片诊断中,不同的人会有不同的错误率,应该选择哪一种作为贝叶斯错误率的估计?

- 贝叶斯最优错误率应该是低于0.5%的,所以可以使用0.5%作为估计
- 实际部署中,也可使用其他的值,比如普通医生的1%作为贝叶斯错误率估计
- 在医疗图片诊断中,不同的人会有不同的错误率,应该选择哪一种作为贝叶斯错误率的估计?
- 例子:
- 医疗图像识别

- 左边:训练集错误率5%,开发集错误6%,贝叶斯错误率0.5%-1%。可避免偏差:4%-4.5%,方差:1%。偏差一定比方差大,所以重点是减少偏差(比如训练更大的网络)
- 中间:训练集错误率1%,开发集错误5%,贝叶斯错误率0.5%-1%。可避免偏差:4%-4.5%,方差:4%。方差一定比偏差大,所以重点是减少方差(比如正则化或者获取更大的数据集)
- 右边:
- 训练集错误率0.7%,开发集错误0.8%,贝叶斯错误率0.5%。可避免偏差:0.2%,方差:0.1%。可避免偏差更严重。
- 训练集错误率0.7%,开发集错误0.8%,贝叶斯错误率0.7%。可避免偏差:0%,方差:0.1%。方差更严重。
- 所以当你的模型效果越接近于人类时,取的进展会越来越难。
- 医疗图像识别
- 偏差和方差:
- 以前:比较训练错误率和0%,用这个估计偏差
- 现在:比较训练错误率和贝叶斯错误率,估计可避免偏差。

- 对人类水平有大概的估计可以让你做出对贝叶斯错误率的估计,更快的决定是否应该专注于减少算法的偏差或者方差。
超越人的表现
- 机器学习系统在接近或者超越人类水平的时候会变得越来越慢,为什么?
- 例子:
- 医疗图像识别
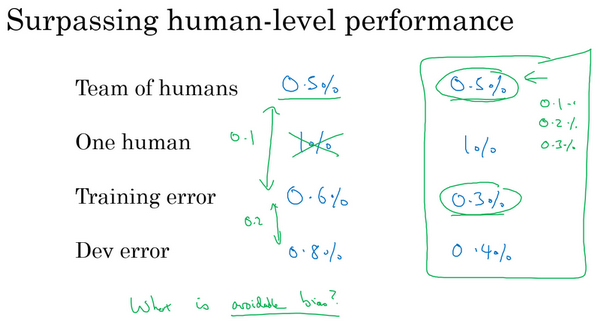
- 左边:训练集错误率0.6%,开发集错误0.8%。团队错误率0.5%,个人错误率1%。这里以0.5%作为贝叶斯错误率估计,那么可避免偏差是0.1%,方差是0.2%。所以减少方差空间更大。
- 右边:训练集错误率0.3%,开发集错误0.4%。团队错误率0.5%,个人错误率1%。
- 模型错误率比团队和个人的更低?模型错了?贝叶斯错误率其实是更低的(比如0.1%,0.2%)?
- 此时很难判断算法的优化方向到底是方差还是偏差了
- 没有明确的选项或者前进的方向
- 医疗图像识别
- 人:在自然感知任务中表现非常好
- 计算机:从结构化的数据中学习更具优势
- 广告点击
- 商品推荐等

改善模型表现
- 监督学习的两个本质假设:
- 对训练集拟合的很好,能做到可避免偏差很低。
- 推广到开发集和测试集也很好,就是方差不太大
- 如何提高模型效果:
- 降低可避免偏差:
- 更大的模型
- 训练更久
- 更好的优化算法
- 更好的网络、超参数:激活函数、层数、隐藏单元数等
- 。。。
- 降低方差:
- 收集更多数据
- 正则化:L2,dropout,数据增强
- 。。。
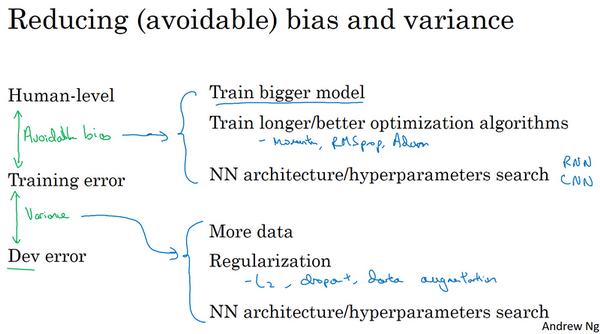
- 降低可避免偏差:
参考
Read full-text »
【2-3】深度学习的超参数优化、batch归一化
2019-02-05
目录
- 目录
- 调试过程
- 为超参数选择合适的范围
- 超参数调试:熊猫 vs 鱼子酱
- 归一化网络的激活函数
- Batch归一化拟合到神经网络中
- Batch归一化为什么有效?
- 测试时的batch归一化
- Softmax回归
- 训练一个softmax分类器
- 深度学习框架
- TensorFlow
- 参考
调试过程
- 超参数:
- 某些超参数比其他的更重要
- 【1】需调试的最重要的超参数:
- 学习速率
- 【2】仅次于\(\alpha\)的参数:
- Momentum参数\(\beta\):一般使用默认值0.9
- 隐藏单元的数目
- mini-batch size
- 【3】其他因素:
- 隐藏层数目
- 学习速率的衰减率
- 【4】最不重要
- Adam算法里面的参数:\(\beta_1, \beta_2, \varepsilon\),一般使用默认值:0.9,0.999,10^-8
- 如何选择超参数呢?
- 核心1:随机选择点,不要网格搜索
- 网格搜索:当参数的数量相对较少时,很实用
- 随机选择:深度学习领域推荐使用此方法
- 为啥随机搜索?
- 比如只有2个参数:学习速率\(\alpha\)和Adam参数\(\varepsilon\),显然前者比后者重要得多。
- 当选择同等数量的点进行调试时,【1】网格搜索:实验了5个不同的\(\alpha\),但是\(\varepsilon\)取任何值效果是一样的。【2】随机选择:可能取到了独立的25个\(\alpha\)值,就更可能发现选择哪一个更好。
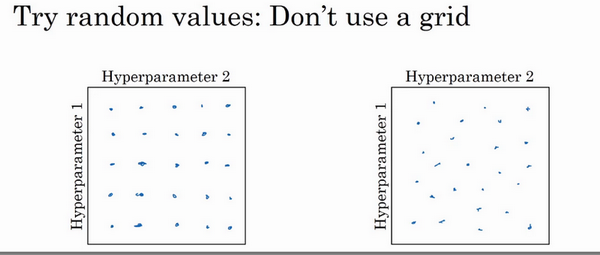
- 实际:三个甚至更多的超参数
-
随机取值而不是网格取值表明,你探究了更多重要的超参数的潜在值
- 核心2:由粗糙到精细的策略
- 比如在两个参数时,随机取了一些点,发现某个区域整体效果都还不错
- 接下来可以放大这块区域,然后更密集的随机取值
为超参数选择合适的范围
- 随机取值:
- 在超参数范围内可提升搜索效率
- 但不是均匀取值
- 而是选择合适的尺寸
- 有的参数可以随机(均匀)选取:
- 在范围内可以随机均匀选取
- 比如隐藏单元数目、层数

- 有的参数不能随机(均匀)选取:
- 不能线性的随机取
- 比如学习速率\(\alpha\):假设其范围是0.0001-1之间有最优,如果画一条范围直线随机均匀选取,则90%选取的值在0.1-1之间,10%在0.0001-0.1之间,这看上去是有问题的。
- 可用对数尺度去搜索:不使用线性的,依次取0.0001,0.001,0.01,0.1,1,然后在此对数数轴上均匀选取,这样资源才比较均等
- 具体:在\([10^a,10^b]\)之间取值,需要做的就是在[a,b]之间均匀取值(比如为r),然后取的超参数值=\(10^r\)
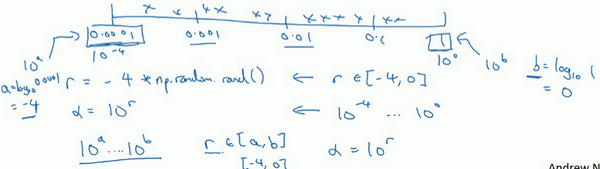
-
在对数坐标下取值,取最小的对数就得到a的值,取最大的对数就得到b值。在a,b间随意均匀的选取r值,再设置为\(10^r\)即可。
- 如何给Momentum的\(\beta\)取值?指数的加权平均
- 假如搜索区间是0.9-0.999
- 不能用线性轴,可探究\(1-\beta\)
- 当\(\beta:0.9-0.999\)时,\(1-\beta:0.1-0.001\),换为对数轴取值,在[-3,-1]之间均匀取值为r,然后超参数值\(1-\beta=10^r,\beta=1-10^r\)

超参数调试:熊猫 vs 鱼子酱
- 深度学习应用领域广泛,但是超参数的设定会随时间变化而变化,比如添加了新的数据等。建议:至少每隔几个月,重新测试或评估模型的超参数,以确保对数值已然很满意。
- 如何搜索超参数?
- 两种流派
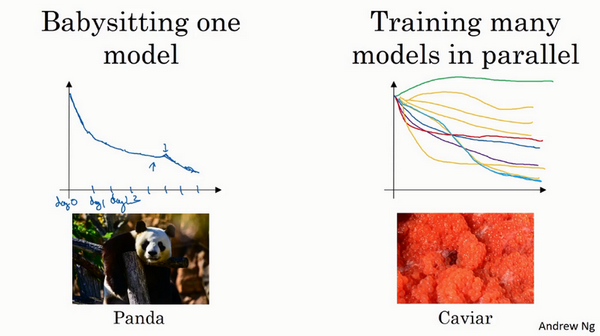
- 照看模式:随机化选择参数,一次实验一个,看效果。有的时候损失随着参数的更新一直在下降,突然某个时候可能又上升了。
- 熊猫方式:孩子很少,一次通常就一个
- 同时实验多种模型:平行实验许多不同的模型,最后快速选择效果最好的那个。
-
鱼子酱模式:繁殖的时候会产生很多卵
- 选择哪种?
- 取决于拥有的计算资源
- 如果足够多,选择鱼子酱模式
- 两种流派
归一化网络的激活函数
- Batch归一化
- 深度学习一个重要的算法
- 使得参数搜索问题变得容易
- 神经网络对超参数的选择更稳定
- 超参数的范围更庞大
- 特征值的归一化
- 特征值的归一化:减去平均值,除以方差
- 逻辑回归或者神经网络都可以用到这个
- 能加快学习过程
- 把学习的轮廓从很长的东西变成很圆的

- 激活值能否归一化?
- 对于更深的模型
- 特征值:输入层到第一个隐藏层
- 激活值:其他隐藏层之间的传递值,每一层的激活值a作为下一层的输入
- 试想:特征值的归一化是可以提高训练速度的,那么如果激活值也是归一化的,是不是也能提升训练速度呢?
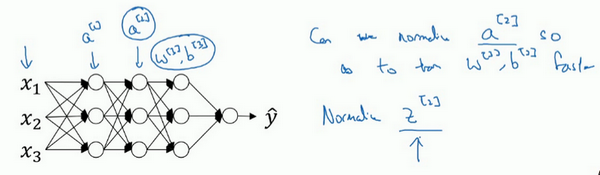
- z值的归一化:
- 我们通常选择归一化z,就是激活函数的输入值,而不是激活后的值【激活前z值的归一化】
-
把隐藏层的z值标准化,化为平均值为0和标准单位方差的值
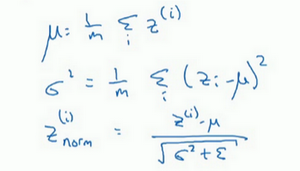
- 是否一定需要归一化为:均值为0,单位方差?
- 不一定!如果分布是有意义的,可以选择其他的值。
- 做法:不直接使用归一化的值,可以在归一化的值进行参数添加以控制,\(\widetilde{z}^{(i)} = \gamma z_{norm}^{(i)}+\beta\),这里控制的两个参数是需要进行设定的,就像Momentum里面的参数一样,也会在梯度下降中进行更新
-
可以看到,当满足:\(\gamma=sqrt(\sigma^2+\epsilon), \beta=\mu\)时,就是上面的均值为0,标准方差的归一化了
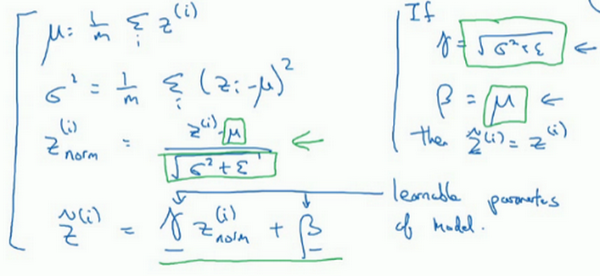
- 特征输入、隐藏单元区别:一般特征输入是归一化到平均值为0方差为1,但是隐藏神经元可以不一定是这个值,这一点就是通过引入的两个参数进行控制的
- 比如对于sigmoid函数,不像其归一化后的值总是在0附近,因为这样是趋于线性的
Batch归一化拟合到神经网络中
- Batch归一化是发生在计算
z和a之间的:- 输入层特征值通过与第一层之间的w、b参数,得到第一层的z
- 然后对z进行归一化,得到\(\widetilde{z}\)
- 对\(\widetilde{z}\)用激活函数计算a
- 以此类推
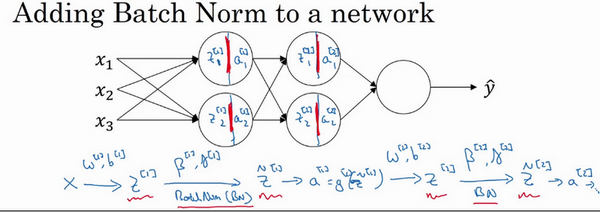
- 注意:这里每一层都是单独归一化的,所以每一层都有自己的参数:\(\\gamma, \beta\)
- Batch归一化通常和mini-batch一起使用
- 每一次对一个batch进行前向传播、归一化、反向传播、梯度下降等
- 参数b是被减去的:\(z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}\),归一化需要均值为0标准方差,再由参数\(\gamma, \beta\)进行缩放。所以\(b^{[l]}\)的值是被减去的。通过参数\(\beta^{[l]}\)进行控制,产生偏移或偏置。
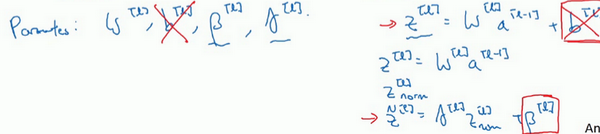
- 梯度下降更新:
- 对于batch归一化涉及的参数也要进行更新

- 对于batch归一化涉及的参数也要进行更新
Batch归一化为什么有效?
- 原因1:类比特征值归一化
- 做特征值归一化类似的工作,只不过对象是隐藏单元值
- 原因2:权重比网络更滞后或更深层
-
比如第10层的权重相比第1层的权重更能经受住变化(分布的变化等)
- 背景是:数据分布的变化对于网络使有影响的,需要重新许梿学习算法
- 例子:左边训练黑猫的模型,训练好了,现在应用于有色猫的识别
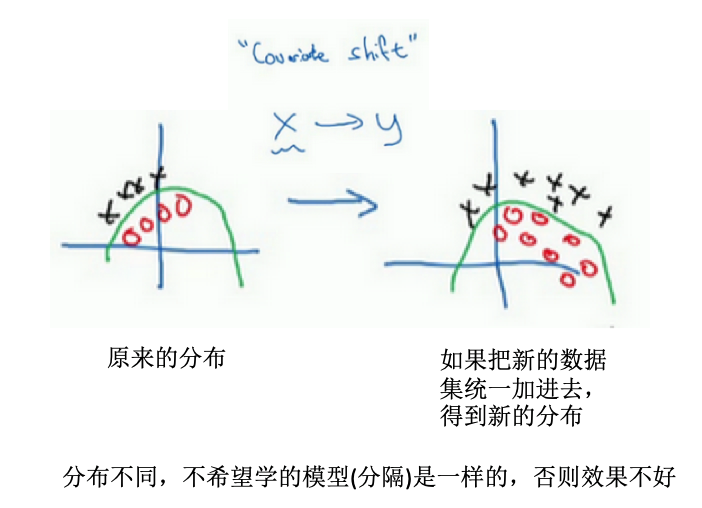
-
covariate shift:如果已经学习了x到y的映射,如果x的分布改变了,那么可能需要重新训练你的学习算法
- 为什么在神经网络中这是个问题?
- 某一层的激活值,在计算上直接与前一层的值有关,但是如果前面一些层的参数都发生了改变,那么这些隐藏单元的值也是在不断改变的,就有了上面的covariate shift问题
- batch归一化:减少隐藏值分布的变化,也许具体的z的值会变化,但是至少均值和方差分别是0和1.因此可以减少值的改变的问题,使这些值更加的稳定。
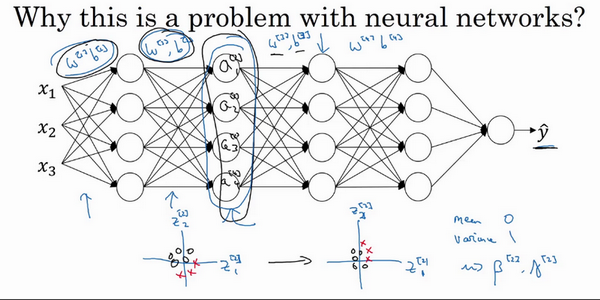
- 浅层不会左右移动那么多,因为被同样的均值和方差所限制,从而使得后层的学习更加容易。
-
- Batch归一化还有正则化的效果:
- 每个mini-batch上进行归一化,由均值和方差进行缩放
- 均值和方差是有一些噪声的:因为只是某一个mini-batch所计算出来的
- 结果:在隐藏层的激活值上增加了噪音。标准偏差的缩放和减去均值带来的额外噪音。
- dropout:也是增加噪音,隐藏单元以一定的概率乘以0或者1,应用较大的mini-batch可以减少正则化效果。
- 分析:标准偏差的缩放和减去均值带来的额外噪音。使得后部分的神经元不过度依赖于任何一个隐藏单元,所以有轻微的正则化效果。效果没有dropout那么强。

测试时的batch归一化
- 训练:以mini-batch的形式进行
- 测试:不能将一个mini-batch的样本同时处理,因为每次只是预测一个样本(此时均值和方差没有意义)。
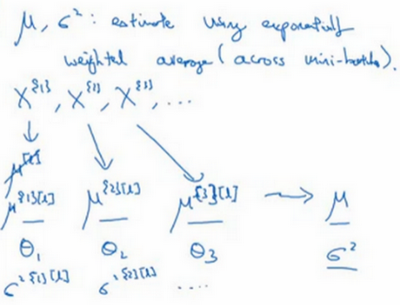
- 方法:为了将神经网络运用于测试,需要单独估算平均值和方差
- 原理:使用指数加权平均对均值和方差进行追踪,以计算指数加权平均值
- 具体:对于某一层l,有很多个mini-batch,每一个mini-batch都可以计算均值和方差。然后使用指数加权平均计算均值和方差,这个均值和方差就是在测试的时候用到的。
Softmax回归
- 二分类:标记是0和1
- softmax回归:
- 多分类的一种
- 不止识别两个分类
- 例子:
- 识别图片中的是猫、够、小鸡

- 输出:一个向量,表示了每一个类别的概率
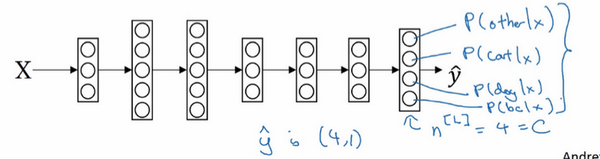
- 识别图片中的是猫、够、小鸡
- 为什么能做到多分类?
- softmax层+输出层实现
- softmax:对所有元素求幂,然后每个求幂元素的除以总的幂元素和(归一化),得到对应的幂指数数值的概率
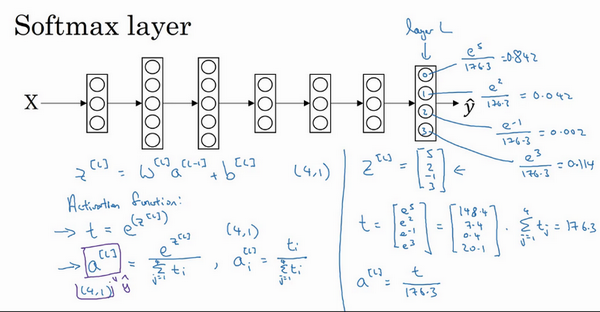
- 求幂指数概率的过程可看成是一个激活函数
- softmax激活函数:将所有可能的输出归一化,所以输入一个向量,输出也是一个向量,能够实现多分类
- softmax分类器:
- 还能干什么?实现多类的线性划分
- 例子:没有中间隐藏层的网络,输入层+softmax层+输出层
- 可以看到,当类别数=3时,一个softmax层可以实现线性决策边界的划分。同样的,对于其他能够两两之间线性分隔的,都可以在多分类的情况下被softmax分类器区分开来。
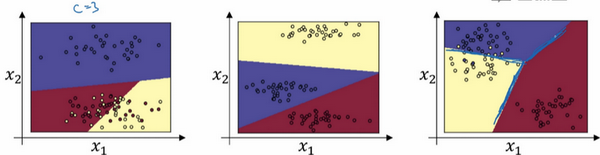
- 在类别数目C=5或者6的时候,也是可以实现的
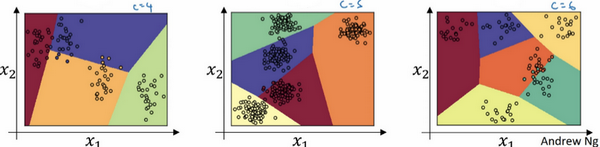
训练一个softmax分类器
- softmax vs hardmx:
- softmax: 指数归一化,输出的是概率向量,更为温和的映射
- hardmax:观察向量中的元素,最大的元素置为1,其他元素置为0.
- 比如下面,对于softamx计算出来的向量,对应的hardmax向量则是:[1 0 0 0]

- softmax回归 vs logistic回归:
- 前者是将逻辑回归的激活函数推广到C类
- 当C=2时,softmax实际上变回了逻辑回归

- 单个样本损失函数:
- 形式:\(L(\hat{y}, y)=-\sum_{i=1}^{10} y_l log{\hat{y}_j}\)
- 例子:如果真实标签是[0 1 0 0],表示一个猫的照片。输出向量 a=[0.3 0.2 0.1 0.4],从概率来看,在猫的概率值不是最大的,所以在这个样本的预测上效果不好。
- 直接从损失函数理解:因为y1,y3,y4都=0,只有y2=1,所以\(L(\hat{y}, y)=-y_2log(\hat{y}_2)=-log(\hat{y}_2)\),如果要损失函数越小,则对应的预测值\(\hat{y}_2\)应该越大越好,就是预测为第2类(猫)的概率值越大越好。
- 损失函数:找到训练集中的真实类别,然后使该类别相应的概率尽可能的高。
- 多样本的损失:
- 整个训练集损失的总和:
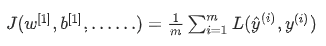
- 整个训练集损失的总和:
- 梯度下降最小化损失函数:
- 反向传播求导
- 导数:\(dz^{[l]}=\hat{y}-y)\),导数还是一个C维的向量
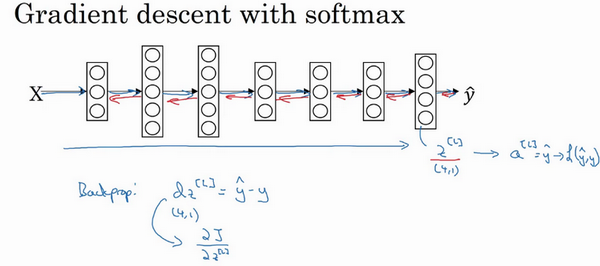
深度学习框架
- 从零开始实现模型不现实
- 框架:通过提供比数值线性代数库更高程度的抽象化,使得在开发深度学习应用时更加高效
- 如何选择框架:
- 便于编程
- 运行速度
- 真的是开源的,能有良好的管理

TensorFlow
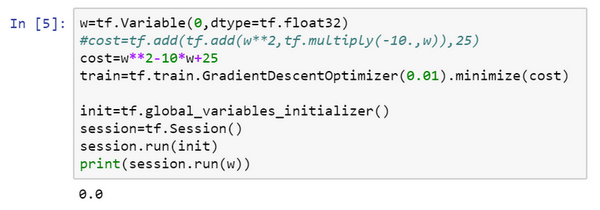
- 损失函数最小化:\(Jw=w^2-10w+25\)
import numpy as np
import tensorflow as tf
w = tf.Variable(0,dtype = tf.float32)
#接下来,让我们定义参数w,在TensorFlow中,你要用tf.Variable()来定义参数
#定义损失函数:
cost = tf.add(tf.add(w**2,tf.multiply(- 10.,w)),25)
# 使用梯度下降进行训练
#(让我们用0.01的学习率,目标是最小化损失)。
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
#最后下面的几行是惯用表达式:
init = tf.global_variables_initializer()
session = tf.Session() #这样就开启了一个TensorFlow session。
session.run(init) #来初始化全局变量。
#然后让TensorFlow评估一个变量,我们要用到:
session.run(w)
#上面的这一行将w初始化为0,并定义损失函数,我们定义train为学习算法,它用梯度下降法优化器使损失函数最小化,但实际上我们还没有运行学习算法
print(session.run(w))
# 0
session.run(train)
print(session.run(w))
# 0.1
for i in range(1000):
session.run(train)
print(session.run(w))
# 4.9999
# 结果很接近5了
- 定义cost函数的不同方式:
- 使用符号:add,multiply等
- 写公式:直接
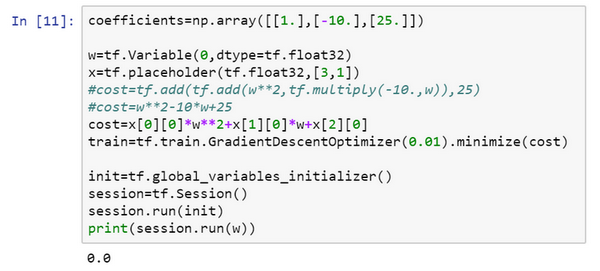
- placeholder:
- 之后会赋值的变量
- 告诉tf,会稍后为x提供数值
- 数据的占位:这里是对于损失函数的系数,直接使用一个向量x进行占位,所以在写损失函数的时候从x里面取值。然后再把定义的值feed到x
- 很方便的对更改系数值,相当于是一个函数了,比如把系数改为其他的值,那么此时最小化的是另外一个损失函数了,但是我们大体的代码是不便的。
- 使用with进行session的打开:
- 更方便清理
- 更常用

- tf核心:
- 计算损失函数,然后自动计算导数,及最小化损失
- 相当于建立计算图
- 通过计算损失,实现前向传播
- 不需要明确实现反向传播
参考
Read full-text »
【2-2】深度学习的算法优化
2019-02-02
目录
- 目录
- mini-batch梯度下降
- 理解mini-batch梯度下降?
- 指数加权平均
- 理解指数加权平均数
- 指数加权平均的偏差修正
- 动量梯度下降法
- RMSprop
- Adam优化算法
- 学习速率衰减
- 局部最优问题
- 参考
mini-batch梯度下降
- 优化算法:神经网络运行更快
- mini-batch vs batch:
- batch:对整个训练集执行梯度下降
- mini-batch:把训练集分割为小一点的子集,每次对其中一个子集执行梯度下降

- 比如有5000000个样本,每1000个样本作为一个子集,那么可得到5000个子集
- 用括号右上标表示:\(X^{\{1\}},...,X^{\{5000\}}\)
- 训练:
- 训练和之前的batch梯度下降一致,只不过现在的样本是在每一个子集上进行

-
对于每一个batch,前向传播计算,计算Z,A,损失函数,再反向传播,计算梯度,更新参数 =》 这是完成一个min-batch样本的操作,比如这里是1000个样本
- 遍历完所有的batch(这里是5000),就完成了一次所有样本的遍历,称为“一代”,也就是一个epoc
- batch:一次遍历训练集做一个梯度下降
- mini-batch:一次遍历训练集做batch-num个(这里是5000)梯度下降
- 运行会更快
- 训练和之前的batch梯度下降一致,只不过现在的样本是在每一个子集上进行
理解mini-batch梯度下降?
- 成本函数比较?
- 两者的成本函数如下:
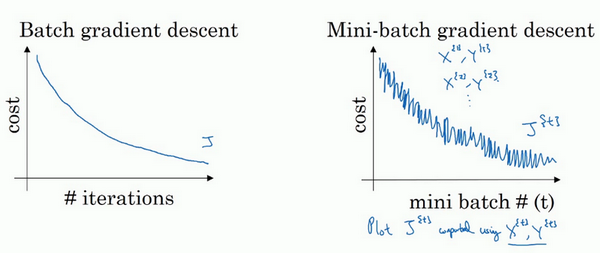
- 可以看到,整体的趋势都是随着迭代次数增加在不断降低的
- 但是batch情况下是单调下降的,而mini-batch则会出现波动性,有的mini-batch是上升的
- 为什么有的mini-batch是上升的?有的是比较难计算的min-batch,会导致成本变高(那为啥还要min-batch?因为快呀!!!)。
- 两者的成本函数如下:
- mini-batch size:
- 看两个极端情况
- size=m:batch梯度下降
-
size=1:随机梯度下降
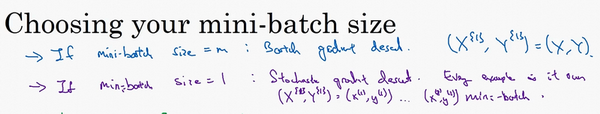
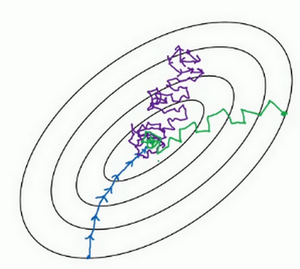
- 收敛情况不同:
- batch梯度下降:会收敛到最小,但是比较慢【蓝色】
- 随机梯度下降:不会收敛到最小,在最小附近波动【紫色】
-
合适的mini-batch梯度下降:较快的速度收敛到最小【绿色】
- 小训练集:m<2000,使用batch梯度下降即可
- 大训练集:mini-batch一般选为2的n次方的数目,比如64,128,256。64-512比较常见。
指数加权平均
- 还有一些比mini-batach梯度下降更快的算法
- 基础是指数加权平均
- 核心公式:\(v_t = \beta v_{t-1}+(1-\beta)\theta_t\)
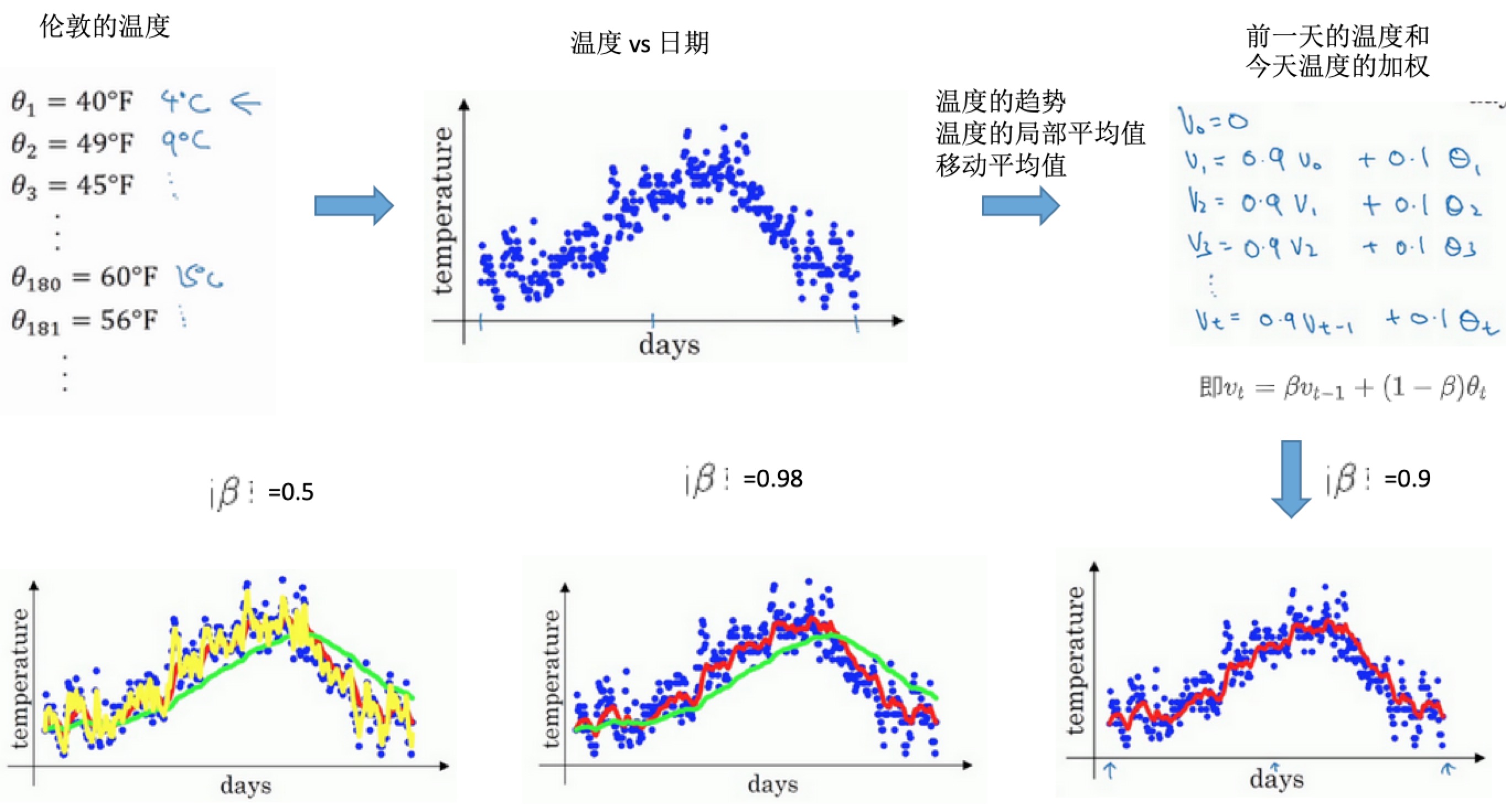
- 得到的是指数加权平均数
- 表示:大概是\(\frac{1}{1-\beta}\)天的平均温度
- 比如\(\beta=0.9\)时,是\(\frac{1}{1-0.9}=10\)天的平均值(上图红线部分)
- 比如\(\beta=0.98\)时,是\(\frac{1}{1-0.98}=50\)天的平均值(上图绿线部分)
- 因为是更多天的平均值,所以曲线波动小,更加平坦。
- 曲线向右移动,因为需要平均的温度值更多
- 如果温度变化,适应温度会更慢一点,出现延迟,因为前一天权重太大(0.98),当天温度权重太小(0.02)
- 比如\(\beta=0.5\)时,是\(\frac{1}{1-0.5}=2\)天的平均值(上图黄线部分)。平均数据较少,所以曲线有更多的噪声,有可能出现异常值。
理解指数加权平均数
- 加和平均的过程:
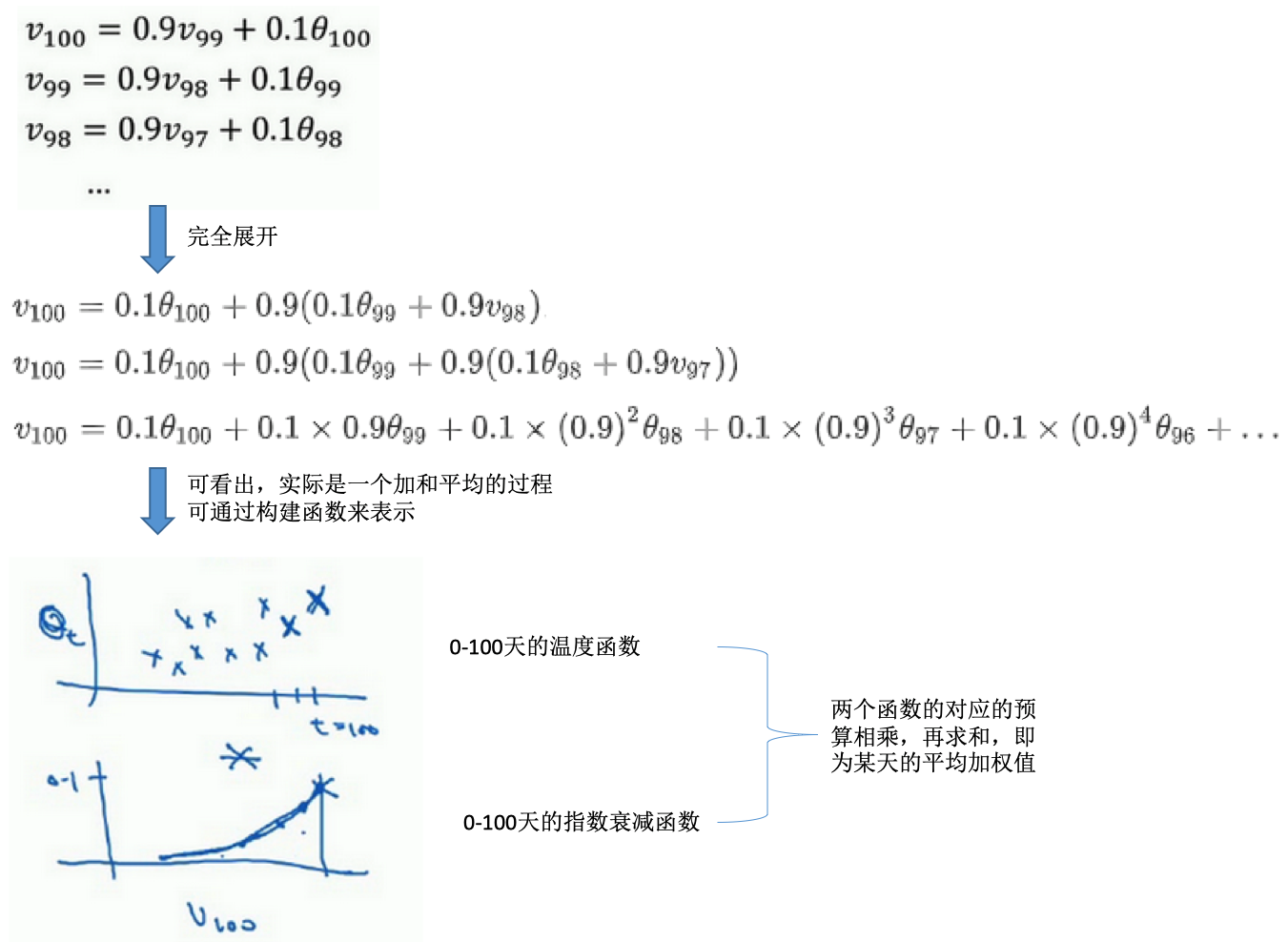
- 需要(表示)多少天的平均?
- 大概是\(\frac{1}{1-\beta}\)天的平均温度
- 如果\(\beta=0.9\)时,是\(\frac{1}{1-0.9}=10\)天的平均
- 此时,第10天0.9^10=0.35,约等于1/e(e是自然对数),也就是说10天后,曲线的高度下降到1/3,相当于峰值的1/e
- 实际计算:
- 一开始将\(V_0\)设置为0
- 再计算第一天\(v_1\),第二天\(v_2\)等。【所以第一天是等于\(1-\beta \theta\)温度值】
- 为什么指数加权平均?
- 占用极少内存
- 电脑中值占用一行数字,然后把最新的数据代入公式计算
- 一行代码
- 并不是最好或者最精确的计算平均数的方法
指数加权平均的偏差修正
- 偏差修正:让平均数的运算更加准确
- 修正策略:
- 主要是初期的估算不准确
- 在初期不直接使用Vt,而是除以了一个系数之后的值

- 所以当t比较大的时候,紫线和绿线会重合。偏差修正可以让在开始的阶段两者也能近似重合。
- 实际:不在乎执行偏差修正,宁愿熬过初始时期
动量梯度下降法
- 运行速度几乎总快于标准的梯度下降
- 基本思想:计算梯度的指数加权平均,利用这个梯度更新权重
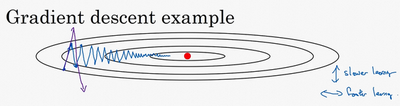
- 例子:
- 横轴希望能快速下降
- 纵轴希望较小波动
-
使用移动平均数,计算w和b的梯度,可减缓梯度下降的幅度

- 为什么这里梯度的移动平均是work的?
- 纵轴:导数上下晃动,但是摆动的平均值接近于0。所以取移动平均后,正负相互抵消,使得平均值接近于0。
- 横轴:所有的导数都是正方向的,所以平均后的值仍然很大。
- 最终:纵轴的摆动变小,横轴的运动更快,从而在抵达最小值的路上减小了摆动。
- 算法过程:
- 两参数:学习速率\(\alpha\)、参数\(\beta\)(控制着指数加权平均,常用值为0.9,相当于过去10此迭代的梯度的平均)
- 一般不会做偏差修正:10此迭代之后,移动平均已经过了初始阶段

RMSprop
- RMSprop:root mean square prop
- 加速梯度下降
- 在某次迭代:
- 计算w、b的梯度
- 计算指数加权的值,w、b的微分平方的指数加权平均
- 使用梯度除以上面的指数加权,进行梯度更新(不像momentum,直接使用微分的指数加权进行更新)
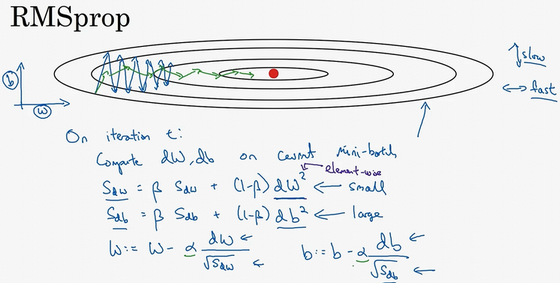
- 为什么有效果?
- 目标:水平方向(w方向),想保持大的梯度下降;竖直方向(b方向),想减缓摆动
- 如何做到:引入一个系数,就是原来的梯度除以一个系数
- 原来:\(W := W - \alpha dW, b := b - \alpha db\)
- 现在:\(W := W - \alpha \frac{dW}{sqrt(S_{dW})}, b := b - \alpha \frac{db}{sqrt(S_{db})}\)
- 水平w方向:斜率较小,所以dW较小
- 竖直b方向:斜率较大,所以db较大
- 结果:纵轴更新被一个大的数相除,消除摆动;水平更新则被小的数相除。在图中就是由蓝色的线变为绿色的线,纵轴摆动小,横轴继续推进。【核心:消除有摆动的方向,所以更快】
Adam优化算法
- 结合Momentum和RMSprop
- Adam:adaptive moment estimation,Adam权威算法
- 过程:
- 初始化
- 迭代时
- 先计算mini-batch的w、b的梯度
- 计算momentum指数加权平均,更新超参数\(\beta_1\)
- 计算RMSprop加权平均,更新超参数\(\beta_2\)
- 基于上述两者更新权重w和b
- 图解

- 超参数:
- 学习速率:\(\alpha\),需要调试
- dW的移动平均数:参数\(\beta_1\),momentum项,缺省值是0.9
- \((dW)^2,(db)^2\)的移动平均:参数\(\beta_2\),RMSprop项,推荐使用0.99
- 超参数\(epsilon\):选择没那么重要,建议是10^-8

学习速率衰减
- 随时间减少学习速率可加快学习算法
- 比较:
- 学习速率固定:蓝色线,整体会朝向最小值,但是不会精确收敛,因为mini-batch有噪声所以最后在最小值附近摆动
- 学习速率慢慢减小:绿色线,初期是学习速率较大,学习相对较快;随着学习速率的减小,会在最小值附近的一块区域摆动,而不是在训练中来回摆动。
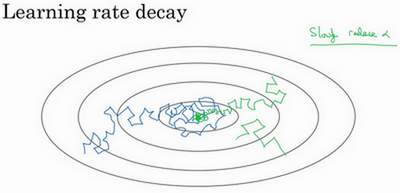
- 本质:学习初期,能承受较大的步伐;但当开始收敛的时候,小的学习速率能让步伐小一些。
- 如何设置:
- 设置为依赖于epoch的:\(\alpha=\frac{1}{1+decay_rate \times epoch_num}\)
-
decay_rate:需调整的超参数
- 例子:decay_rate=1, \(\alpha_0=0.2\)
- 第一代(epoch1):\(\frac{1}{1+1*1}\alpha_0=0.1\)
- 第二代:0.67
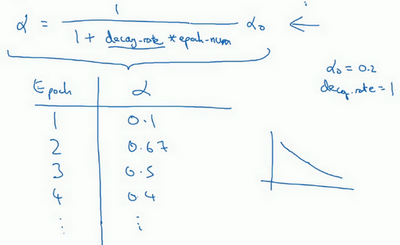
- 其他衰减函数:
- 指数衰减:epoch_num作为指数
- 离散下降:不同的阶段学习速率减小一半
- 手动衰减

局部最优问题
- 梯度为0通常不是局部最优,而是鞍点
- 高维空间概率局部最优概率很小:假设梯度为0,那么每个方向可能是凸函数,也可能是凹函数。要想是局部最优,需要每个方向都是凸函数,概率是2^(n),如果是高维空间,这个概率值很小。所以更可能碰到的是鞍点。
- 为什么叫鞍点?有一点导数为0.
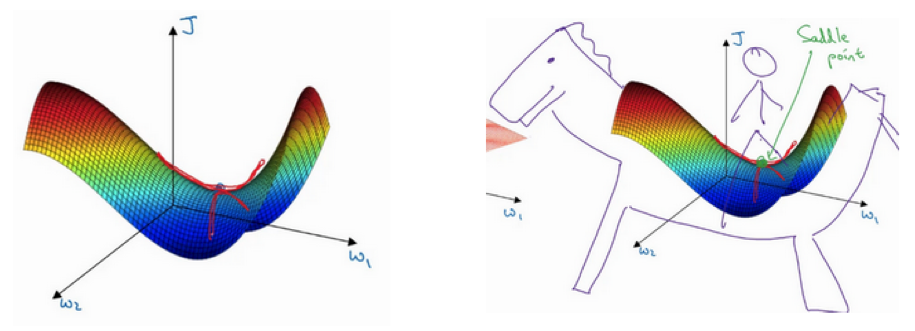
- 所以局部最优不是问题
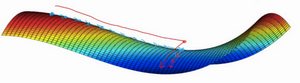
- 平稳段学习减缓:
- 局部最优不是问题
- 平稳段导数长时间接近于0,曲面很平坦
- 学习十分缓慢,这也是Momentum、RMSprop、Adam能加速学习的地方
- 需要很长的时间才能走出平稳段
参考
- 第二周:优化算法
- Sebastian Ruder: An overview of gradient descent optimization algorithms 一个比较不同的梯度下降优化算法的文章
Read full-text »
keras
2019-01-29
目录
概述
Keras: means horn in Greek。用python编写的,是高层的封装器,可以调用不同的后台,比如tensorflow,CNTK,Theano。目的就是为了更快的构建机器学习模型。
基本概念
基本的数据结构:model,构建网络层用的。最简单的模型是Sequential,线性堆叠的层。
构建模型
定义Sequential模型:
from keras.models import Sequential
model = Sequential()
添加层.add():
from keras.layers import Dense
model.add(Dense(units=64, activation='relu', input_dim=100))
model.add(Dense(units=10, activation='softmax'))
keras的一个核心就是Dense函数,用于构建全连接层,其实现的操作是output = activation(dot(input, kernel) + bias),全部参数如下:
keras.layers.Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)
- units: 正整数,输出空间维度[不是输入]。
- activation: 激活函数。若不指定,则不使用激活函数 (即,「线性」激活: a(x) = x)。
- use_bias: 布尔值,该层是否使用偏置向量。
- kernel_initializer: kernel 权值矩阵的初始化器。
- bias_initializer: 偏置向量的初始化器.
- kernel_regularizer: 运用到 kernel 权值矩阵的正则化函数。
- bias_regularizer: 运用到偏置项的的正则化函数。
- activity_regularizer: 运用到层的输出的正则化函数 (它的 “activation”)。
- kernel_constraint: 运用到 kernel 权值矩阵的约束函数。
- bias_constraint: 运用到偏置向量的约束函数。
使用例子,第一层显示指定输入的大小尺寸,必须和feed的数据的feature数目相同,否则无法导入数据:
# 作为 Sequential 模型的第一层
model = Sequential()
model.add(Dense(32, input_shape=(16,)))
# 现在模型就会以尺寸为 (*, 16) 的数组作为输入,
# 其输出数组的尺寸为 (*, 32)
# 在第一层之后,你就不再需要指定输入的尺寸了:
model.add(Dense(32))
编译模型
基于网络编译模型.compile(),编译模型函数.compile()包含3个参数:
- 优化器(optimizer):已定义的优化器名称或者类对象
- 损失函数(loss):已定义的损失函数名称或者自定义的损失函数
- 指标列表(metric):对于分类问题,一般设为
[accuracy]
model.compile(loss='categorical_crossentropy',
optimizer='sgd',
metrics=['accuracy'])
在构建模型时刻自定义loss函数,优化函数的参数等:
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.SGD(lr=0.01, momentum=0.9, nesterov=True))
训练模型
# x_train and y_train are Numpy arrays --just like in the Scikit-Learn API.
model.fit(x_train, y_train, epochs=5, batch_size=32)
# 手动batch训练
model.train_on_batch(x_batch, y_batch)
评估模型
loss_and_metrics = model.evaluate(x_test, y_test, batch_size=128)
预测新数据:
classes = model.predict(x_test, batch_size=128)
示例:Multilayer Perceptron (MLP) for multi-class softmax classification
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.optimizers import SGD
# Generate dummy data
import numpy as np
x_train = np.random.random((1000, 20))
y_train = keras.utils.to_categorical(np.random.randint(10, size=(1000, 1)), num_classes=10)
x_test = np.random.random((100, 20))
y_test = keras.utils.to_categorical(np.random.randint(10, size=(100, 1)), num_classes=10)
model = Sequential()
# Dense(64) is a fully-connected layer with 64 hidden units.
# in the first layer, you must specify the expected input data shape:
# here, 20-dimensional vectors.
model.add(Dense(64, activation='relu', input_dim=20))
model.add(Dropout(0.5))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss='categorical_crossentropy',
optimizer=sgd,
metrics=['accuracy'])
model.fit(x_train, y_train,
epochs=20,
batch_size=128)
score = model.evaluate(x_test, y_test, batch_size=128)
cheatsheet
参考
- keras @ github
- Getting started with the Keras Sequential model
- 快速开始序贯(Sequential)模型
- keras-cheat-sheet
Read full-text »
【2-1】深度学习的实践层面:数据集、正则化、梯度
2019-01-27
目录
- 目录
- 数据集:训练、验证、测试集
- 偏差和方差
- 偏差方差应对
- 正则化
- 正则化为什么可减少过拟合?
- dropout正则化
- 为什么dropout有用?
- 其他正则化方法
- 归一化输入
- 梯度消失/爆炸
- 神经网络权重初始化
- 梯度的数值逼近:双链误差更准确
- 梯度检验
- 参考
数据集:训练、验证、测试集
- 训练神经网络时的一些决策:
- 多少层
- 每层的隐层单元的数目
- 学习速率选择多少
- 每层采用什么激活函数
- 高度迭代的过程:
- 想法:不同的参数设置等
- 编程
- 运行查看结果
- 基于结构完善,提出新的想法
- 最佳决策取决于:
- 数据量
- 计算机配置中输入特征的数量
- GPU还是CPU进行训练
- 项目进度的关键:
- 循环迭代过程的效率
- 一个可行的方案:创建高质量的训练、验证和测试数据集
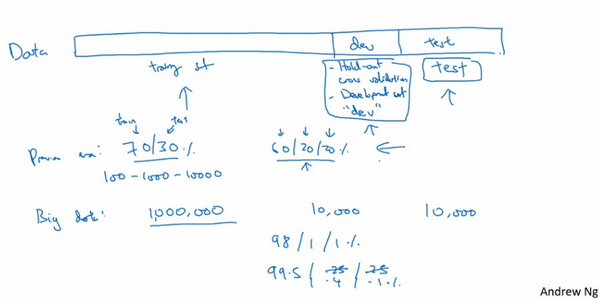
- 数据集划分:
- 流程:对训练集执行算法,通过验证集选择最好的模型,经过验证后,选定最好的模型。在测试集上进行评估,为了无偏评估算法的运行状况。 * 训练集
- 验证集
-
测试集
- 小数据量:
- 常见:三七分,70%训练集,30%测试集
- 最近认可的:60%训练集,20%验证集,20%测试集
- 数据量:100,1000或者10000条,划分是合理的
- 大数据量:
- 验证+测试:倾向于比例更小
- 验证集:检测哪种算法更有效,不需要20%的数据作为验证集
- 数据量:比如百万级别
- 100万数据:1万验证,1万测试 =》98%训练集,1%验证集,1%测试集
- 超过百万的:训练集99.5%,验证测试各0.25%,或者验证0.4%测试0.1%即可
- 训练和测试集不匹配:
- 深度学习的趋势
- 不匹配是指数据来源不匹配,导导致数据分布不匹配
- 不是正负样本失衡这种
- 验证集和测试集最好来自同一个分布
- 测试集要不要?
- 测试集目的:对最终选定的神经网络系统做出无偏估计
- 如果不需要无偏估计,可以不设置测试集
- 只有训练集+验证集:训练集训练,尝试不同模型,验证集评估,迭代选出最合适的即可。因为验证集已涵盖测试集数据,不再提供无偏估计。
偏差和方差
- 机器学习:偏差和方差易学难精
- 深度学习:对偏差和方差的权衡研究很浅
- 二维例子:
- 高偏差:直线拟合,不能很好的拟合数据,出现高偏差,也是欠拟合
- 高方差:复杂神经网络拟合,但是数据过度拟合,即过拟合
- 复杂程度适中的分类器
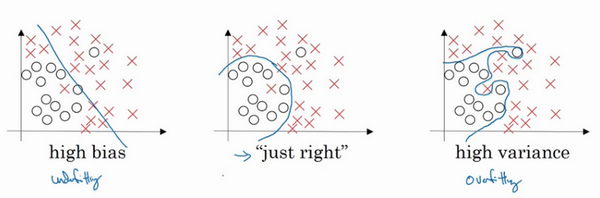
- 这里是二维特征,可可视化研究,现实中的高维,如何判断?不同的指标
指标:训练集误差和验证集误差

- 训练集误差1%,验证集误差11%:训练很好,验证相对差,可能是模型过度拟合训练集,验证集没有利用其交叉验证的作用 =》 高方差
- 训练集误差15%,验证集误差16%:训练数据拟合度不高,是欠拟合的 =》 高偏差。在验证集上的结果是合理的,因为和训练误差相差不大。
- 训练集误差15%,验证集误差30%:训练数据拟合度不高,同时在验证集上效果也很差 =》 高偏差+高方差
-
训练集误差0.5%,验证集误差1%:效果很好,偏差和方差都很低。
- 例子:
- 直线:高偏差(拟合效果差)
- 中间扭曲、两端直线:高偏差+高方差,高偏差因为其整体还是直线,区分效果差;高方差是因为中间拟合对了两个样本【有些区域偏差大,有些区域方差大】
- 二次曲线:效果挺好
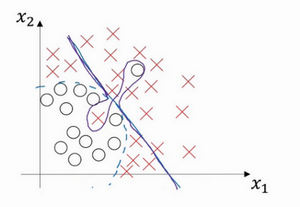
偏差方差应对
- 偏差高:
- 一般是看训练集,也同时看一下验证集效果
- 方案:选择新模型,更多层,更多隐藏单元,更先进的优化算法,延长训练时间
- 最低标准:不断尝试上面的方法,消除偏差问题,直到可以拟合数据,至少是拟合训练集数据
- 方差高:
- 一般是验证集上的性能查看方差大小
- 方案:更多的数据、正则化
- 注意:
- 高偏差和高方差是不同的。比如是高偏差问题,增多数据也没多少用处。
- 偏差和方差权衡。机器学习阶段讨论较多,因为有较多的方法,深度学习则不然。
正则化
- 过拟合(高偏差):
- 更多数据:可靠但是成本太高
- 正则化:减少网络误差,避免过拟合
- 范数:
- 关于范数的介绍可参考这里:几种范数的简单介绍
- L0范数:向量x中非零元素的个数
- L1范数:\(\|\|x\|\|_1=\sum_i\|x_i\|\),非零元素的绝对值之和。也称为“稀疏规则算子”。
- L2范数:\(\|\|x\|\|_2=\sqrt{\sum_ix_i^2}\),元素的平方和再开方。也称为“岭回归”或者“权重衰减”。
- L-∞范数:\(\|\|x\|\|_\infty=max(\|x_i\|)\),向量元素的最大值
- 线性回归正则化:
- L1正则化:Lasso回归
- L2正则化:Ridge回归(岭回归)
- 逻辑回归正则化:
- L1正则化:w最终会是稀疏的,很多值是0。间接实现特征选择,适合于特征有关联的情况。
- L2正则化:很多w接近于0,使得优化求解稳定快速,适合特征间没有关联的情况。使用的是范数平方。

- 神经网络正则化:
- 正则化:范数平方
- 正则化矩阵范数称为“弗罗贝尼乌斯范数”,用F标注:其实使用的是L2范数
- 矩阵中所有元素的平方和
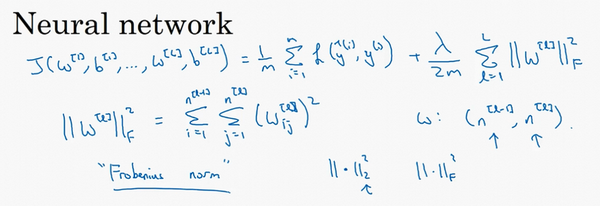
- 加入正则化后的权重衰减:
正则化为什么可减少过拟合?
- 基于网络神经元的理解:
- 如果开始是过拟合(高方差)的状态:
- 当\(\lambda\)很大,权重会接近于0,可理解为很多隐藏神经元权重设置为0,这部分神经元会被消除。整个网络变为一个很简单的网络,小到如同一个神经元,但是深度很大,此时会从过拟合转变为左边的欠拟合(高偏差)的状态。
- 当\(\lambda\)取值合适,能得到一个中间的状态。
- 直观理解:很多神经元的权重会很低,这些神经元对于网络的影响很小,整个的神经网络变得简单,所以不容易发生过拟合。
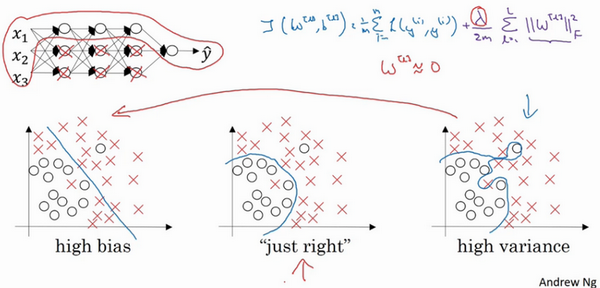
- 基于激活函数的理解:
- 如果\(\lambda\)很大,整体损失很小,那么权重w很小
- 权重很小时,z也会很小
- 如果z的范围很小,比如都在靠近0的地方,那么当激活函数是tanh的时候,g(z)大致是线性的
- 每层都是线性的话,就和线性回归函数类似
- 线性网络,不是一个极复杂的非线性函数,从而不会发生过拟合

- 这里列举了一些关于正则化L1/L2的原理、为什么有效果、不同的模型中有何效果的问题,可以参考一下。
dropout正则化
- dropout正则化:
- 随机失活
- 非常实用
- 遍历网络的每一层,设置消除神经网络结点的概率
- 设置完成后,会消除一些结点及对应结点的连线,从而得到一个更小规模的网络,在进行反向传播训练
- 例子:
- 如何实现dropout?
- 常见:反向随机失活(inverted dropout)
- 阈值参数:
keep-prob,表示隐藏单元保留的概率 - 对于每一层的节点,随机生一个和节点数目相等的向量,然后比较每个位置的数值与上面的阈值的大小,如果高于这个阈值,此节点设置为1(保留),否则设置为0(消除)。得到一个
判断向量。 - 然后
激活函数 = 激活函数x判断向量,这样更新后的激活函数值,就可以把判断为0(消除)的节点的数值元素归为0. - 最后
激活函数=激活函数/keep-prob,得到修正后的激活函数值,因为此时的激活函数值是要作为下一层的输入的,如果不想改变下一层的期望值,就需要进行弥补操作。比如第3层50个节点,80%概率保留,\(z^4=w^4a^3+b^4\),其中\(a^3\)减少了20%(有20%元素被归为0),为了不影响\(z^4\)期望(或者说确保\(a^3\)的期望不变),需要\(w^4a^3/0.8\)以弥补所需的20%。
- 在测试阶段,不需要使用dropout
为什么dropout有用?
- 基于特征权重的理解:
- 不依赖于任何特征,因为其输入随时可能被清除
- 权重会比较均匀的传播下去,能达到权重收缩的平方范数的效果
- 类似于L2正则化

- 设置方案1:参数keep-prob:
- 表示每一层上保留单元的概率
- 不同的层可以变化
- 有的层节点较多,过拟合可能严重,可以设置较小的值
- 有的层节点较少,过拟合不严重,可以把该值设置的高一些
- 如果某层不担心过拟合,可以设置为1
- 此时的设置有点像L2正则化中的\(\lambda\)
- 缺点:搜索更多的超参数
- 设置方案2:
- 某些层应用dropout,某些层不使用
- dropout:
- 计算机视觉:用的多,输入量很大,输入太多像素,没有足够的数据,容易过拟合
- 只是一种正则化方法,有助于预防过拟合
- 除非算法过拟合,不然不使用
- 缺点:代价函数J不再被明确定义
其他正则化方法
- 已介绍:
- L2正则化
- dropout
- 还有:
- 数据扩增
- 动物识别:可以水平翻转,裁剪等操作
- 光学字符:添加数字,随意扭曲或旋转
- 这种方式比较廉价
- early stop
- 绘制训练和验证误差
- 一般训练集误差随着迭代次数进行一直下降
- 验证集误差刚开始是下降的,在某个点后开始上升
- 找到这个中间点,然后停止迭代
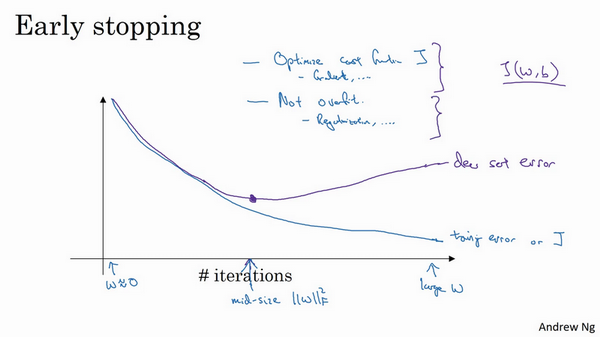
- 优点:只运行一次梯度下降,,可以找出w的较小值、中间值和较大值,无需尝试L2正则化参数\(\lambda\)的很多值
- 数据扩增
归一化输入
- 加速训练:归一化输入
- 【1】零均值:求特征的均值,x减去对应的均值。是移动数据集的操作,直到完成零均值化。
- 【2】归一化方差:求每个特征方差\(\sigma^2\),数据除以方差。
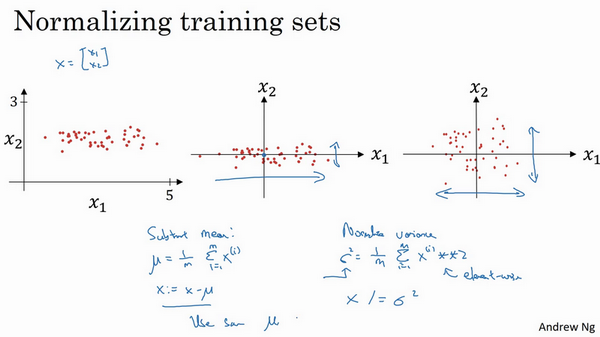
- 注意:
- 用训练集相同的均值和方差去归一化测试集
- 不能在训练集和测试集上分别预估均值和方差
- 为什么要归一化?
- 当不同的特征值范围差异很大时,代价函数不是圆的
- 当特征值都在相近的范围,代价函数会更容易优化
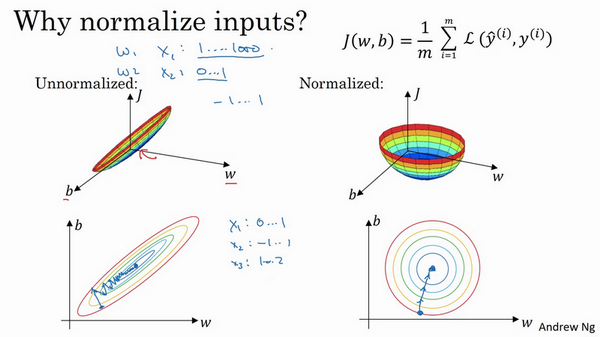
- 执行归一化不会产生危害,通常会做归一化处理
梯度消失/爆炸
- 梯度消失或爆炸:
- 训练神经网络的时候,导数有时会变得非常大或者非常小,甚至以指数方式变小,加大了训练的难度
- 例子:
- 一个多层,每层两个结点的神经网络
- 激活函数:g(z)=z,线性激活函数
- 忽略b
- 输入x,输出y:\(y=W^{[l]}W^{[l-1]}W^{[l-2]}...W^{[2]}W^{[1]}x\)
- 如果每个权重w一样,且\(w^{[l]}=\begin{bmatrix}1.5 & 0 \\0 & 1.5\end{bmatrix}\),这个是1.5倍的单位矩阵,\(\hat y = 1.5^{(L-1)}x\),是呈指数级增长的,y的值将爆炸式增长
- 如果权重是0.5,即\(w^{[l]}=\begin{bmatrix}0.5 & 0 \\0 & 0.5\end{bmatrix}\),它比1小,\(\hat y = 0.5^{(L-1)}x\),激活函数将以指数级下降
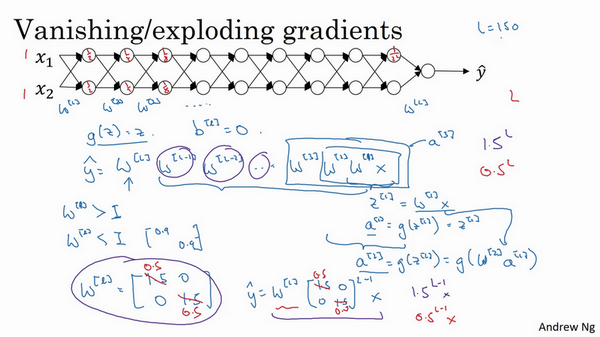
- 权重W只比1(单位矩阵)略大一点,深度神经网络的激活函数将爆炸式增长;如果比1略小一点,深度神经网络的激活函数将指数级递减。【这个问题其实不太理解,即使后面说初始化权重,但是也不等于1,也是比1大一点的或者小一点的,不是也会出现爆炸或者消消失吗?】
神经网络权重初始化
- 梯度爆炸或消失解决方案:权重初始化(谨慎的设置初始权重),能部分解决问题
- 单个神经元例子:
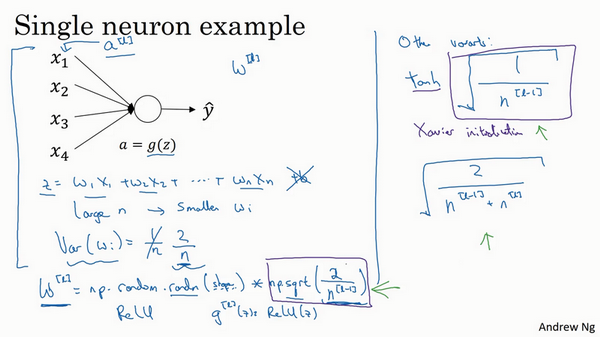
- z是x和权重的线性组合
- 为了预防z过大或过小,如果n越大,希望w越小。最理想的是w=1/n
- 如果选择了ReLU激活函数,方差设置为2/n效果更好
- 还有其他的一些变体,告诉我们当选择不同的激活函数时,初始化的权重应该是怎么样的效果比较好
梯度的数值逼近:双链误差更准确
梯度检验
- 对于所有的参数构建一个大的向量
- 利用双边误差估计对于每个参数的导数
- 反向传播计算的导数
- 注意:
- 不要在训练中使用,只用于调试
- 如果梯度检验失败(有的不符合),需检查所有项,尝试找出问题
- 如果有正则化,在进行梯度检验时也要考虑
- 梯度检验与dropout不能同时使用
- 当w,b都接近于0时,梯度下降的实施是正确的。所以可以随机初始化使得w、b的值接近于0.
参考
Read full-text »
【1-4】深层神经网络
2019-01-23
目录
深层神经网络
- 前面:一个隐藏层的神经网络,正向传播,反向传播,向量化,随机初始化权重
- 逻辑回归:一层的神经网络
- 有一个隐藏层的神经网络,就是一个两层神经网络。输入层不算。
- 层数:\(L\)表示
- \(L\)层激活后结果:\(a^{[l]}\),正向传播需要计算的就是这个;激活函数:\(g\),其输入是\(z^{[l]}\)
- 符号表示参见指南
前向和反向传播
- 前向:计算Z(基于上一层的输出),再计算a(激活后)
- 反向:根据当前层对a的导数,计算上一层对啊的导数,以及当前层对参数w和b的导数

深度网络中的前向传播
- 一个训练样本:
- 计算第一层z,再激活后的a
- 计算第二层z,再激活后的a
- 。。。
- 计算第四层z,再激活后的a。此时的a就是最后的输出,因为第四层就是输出层了。
- 一个样本(向量化实现):
- 计算Z:\(Z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}\)
- 计算激活后的a:\(A^{[l]}=g^{[l]}(Z^{[l]})(A^{[0]}=X)\)
核对矩阵的维数
- 常用检查代码方法:
- 过一遍算法中矩阵的维数
- 参数w维度:(下一层维数,前一层维数),\(w^{[l]}:(n^{[l]},n^{[l-1]})\)
- 参数b维度:(下一层维数,1),\(w^{[l]}:(n^{[l]},1)\)
- z和激活后a的维度:\(z^{[l]},a^{[l]}:(n^{[l]},1)\)。输出值是下一层的结点数目。
为什么使用深层表示?
- 神经网络不一定很大,但是需要有深度,就是有比较多的隐藏层,为什么?
- 例子:
- 人脸识别系统
- 前面的几层是简单的探测,比如不同的层探测人脸不同的部位如眼睛边缘、鼻子侧翼等
-
后面的层则可以探测更复杂的函数,比如眼睛、鼻子等
- 语音识别
- 前几层:音频波形特征,音调高低、噪声、简单的丝丝声音等
- 后几层:声音的基本单元、单词、句子等
- 层次递进:
- 较早的几层:学习低层次的简单特征
-
后几层:把简单的特征组合起来,探测更复杂的东西
- small:隐藏单元的数量相对较少
- deep:隐藏层数目比较多
- 如果浅层网络要表达深层同样的效果,需要指数级增长的单元数目才行
- 电路理论:
- 不同的基本逻辑门
- 比如计算异或或者奇偶性
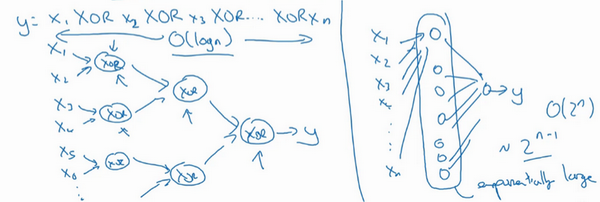
- 异或树:或门+非门,树图的网络深度:\(O(log(n))\),节点的数量和电路部件(门的数量)并不会很大
- 浅层:比如单隐藏层,列举耗尽2^n种可能,需要的隐藏单元数是\(O(2^n)\)
搭建神经网络模块
- 正向步骤:正向函数
- 反向步骤:反向函数
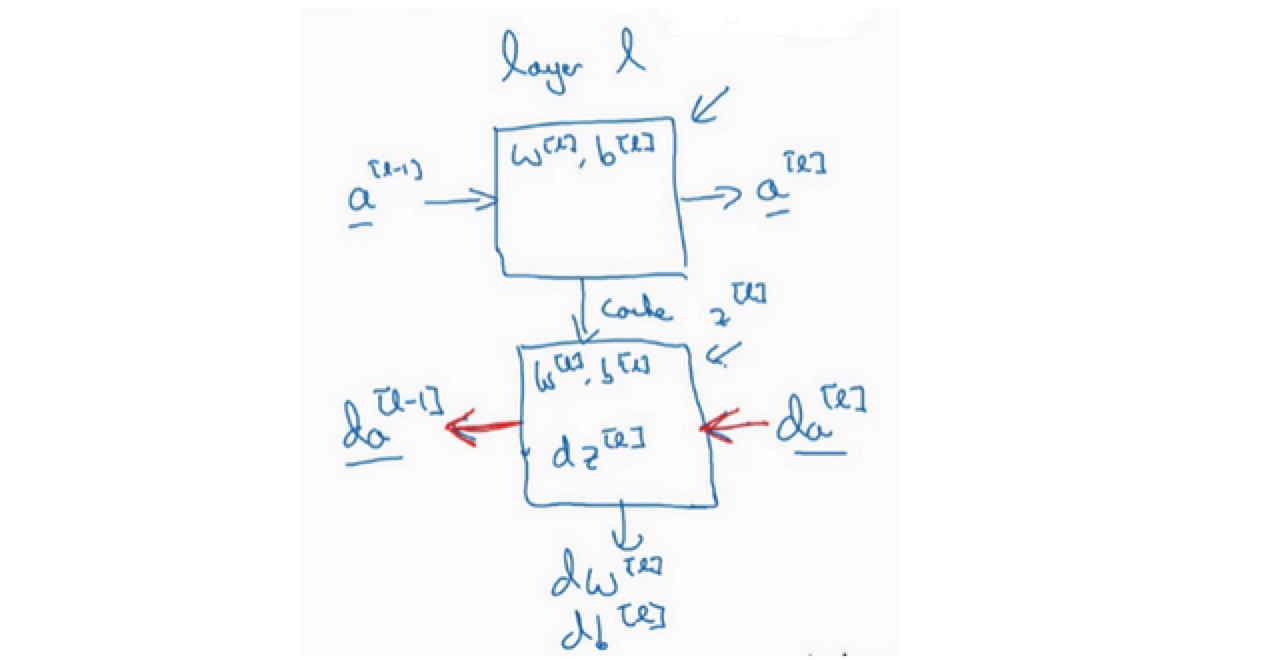
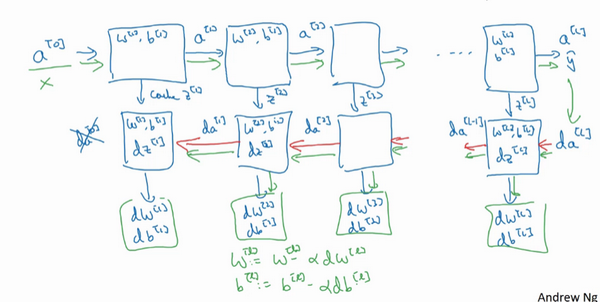
- 一步训练:
- 前向:从\(a^{[0]}\)开始,通过正向传播计算得到\(\hat y\)
- 反向:用输出值\(\hat y\)计算导数,从最后开始计算。得到:所有的导数项,同时,W和b在每一层也会更新
参数vs超参数
- 超参数:
-
控制了最后的其他的参数w和b的值,所以称为超参数
- 常见的一些超参数包含:
- 学习速率
- 梯度下降法循环的次数
- 隐藏层数目
- 隐藏层单元数目
- 激活函数
- momentum
- min batch size
- 正则化参数
-
- 寻找最优超参数:
- 尝试不同的参数,实现模型并观察是否成功,然后再迭代
- 偏于经验性
- 必须尝试很多次不同的可能性(深度学习令人不满的一部分)
- 有一条经验规律:经常试试不同的超参数,勤于检查结果,看看有没有更好的超参数取值,你将会得到设定超参数的直觉。
参考
Read full-text »
Latest articles
Links
- ZhangLab , RISE database , THU life , THU info
- Data analysis: pandas , numpy , scipy
- ML/DL: sklearn , sklearn(中文) , pytorch
- Visualization: seaborn , matplotlib , gallery
- Github: me





